Matières
Niveaux
Dans l'animation suivante, tu peux modifier les paramètres |a,| |b,| |c,| |h| et |k| de la fonction exponentielle et observer leurs effets sur les propriétés de la fonction. Après cette exploration, tu pourras poursuivre la lecture de la fiche pour connaitre toutes les précisions concernant les propriétés de la fonction.
| Propriétés | Fonction exponentielle de base | Fonction exponentielle en forme canonique |
|---|---|---|
|
Règle |
||f(x)=c^x|| Asymptote en |y=0| |
||f(x)= ac^{b(x-h)}+k|| Asymptote en |y=k| |
|
Domaine |
|\mathbb{R}| ou selon le contexte. |
|\mathbb{R}| ou selon le contexte. |
|
Image |
Les images sont définies dans l'intervalle |]0,+\infty[.| |
Si |a>0| et |b>0,| les images sont définies dans l'intervalle |]k,+\infty[.| Si |a<0| et |b>0,| les images sont définies dans l'intervalle |]-\infty,k[.| |
|
Zéro de la fonction |
|\forall x,\ f(x)\neq 0| |
Existe si |a>0| et |k<0| ou |a<0| et |k>0.| S'il existe un zéro, c'est la valeur de |x| |
|
Signe de la fonction |
Avec |c>0| et |c\neq 1,| la fonction est positive sur tout son domaine. |
Selon l'équation de la fonction et l'existence du zéro. |
|
Ordonnée à l'origine |
Si |x=0,| alors |f(x)=1.| |
C'est la valeur de |f(x)| lorsque |x=0.| |
|
Extrémums |
Aucun ou selon le contexte. |
Aucun ou selon le contexte. |
|
Croissance |
Si |c>1,| la fonction est croissante sur son domaine. |
Si |c>1| et que |a| et |b| sont Si |0<c<1| et que |a| et |b| sont de |
|
Décroissance |
Si |0<c<1,| la fonction est décroissante sur son domaine. |
Si |0<c<1| et que |a| et |b| sont Si |c>1| et que |a| et |b| sont |
Déterminez les différentes propriétés de la fonction |f(x)=-2 (3)^{x+1}+3.|
Il est très utile de tracer un graphique afin de s'aider.
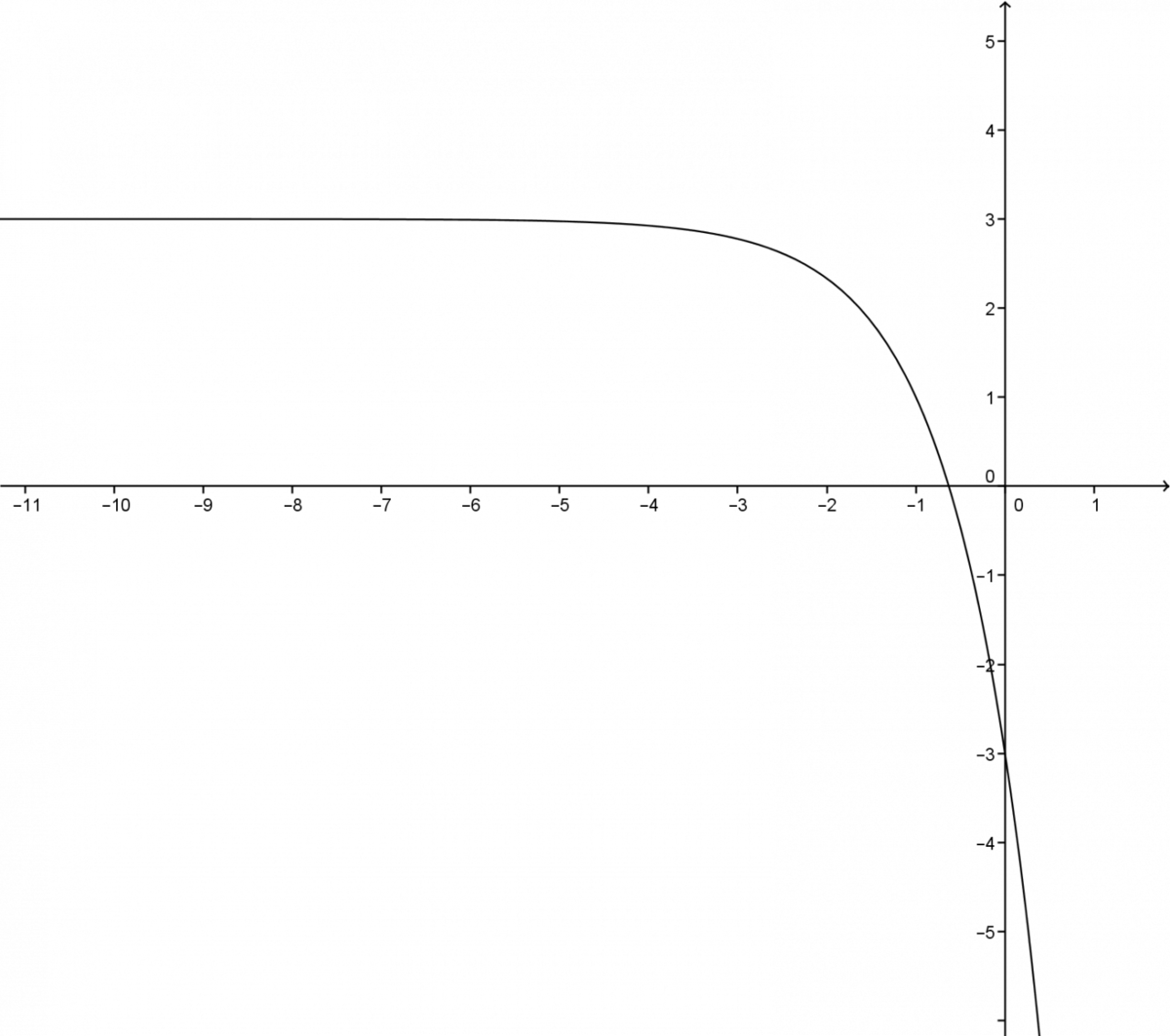
L'asymptote de cette fonction est |y=3.|
Le domaine de la fonction est l'ensemble des nombres réels qu'on note |\mathbb{R}.|
L'image de la fonction est l'intervalle |]-\infty, 3[.|
Le zéro de la fonction se calcule en remplaçant |f(x)| par |0| et en isolant |x.| ||\begin{align} 0 &= -2 (3)^{x+1}+3\\-3 &= -2 (3)^{x+1}\\ 1{,}5 &= 3^{x+1}\end{align}||Rendu ici, on passe à la forme logarithmique. ||\begin{align}\log_3 1{,}5 &= x+1\\ \log_3 1{,}5 - 1 &= x\\ -0{,}63 &\approx x\end{align}||Donc, le zéro vaut environ |-0{,}63.|
Le signe de la fonction est positif lorsque |x| appartient à l'intervalle |]-\infty;-0{,}63]| et il est négatif lorsque |x| appartient à l'intervalle |[-0{,}63; +\infty[.|
Pour calculer l'ordonnée à l'origine, on remplace |x| par |0.| ||\begin{align}f(0) &= -2 (3)^{0+1} + 3\\ f(0) &= -3\end{align}||L'ordonnée à l'origine de la fonction est |-3.|
La fonction n'a aucun extrémum.
La variation : la fonction est décroissante. En effet, |c>1,| puis |a| et |b| sont de signes contraires.