Matières
Niveaux
Pour accentuer l'effet de profondeur des images et des solides, les projections centrales sont idéales.
Une projection centrale correspond à la représentation d'un objet en trois dimensions respectant la ligne d'horizon (identifiée par un ou des points de fuite) et la position de cet objet dans l'espace par rapport au point d'observation.
Le grand avantage de la projection centrale est qu'elle permet de représenter un solide sur papier avec énormément de réalisme. Dans ce type de projection, la ligne d'horizon et la position de l'objet dans l'espace par rapport à la position de l'observateur sont respectées. En d'autres mots, plus l'objet est éloigné de l'observateur, plus il est petit.
La projection centrale est étroitement liée à l'homothétie où le point de fuite joue le rôle de centre d'homothétie. Certaines faces étant proportionnelles, il est possible de déduire des mesures sur une projection centrale grâce au rapport d'homothétie ou au rapport de similitude.
Dans cette perspective, les arêtes qui définissent la profondeur d'un solide convergent vers un point de fuite situé sur la ligne d'horizon. Ainsi, la face représentée dans le plan frontal n'est pas déformée par rapport à la réalité, mais les autres le sont toutes.
Tracer la base voulue dans le plan frontal et le point de fuite.
Tracer les lignes fuyantes.
Tracer la base la plus éloignée.
Compléter le solide.
Trace la projection centrale d'un prisme à base trapézoïdale selon une perspective à un point de fuite.
Pour bien voir l'impact du point de fuite sur le résultat final, tu peux le sélectionner et le déplacer.
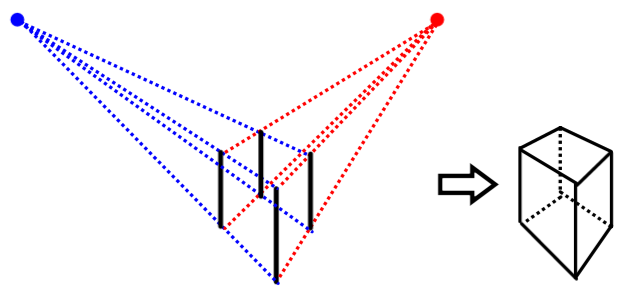
Dans une perspective à deux points de fuite, les arêtes associées à une dimension du solide convergent vers un point de fuite situé sur la ligne d'horizon, et les arêtes associées à une autre dimension convergent vers un autre point de fuite situé sur la même ligne d'horizon.
Tracer un premier point de repère
Tracer les lignes fuyantes
Tracer d'autres arêtes verticales
Tracer les autres lignes fuyantes
Tracer la dernière arête verticale
Compléter le solide
Tracer un premier point de repère
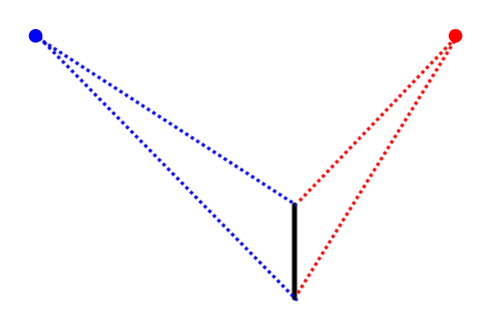
Dans ce cas, il s'agit de tracer l'arête verticale du solide qui est la plus près de l'observateur. De plus, les deux points de fuite peuvent être fournis ou tracés arbitrairement. Dans un cas comme dans l'autre, ils doivent absolument être sur une même ligne horizontale puisqu'ils définissent l'horizon.

Tracer les lignes fuyantes
Tracer des lignes fuyantes joignant les points de fuite à chaque extrémité de l'arête verticale.
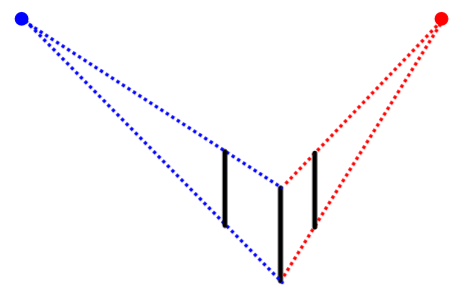
Tracer d'autres arêtes verticales
Tracer deux arêtes verticales parallèles à celle déjà tracée en respectant les limites des lignes fuyantes.
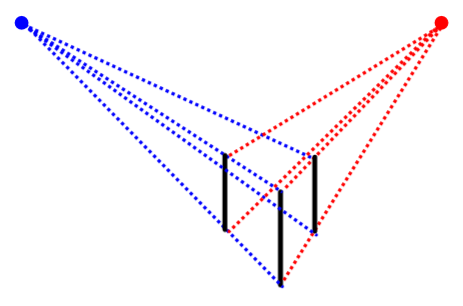
Tracer les autres lignes fuyantes
Tracer des lignes fuyantes joignant les points de fuite à chaque extrémité des nouvelles arêtes verticales.
Tracer la dernière arête verticale
Tracer l'arête la plus éloignée de l'observateur, soit celle formée par l'intersection des nouvelles lignes fuyantes, en respectant les limites des lignes fuyantes et le parallélisme avec les autres arêtes verticales.
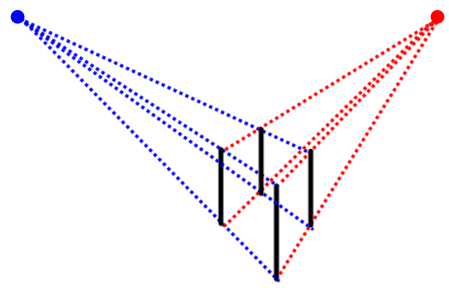
Compléter le solide
Tracer le solide en enlevant les lignes fuyantes inutiles et en prenant soin d'utiliser le pointillé pour identifier les arêtes qui ne sont pas visibles dans la réalité.