Matières
Niveaux
Une expérience aléatoire est une expérience dont le résultat dépend entièrement du hasard et dont les résultats possibles sont connus.

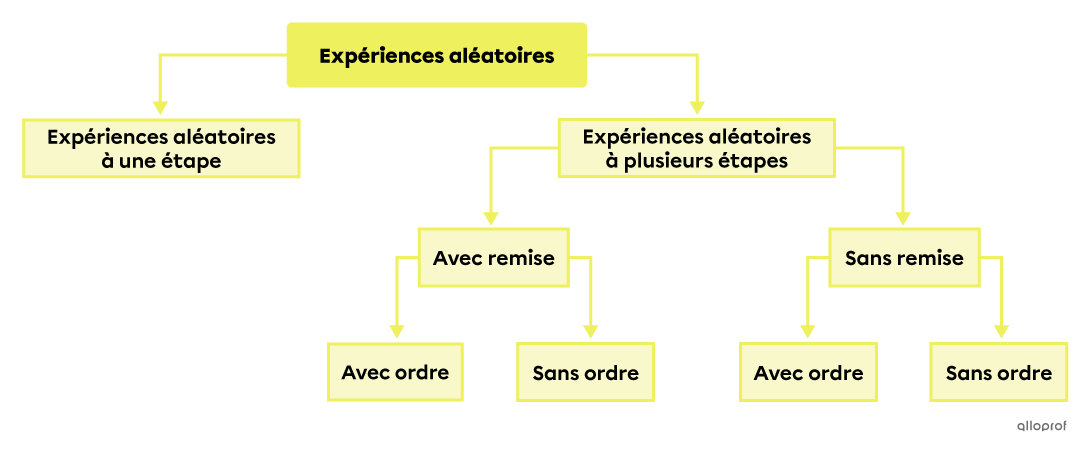
Il existe plusieurs types d’expériences aléatoires. Pour dénombrer et calculer des probabilités, il est important d'identifier à quel type de cas correspond le problème en se posant 3 questions.
L’expérience comporte-t-elle plusieurs étapes?
S’il y a plusieurs étapes, est-ce que les expériences sont avec ou sans remise?
S’il y a plusieurs étapes, est-ce qu’on doit tenir compte ou non de l’ordre des résultats?
L'univers des résultats possibles d'une expérience aléatoire à une étape, aussi appelée expérience aléatoire simple, est formé par l'énumération entre accolades de tous les résultats qu'il est possible d'obtenir. Dans ce cas, la probabilité d'un évènement s'exprime par le rapport entre le nombre de résultats favorables et le nombre de résultats possibles.
Si on pige une bille dans un sac contenant |3| billes vertes, |2| billes rouges et |1| bille bleue, quelle est la probabilité de piger une bille verte?
Il y a |3| résultats favorables (|3| billes vertes) sur un total de |6| résultats possibles (les |6| billes dans le sac).||\begin{align}P(\text{bille verte})&=\dfrac{\text{Nombre de résultats favorables}}{\text{Nombre de résultats possibles}}\\&=\dfrac{3}{6}\end{align}||
Réponse : La probabilité de piger une bille verte est de |\dfrac{3}{6},| soit |\dfrac{1}{2}.|
Lorsqu'un évènement est composé de plusieurs résultats favorables (évènement |A| ou évènement |B|), il suffit d'additionner la probabilité de chaque résultat pour déterminer la probabilité de l'évènement.
Si on pige une bille dans un sac contenant |3| billes vertes, |2| billes rouges et |1| bille bleue, quelle est la probabilité de piger une bille verte ou une bille rouge?
Il y a |5| résultats favorables (|3| billes vertes et |2| billes rouges) sur un total de |6| résultats possibles.||\begin{align}P(\text{bille verte ou rouge})&=\dfrac{\text{Nombre de résultats favorables}}{\text{Nombre de résultats possibles}}\\&=\dfrac{3+2}{6}\\&=\dfrac{5}{6}\end{align}||
Réponse : La probabilité de piger une bille verte ou une bille rouge est de |\dfrac{5}{6}.|
La somme des probabilités de tous les évènements élémentaires lors d'une expérience aléatoire à une étape est égale à |1.|
On pige une bille dans un sac qui contient |3| billes vertes, |2| billes rouges et |1| bille bleue. Les |3| évènements élémentaires sont : « piger une bille verte », « piger une bille rouge » et « piger une bille bleue ».
||\begin{align}P(\text{verte})&=\dfrac{3}{6}\\P(\text{rouge})&=\dfrac{2}{6}\\P(\text{bleue})&=\dfrac{1}{6}\\\end{align}||Si on additionne les probabilités des évènements élémentaires, on obtient bel et bien |1.|||\begin{align}P(\text{verte})+P(\text{rouge})+P(\text{bleue})&=\dfrac{3}{6}+\dfrac{2}{6}+\dfrac{1}{6}\\&=\dfrac{6}{6}\\&=1\end{align}||
Une expérience aléatoire à plusieurs étapes, aussi appelée expérience aléatoire composée, est une série d’expériences aléatoires réalisées une à la suite de l’autre.
Pour dénombrer les résultats possibles lors d'une expérience aléatoire à plusieurs étapes, il est parfois suffisant de multiplier le nombre de résultats possibles à chacune des étapes. C’est ce qu’on appelle le principe multiplicatif.
|\begin{gathered}\text{Nombre de}\\\text{résultats}\\\text{possibles}\end{gathered}=\begin{gathered}\text{Nombre de}\\\text{choix à}\\\text{l'étape 1}\end{gathered}\times\begin{gathered}\text{Nombre de}\\\text{choix à}\\\text{l'étape 2}\end{gathered}\times\ \dots|
Pour calculer des probabilités d'une expérience aléatoire à plusieurs étapes, il suffit de multiplier les probabilités des différents choix qui nous intéressent à chacune des étapes. Il s’agit aussi du principe multiplicatif.
|P(A\ \text{suivi de}\ B)=P(A)\times P(B)|
où
|P(A):| probabilité du 1er évènement
|P(B):| probabilité du 2e évènement
Le code postal canadien est constitué de chiffres (C) et de lettres (L) dans l’ordre suivant : LCL CLC.
Les lettres D, F, I, O, Q et U ne sont pas utilisées.
Les lettres W et Z sont utilisées, mais jamais en 1re position.
Postes Canada, dont le code postal est K1A 0B1, estime qu’il y a actuellement |800\ 000| codes postaux utilisés au Canada. Quel pourcentage du nombre total de codes postaux possibles cela représente-t-il?

Lors d’une expérience aléatoire à plusieurs étapes, il faut toujours se demander s’il s’agit d’une expérience avec ou sans remise et s’il s’agit d’une expérience avec ou sans ordre.
On lance un dé à |6| faces |2| fois de suite. Quelle est la probabilité d'obtenir un |3| suivi d'un |4|?
Un lancer de dé est considéré comme une expérience avec remise, puisqu’au 2e lancer, les |6| options sont encore possibles. Comme on veut un |3| suivi d’un |4,| on doit tenir compte de l’ordre.
La probabilité d'obtenir un |3| au 1er tirage est de |\dfrac{1}{6}| et la probabilité d'obtenir un |4| au 2e tirage est aussi de |\dfrac{1}{6}.| On doit multiplier les probabilités de chaque choix pour obtenir la probabilité de l'évènement.||P(\text{3 suivi d'un 4})=\dfrac{1}{6}\times \dfrac{1}{6} = \dfrac{1}{36}||
Réponse : La probabilité d’obtenir un |3| suivi d’un |4| est de |\dfrac{1}{36}.|
On pige |3| cartes dans un jeu de 52 cartes, sans remettre les cartes pigées dans le jeu. Quelle est la probabilité d'obtenir, dans l'ordre, |2| cartes rouges et une carte noire?
La probabilité d'obtenir une carte rouge au 1er tirage est de |\dfrac{26}{52},| soit |\dfrac{1}{2}.| Comme c’est une expérience sans remise, la probabilité d'obtenir une carte rouge au 2e tirage est de |\dfrac{25}{51}.| La probabilité d'obtenir une carte noire au dernier tirage est de |\dfrac{26}{50},| soit |\dfrac{13}{25}.| On doit multiplier les probabilités de chaque étape pour obtenir la probabilité de l'évènement.||P(R,R,N)=\dfrac{1}{2}\times \dfrac{25}{51}\times \dfrac{13}{25} = \dfrac{13}{102}||
Réponse : La probabilité d’obtenir |2| cartes rouges suivies d’une carte noire est de |\dfrac{13}{102}.|
