Matières
Niveaux
Diverses opérations mathématiques peuvent être effectuées sur les matrices:
L'addition et la soustraction de matrices ne sont possibles que lorsque les deux matrices sont de mêmes dimensions, c'est-à-dire qu'elles ont le même nombre de lignes et le même nombre de colonnes.
Pour additionner deux matrices, il suffit d'additionner les éléments occupant les mêmes positions dans chaque matrice. La somme obtenue est une nouvelle matrice.
L'addition de deux matrices suit donc le modèle suivant:
|A+B=\begin{pmatrix}
a & b\\
c & d
\end{pmatrix} +\begin{pmatrix}
e & f\\
g & h
\end{pmatrix}=\begin{pmatrix}
a+e & b+f\\
c+g & d+h
\end{pmatrix}=C|
Si on additionne les matrices |A| et |B| suivantes:
|A+B=\begin{pmatrix}
6 & 5 & 4\\
4 & 3 & 5
\end{pmatrix}+\begin{pmatrix}
3 & 4 & 2\\
4 & 4 & 3
\end{pmatrix}=\begin{pmatrix}
6+3 & 5+4 & 4+2\\
4+4 & 3+4 & 5+3
\end{pmatrix}|
On obtient donc la nouvelle matrice |C|:
|\begin{pmatrix}
6 & 5 & 4\\
4 & 3 & 5
\end{pmatrix}+\begin{pmatrix}
3 & 4 & 2\\
4 & 4 & 3
\end{pmatrix}=\begin{pmatrix}
9 & 9 & 6\\
8 & 7 & 8
\end{pmatrix}=C|
Pour soustraire deux matrices, il suffit de soustraire aux éléments de la première matrice les éléments occupant la même position dans la deuxième matrice. Il est aussi possible d'additionner l'opposé de la deuxième matrice à la première matrice plutôt que de la soustraire. Tout comme dans l'addition, la soustraction de deux matrices résulte en une nouvelle matrice.
La soustraction de deux matrices suit donc le modèle suivant:
|A-B=\begin{pmatrix}
a & b\\
c & d
\end{pmatrix} -\begin{pmatrix}
e & f\\
g & h
\end{pmatrix}=\begin{pmatrix}
a-e & b-f\\
c-g & d-h
\end{pmatrix}=C|
Si on soustrait la matrice |B| de la matrice |A| dans l'exemple ci-dessous:
|A-B=\begin{pmatrix}
3 & 4 & 4\\
5 & 4 & 6
\end{pmatrix}-\begin{pmatrix}
2 & 5 & 1\\
6 & 4 & 4
\end{pmatrix}=\begin{pmatrix}
3-2 & 4-5 & 4-1\\
5-6 & 4-4 & 6-4
\end{pmatrix}=C|
On obtient donc la nouvelle matrice C:
|A-B=\begin{pmatrix}
3 & 4 & 4\\
5 & 4 & 6
\end{pmatrix}-\begin{pmatrix}
2 & 5 & 1\\
6 & 4 & 4
\end{pmatrix}=\begin{pmatrix}
1 & -1 & 3\\
-1 & 0 & 2
\end{pmatrix}=C|
Pour multiplier une matrice par un scalaire, il faut multiplier chaque élément de la matrice par ce scalaire. Le produit obtenu est donc une nouvelle matrice.
La multiplication d'une matrice par un scalaire suit donc le modèle suivant:
|k\times\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}=\begin{pmatrix}
ka & kb\\
kc & kd
\end{pmatrix}|
|4\times\begin{pmatrix}
1 & 5 & 2\\
-1 & 7 & -3
\end{pmatrix}=\begin{pmatrix}
4 & 20 & 8\\
-4 & 28 & -12
\end{pmatrix}|
Le produit d'une matrice |A| par une matrice |B| est possible si et seulement si le nombre de colonnes de la matrice |A| est égal au nombre de lignes de la matrice |B|.
Le produit obtenu lors de la multiplication de deux matrices est une nouvelle matrice |C|.
Soit la multiplication de matrices suivantes:
|A_{m\times p}\times B_{p\times n}=C_{m\times n}|
La nouvelle matrice possède donc le même nombre de lignes que la matrice |A| et le même nombre de colonnes que la matrice |B|.
Pour déterminer un élément de la matrice |C|, il faut:
Voici un schéma représentant le cas de deux matrices |3 \times 3|:
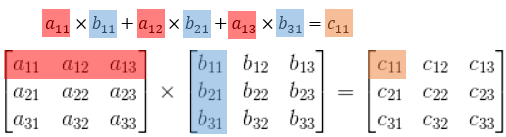
1. On multiplie dans l'ordre, élément par élément, chaque élément d'une ligne de la première matrice |A| par chaque élément d'une colonne de la deuxième matrice |B| et ce, pour l'ensemble des éléments des deux matrices.
|\small A \times B=\begin{pmatrix}
{\color{Blue} 1} & {\color{Blue} 2}\\
{\color{Red} 0} & {\color{Red} 4}\\
3 & -1
\end{pmatrix}\times\begin{pmatrix}
{\color{Magenta} 2} & {\color{DarkGreen} 0}\\
{\color{Magenta} 1} & {\color{DarkGreen} -3}
\end{pmatrix}=\begin{pmatrix}
{\color{Blue} 1}\times{\color{Magenta} 2}+{\color{Blue} 2}\times {\color{Magenta} 1} & {\color{Blue} 1}\times{\color{DarkGreen} 0}+{\color{Blue} 2}\times {\color{DarkGreen} -3}\\
{\color{Red} 0}\times{\color{Magenta} 2}+{\color{Red} 4}\times {\color{Magenta} 1} & {\color{Red} 0}\times {\color{DarkGreen} 0}+{\color{Red} 4}\times {\color{DarkGreen} -3}\\
3\times{\color{Magenta} 2}+-1\times {\color{Magenta} 1} & 3\times {\color{DarkGreen} 0}+-1\times {\color{DarkGreen} -3}
\end{pmatrix}|
2. On effectue la somme de ces produits pour obtenir une nouvelle matrice.
|\begin{pmatrix}
{\color{Blue} 1}\times{\color{Magenta} 2}+{\color{Blue} 2}\times {\color{Magenta} 1} & {\color{Blue} 1}\times{\color{DarkGreen} 0}+{\color{Blue} 2}\times {\color{DarkGreen} -3}\\
{\color{Red} 0}\times{\color{Magenta} 2}+{\color{Red} 4}\times {\color{Magenta} 1} & {\color{Red} 0}\times {\color{DarkGreen} 0}+{\color{Red} 4}\times {\color{DarkGreen} -3}\\
3\times{\color{Magenta} 2}+-1\times {\color{Magenta} 1} & 3\times {\color{DarkGreen} 0}+-1\times {\color{DarkGreen} -3}
\end{pmatrix}=\begin{pmatrix}
4 & -6\\
4 & -12\\
5 & 3
\end{pmatrix}|
Réponse: La nouvelle matrice obtenue est donc |C=\begin{pmatrix}
4 & -6\\
4 & -12\\
5 & 3
\end{pmatrix}|.
La multiplication de deux matrices |A| et |B| n'est pas commutative. En effet, |AB \neq BA| sauf dans des cas très particuliers.