Matières
Niveaux
L'énergie mécanique est une quantité utilisée en physique pour désigner l'énergie d'un système emmagasinée sous forme d'énergie cinétique et d'énergie potentielle.
L'énergie mécanique représente la somme de toutes les énergies existant dans un système. Dans un cas où le système ne rencontre aucune force de frottement, la loi de la conservation de l'énergie s'applique: l'énergie ne sera ni créée ni détruite. Toutefois, elle pourrait être transférée d'un objet à un autre ou transformée en d'autres types d'énergie.
L'image suivante démontre le mouvement d'une planchiste qui se déplace dans une rampe en demi-lune.
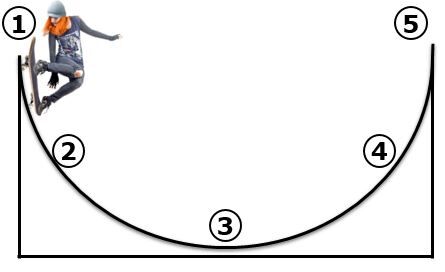
La quantité d'énergie mécanique restera toujours la même, car l'énergie est conservée (assumant qu'il n'y a aucun frottement). Toutefois, le type d'énergie que possède la planchiste va varier selon la position et la vitesse de la planchiste.
En analysant chacun des points, il est possible de comparer les types d'énergie de la planchiste dans son mouvement.
Au point 1, la planchiste est au point le plus haut de la demi-lune. Elle possède donc une énergie potentielle maximale. Toutefois, puisqu'elle amorce son mouvement, elle n'a pas encore d'énergie cinétique.
Au point 2, elle est située au milieu de sa descente dans la demi-lune. Elle a donc converti une partie de son énergie potentielle en énergie cinétique. Toutefois, l'énergie mécanique reste toujours la même.
Au point 3, l'énergie potentielle est nulle, car la planchiste est située à une hauteur nulle (au sol). Cependant, son énergie cinétique est maximale, car elle atteint sa vitesse la plus élevée.
Au point 4, la planchiste perd de la vitesse, mais gagne en hauteur. Elle a donc converti une partie de l'énergie cinétique qu'elle avait au point 3 en énergie potentielle. Néanmoins, l'énergie mécanique reste constante.
Au point 5, la planchiste atteint une hauteur similaire à celle qu'elle avait au point 1. Elle possède donc la même quantité d'énergie potentielle qu'au départ. Puisqu'elle possède la même quantité d'énergie mécanique, l'énergie cinétique sera nulle: elle s'arrêtera à ce moment.
L'énergie mécanique est déterminée à partir de l'équation suivante:
|E_{m} = E_{p} + E_{k}|
où
|E_{m}| représente l'énergie mécanique |\small \text {(J)}|
|E_{p}| représente l'énergie potentielle |\small \text {(J)}|
|E_{k}| représente l'énergie cinétique |\small \text {(J)}|
Quelle vitesse minimale un saumon doit-il avoir pour remonter une chute de |\small \text {2,2 m}| ?

La loi de la conservation de l'énergie permet de déduire que l'énergie mécanique au départ sera la même que celle à la fin du mouvement du saumon.
||\begin{align} E_{m_{i}} &= E_{m_{f}} \\
E_{p_{i}} + E_{k_{i}} &= E_{p_{f}} + E_{k_{f}} \end{align}||
À la fin du mouvement, le saumon s'arrêtera au sommet de la chute. Sa vitesse sera nulle (tout comme son énergie cinétique), alors que l'énergie du saumon sera uniquement sous forme potentielle. Cette énergie provient de la vitesse que le saumon avait au départ, lorsqu'il était en bas de la chute.
Il est donc possible de simplifier la formule ci-dessus afin d'éliminer des termes nuls.
||\begin{align} 0 + E_{k_{i}} &= E_{p_{f}} + 0 \\
E_{k_{i}} &= E_{p_{f}} \\
\displaystyle \frac {1}{2} \times m \times v^{2} &= m \times g \times \triangle y
\end{align}||
Puisque la masse est présente de part et d'autre de l'égalité, cette variable peut être simplifiée. Puisque la question demande quelle est la vitesse du saumon, il suffit d'isoler la variable pour trouver cette vitesse.
||\begin{align}
\displaystyle \frac {1}{2} \times v^{2} = g \times \triangle y \quad \Rightarrow \quad v &= \sqrt {2 \times g \times \triangle y} \\ &= \sqrt {2 \times \text {9,8 m/s}^2 \times \text {2,2 m}} \\ &= \text {6,57 m/s}
\end{align}||
Le saumon a une vitesse initiale de |\text {6,57 m/s}|.
Un cycliste ayant une masse de |\small \text {63 kg}| descend une colline de |\small \text {8 m}| de hauteur après avoir pris une pause. Il arrive au pied de cette colline avec une vitesse de |\small \text {12 m/s}|. Quelle quantité d'énergie a été perdue en raison du frottement ?

Dans une situation comme celle décrite ci-dessus, la conservation de l'énergie est toujours vraie: toutefois, la différence entre l'énergie initiale et l'énergie finale aura été transformée en une autre sorte d'énergie que celles présentes dans la formule de l'énergie mécanique.
Tout d'abord, en calculant l'énergie initiale, le cycliste possède de l'énergie potentielle, car il est situé au haut de la colline. Il ne possède pas d'énergie cinétique, puisqu'il vient de prendre sa pause.
||\begin{align}
E_{m_{i}} = E_{p_{i}} + E_{k_{i}} \quad \Rightarrow \quad E_{m_{i}} &= m \times g \times \triangle y + 0 \\
&= \text {63 kg} \times \text {9,8 N/kg} \times \text {8 m} \\ &= \text {4 939,2 J}
\end{align}||
Au bas de la colline, le cycliste ne possède plus d'énergie potentielle. Il a toutefois une quantité importante d'énergie cinétique accumulée, car sa vitesse est élevée au bas de la colline.
||\begin{align}
E_{m_{f}} = E_{p_{f}} + E_{k_{f}} \quad \Rightarrow \quad E_{m_{f}} &= 0 + \displaystyle \frac {1}{2} \times m \times v^{2} \\
&= \displaystyle \frac {1}{2} \times \text {63 kg} \times \text {(12 m/s)}^{2} \\
&= \text {4 536 J}
\end{align}||
L'énergie mécanique initiale et l'énergie mécanique finale ne sont pas égales. Ceci signifie que la différence d'énergie a été perdue par le frottement.
||\begin{align}
E = E_{m_{i}} - E_{m_{f}} \quad \Rightarrow \quad
E&= \text {4 939,2 J} - \text {4 536 J} \\
&= \text {403,2 J} \\
\end{align}||
Le cycliste a donc perdu |\text {403,2 J}| d'énergie en raison du frottement.
Pour valider ta compréhension à propos de la conservation de l'énergie mécanique de façon interactive, consulte la MiniRécup suivante :
