Matières
Niveaux
La résistance équivalente, ou résistance totale, est la valeur de la résistance qui permettrait de remplacer toutes les résistances d'un circuit par une seule résistance.
Pour déterminer la résistance équivalente d'un circuit électrique, il faut utiliser les lois de Kirchhoff ainsi que la loi d'Ohm pour déterminer la valeur de la résistance équivalente.
Dans un circuit en série, les valeurs de tension s'additionnent pour donner la tension totale:
||U_{tot} = U_{1} + U_{2} + U_{3} + ...||En utilisant la loi d'Ohm, il est possible de substituer la tension |(U)| par |RI|.
||R_{tot}I_{tot}= R_{1}I_{1} + R_{2}I_{2} + R_{3}I_{3} + ...||Dans un circuit en série, l'intensité est toujours la même. En éliminant l'intensité dans chacun des termes, on obtient la formule qui permet de calculer la résistance équivalente dans un circuit en série.
La formule à utiliser pour calculer la résistance équivalente dans un circuit électrique est:
|R_{eq} = R_{1} + R_{2} + R_{3} + ...|
La résistance équivalente dans un circuit en série est donc équivalente à la somme des résistances présentes dans le circuit.
Quelle est la résistance équivalente dans le circuit suivant?
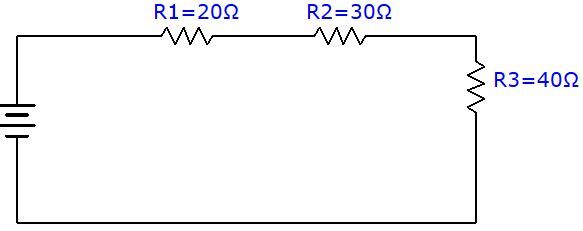
Pour déterminer la résistance équivalente, il suffit d'utiliser la formule et de remplacer les variables par les valeurs connues.
||\begin{align} R_{eq}= R_{1} + R_{2} + R_{3} \quad \Rightarrow \quad R_{eq}&= 20 \:\Omega+30\:\Omega+40\:\Omega \\&= 90 \:\Omega \end{align}||
Quelle est la valeur, en Ohms, de la troisième résistance dans le circuit suivant?
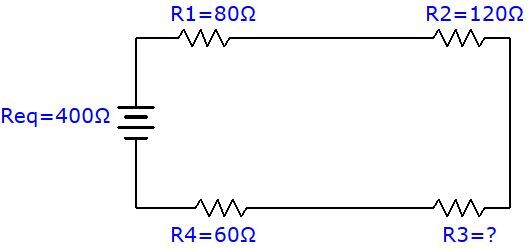
Pour déterminer la résistance manquante, il faut utiliser la formule de la résistance équivalente et isoler la variable manquante pour trouver la réponse.
||\begin{align} R_{eq}= R_{1} + R_{2} + R_{3} + R_{4} \quad \Rightarrow \quad R_{3} &= R_{eq} - R_{1} - R_{2} - R_{4} \\ &= 400 \: \Omega - 80 \: \Omega - 120 \: \Omega - 60 \:\Omega \\ &= 140 \:\Omega \end{align}||
Dans un circuit en parallèle, les valeurs d'intensité s'additionnent pour donner l'intensité totale dans le circuit électrique:
||I_{tot} = I_{1} + I_{2} + I_{3} + ...|| En utilisant la loi d'Ohm, il est possible de substituer l'intensité |(I)| par |\displaystyle \frac {U}{R}|.
||\displaystyle \frac {U_{tot}}{R_{tot}}= \frac {U_{1}}{R_{1}} + \frac {U_{2}}{R_{2}} + \frac {U_{3}}{R_{3}} + ...||Dans un circuit en parallèle, la tension est toujours la même. En éliminant la tension dans chacun des termes, on obtient la formule qui permet de calculer la résistance équivalente dans un circuit en parallèle.
La formule à utiliser pour calculer la résistance équivalente dans un circuit électrique est:
|\displaystyle \frac {1}{R_{eq}} = \frac {1}{R_{1}} + \frac {1}{R_{2}} + \frac {1}{R_{3}} + ...|
À partir de cette formule, il est possible de déduire que la résistance équivalente d'un circuit diminuera chaque fois qu'un résistor sera ajouté dans un circuit en parallèle.
La valeur de la résistance équivalente dans un circuit en parallèle sera toujours plus petite que la valeur de la plus petite résistance du circuit électrique.
Quelle est la valeur de la résistance équivalente dans le circuit en parallèle suivant?
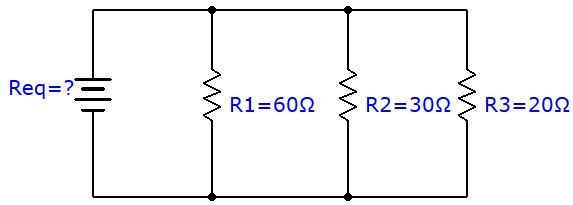
Pour déterminer la résistance équivalente, il suffit d'utiliser la formule et de remplacer les variables par les valeurs connues.
\begin{align} \frac{1}{R_{eq}}= \frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}} \quad \Rightarrow \quad \frac{1}{R_{eq}} &= \frac{1}{60 \: \Omega}+\frac{1}{30 \: \Omega}+\frac{1}{20 \: \Omega} \\ \frac{1}{R_{eq}} &= \frac{6}{60 \: \Omega} \\ R_{eq} &= 10 \:\Omega \end{align} Comme il a été mentionné auparavant, la résistance équivalente est plus petite que la plus petite des résistances dans ce circuit |(10 \space \Omega < 20 \space \Omega)|.
Quelle doit être la valeur de la résistance |R_{1}| pour que la résistance de ce circuit en parallèle soit égale à |\small 150 \space \Omega|?
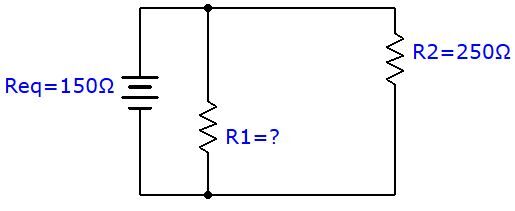
Pour déterminer la résistance manquante, il faut utiliser la formule de la résistance équivalente et isoler la variable manquante pour trouver la réponse.
||\begin{align} \frac{1}{R_{eq}}= \frac{1}{R_{1}}+\frac{1}{R_{2}} \quad \Rightarrow \quad \frac{1}{R_{1}} &= \frac{1}{R_{eq}}-\frac{1}{R_{2}} \\\frac{1}{R_{1}} &= \frac{1}{150 \: \Omega}-\frac{1}{250 \: \Omega} \\ \frac{1}{R_{1}}&= \frac{4}{1\:500 \: \Omega} \\ R_{1} &= 375 \:\Omega \end{align} ||
Pour valider ta compréhension à propos des calculs dans les circuits électriques de façon interactive, consulte la MiniRécup suivante :
