Matières
Niveaux
L’ensemble des nombres entiers, représenté par le symbole |\mathbb{Z},| regroupe tous les nombres naturels (entiers positifs) et leurs opposés (entiers négatifs).||\mathbb{Z} = \{\ldots,-3,-2,-1,0,1,2,3,\ldots\}||On utilise aussi l’appellation nombres entiers relatifs.
Tout comme les nombres naturels, les nombres entiers ont une partie décimale nulle.
Des nombres sont opposés s’ils sont de signes contraires et à une même distance de |0.|
Des nombres opposés sont des nombres qui ont la même valeur absolue, mais l’un est positif alors que l’autre est négatif.
De plus, on dit que 2 nombres sont opposés lorsque leur somme est nulle.
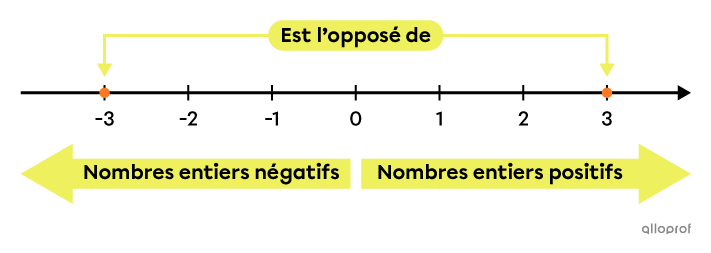
Le nombre |-3| est l’opposé du nombre |3.| Ces 2 nombres sont à la même distance de |0,| mais ils sont de signes contraires.
De plus, la somme de ces 2 nombres est nulle, car |-3+3=0.|
Contrairement aux nombres négatifs qui sont toujours précédés du signe « – », les nombres positifs sont généralement écrits sans le signe « + ».
La notion d’opposé d’un nombre n’est pas uniquement applicable dans |\mathbb{Z},| mais dans la majorité des sous-ensembles des nombres réels |(\mathbb{R}).|
Sur une droite numérique, les nombres entiers peuvent être représentés par des points à la position des entiers positifs et négatifs.
Les points orange sur la droite numérique ci-dessous représentent quelques éléments de l’ensemble des nombres entiers.

Les nombres entiers |(\mathbb{Z})| forment un sous-ensemble des nombres réels |(\mathbb{R})| et ils incluent l’ensemble des nombres naturels |(\mathbb{N}).| On peut utiliser cette notation pour le représenter.||\mathbb{N}\subset\mathbb{Z}||Cela se lit : « l’ensemble des nombres naturels est inclus dans l’ensemble des nombres entiers ».
Voici un schéma qui démontre l’emplacement des nombres naturels |(\mathbb N)| dans l’ensemble des nombres entiers |(\mathbb Z).|

Le nombre |8,| le nombre |-92\ 683,| le nombre |-11| ainsi que leurs opposés font partie des nombres entiers.
Les nombres représentés par |-\dfrac{8}{4}| et |\dfrac{54}{9}| font partie de l’ensemble des nombres entiers, car ils correspondent respectivement aux nombres |-2| et |6.| Les opposés de ces nombres appartiennent aussi aux nombres entiers.
Les nombres |1\ 521{,}46| et |-95{,}431| ne font pas partie des nombres entiers, car ils possèdent une partie décimale non nulle. Il en va de même pour la fraction |\dfrac{20}{3}.|
En utilisant la notation appropriée, on obtient |-92\ 683\in\mathbb{Z}| et |1\ 521{,}46\notin\mathbb{Z}.|
On note |\mathbb {Z}^*| l’ensemble des nombres entiers dont on a enlevé le nombre |0.|||\mathbb {Z}^* = \{...,-3, -2, -1, 1, 2, 3, ... \}||
On note |\mathbb {Z}_+| l’ensemble des nombres entiers positifs. Dans ce cas, c’est le même ensemble que l’ensemble des nombres naturels |(\mathbb N).|||\mathbb {Z}_+ = \{ 0, 1, 2, 3, ... \} = \mathbb N||
On note |\mathbb {Z}_-| l’ensemble des nombres entiers négatifs.||\mathbb {Z}_- = \{ ... ,-5, -4, -3, -2, -1, 0 \}||
Il est possible de combiner ces notations. Par exemple, on note |\mathbb {Z}_-^*| l’ensemble des nombres entiers négatifs sans le nombre |0.|
Les étages dans un ascenseur sont représentés à l’aide de nombres entiers. Au niveau du sol, on est à l’étage 0. Si on monte au-dessus du niveau du sol avec l’ascenseur, on se retrouve aux niveaux 1, 2, 3, etc. Si on choisit plutôt de descendre et d’aller sous le niveau du sol, on se retrouve aux étages -1, -2, -3, etc.
Un nombre négatif est un nombre qui est inférieur ou égal à |0.|
Plusieurs situations de la vie courante impliquent des nombres négatifs.
On mesure la température à l’aide d’un thermomètre gradué en degré Celsius |(^\circ\text{C}).| En été, la température est supérieure à |0\ ^\circ\text{C};| elle est donc représentée par des nombres positifs. Toutefois, en hiver, la température tombe sous le point de congélation de l’eau et devient inférieure à |0\ ^\circ\text{C}.| Ainsi, on utilise les nombres négatifs pour décrire les température inférieures à |0\ ^\circ\text{C}.|

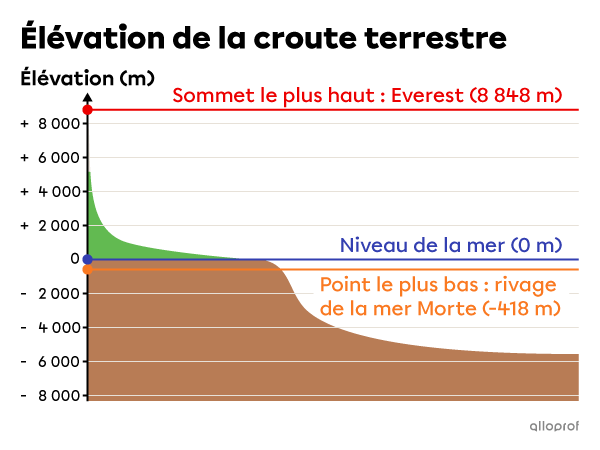
L’altitude est la distance verticale mesurée entre un point du relief terrestre et le niveau de la mer. On exprime cette hauteur ou cette profondeur à l’aide d’une échelle graduée en mètres. Le |0| de l’échelle représente le niveau de la mer.