Matières
Niveaux
L’algèbre est la branche des mathématiques qui généralise les règles de calculs arithmétiques à l’aide de variables.
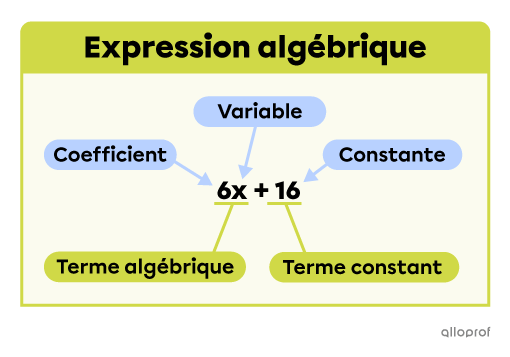
Une expression algébrique est un ensemble de termes algébriques et constants reliés entre eux par des additions |(+)| et des soustractions |(-).|
Un terme est un élément d’une expression algébrique qui est composé d’un nombre et/ou de variables.
Une variable est une lettre qui peut prendre différentes valeurs.
Un coefficient est un nombre qui multiplie une ou plusieurs variables.
Une constante est un nombre qui ne multiplie pas une variable.

Un terme peut prendre plusieurs formes.
| Pas de coefficient visible | Présence d’un coefficient | |
|---|---|---|
| Aucune variable |
|25| |
|
| 1 variable |
|x| |
|5x| |
| Plusieurs variables |
|xy| |
|5xy| |
| 1 ou des variables affectées d’exposants |
|x^2y| |
|5x^2y| |
En algèbre, il existe des conventions d’écriture.
La façon d’exprimer une multiplication entre différents éléments est de coller ces éléments. Ainsi, |6c| signifie |6\times c| et |7a^2b| signifie |7\times a\times a \times b.|
Dans le même ordre d’idée, lorsqu’un terme n’affiche pas de coefficient, on considère que son coefficient vaut 1. En effet, |1b = 1\times b = b| puisque le nombre |1| est l’élément neutre de la multiplication.
Il en est de même pour les exposants. Lorsqu’une variable n’affiche pas d’exposant, on considère que l’exposant vaut 1. En effet, |5x=5x^1| et |10xy^2=10x^1y^2.|
Par ailleurs, les expressions algébriques peuvent être composées d’un seul terme ou de plusieurs termes.
S’il n’y a qu’un seul terme, l’expression algébrique est un monôme.
Exemples : |x,| |8y,| |-4ab,| |\dfrac{9a^2b}{5},| |5a\times 3b,| |8a \div 3|
S’il y a plusieurs termes, l’expression algébrique est un polynôme.
Exemples : |x-y,| |x^3+x^2+x+1,| |25x^2y^4-16,| |15ab + 3c \times 6,| |\dfrac{5a+3b}{2}|
On pourrait croire que l’expression algébrique |15ab + 3c \times 6| est composée de 3 termes, mais elle n’en contient que 2. En effet, les termes doivent être séparés par des symboles |+| et |-.| Autrement dit, |3c \times 6| ne compte que pour un seul terme.
De même, l’expression |8a \div 3| est bel et bien un monôme. Il est préférable de réécrire cette expression en utilisant la notation fractionnaire de la façon suivante. ||8a\div 3=\dfrac{8a}{3} =\dfrac{8}{3}a||Ainsi, le coefficient du monôme est |\dfrac{8}{3}.|
Une expression algébrique sert à généraliser des calculs, car elle correspond à une chaine d’opérations où certaines quantités ont été remplacées par des lettres qu’on nomme variables.
Ainsi, à partir d’une 1re quantité qui peut prendre différentes valeurs, on peut, à partir d’un énoncé, déterminer une expression algébrique représentant une autre quantité qui dépend de la 1re. C’est ce qu’on appelle traduire un énoncé en expression algébrique.
À partir de l’énoncé « ton frère a |2| ans de plus que toi », on peut construire la table de valeurs suivante.
| Ton âge (ans) |
L'âge de ton frère (ans) |
|---|---|
| |3| | |3+2=5| |
| |8| | |8+2=10| |
| |12| | |12+2=14| |
| ... | ... |
On remarque alors que le calcul qui donne l’âge de ton frère est toujours de la forme suivante.||\text{Ton âge}+2=\text{L’âge de ton frère}||Ainsi, si tu remplaces « Ton âge » par la variable |a,| l’expression algébrique qui représente l’âge de ton frère devient |a+2.| ||a+2=\text{L’âge de ton frère}||Il s’agit d’une expression composée de 2 termes : |a| et |2.| Le 1er terme est composé uniquement de la variable |a| et le 2e terme est un terme constant, car ton frère a toujours |2| ans de plus que toi, même si ton âge varie avec les années.
Lorsqu’une expression algébrique est égale à un terme constant ou à une autre expression algébrique, on obtient ce qu’on appelle une équation.
Variable : |x|
Terme constant : |23|
Expressions algébriques : |4x-5| et |2x+7|
Équations qui expriment l’égalité entre une expression algébrique et un terme constant : |4x-5=23| et |23=2x+7|
Équation qui exprime l’égalité entre 2 expressions algébriques : |4x-5=2x+7|
Dans une expression algébrique, des termes sont semblables lorsqu’ils sont composés des mêmes variables affectées des mêmes exposants.
Les termes |4x| et |5x| sont semblables, car ils ont la même variable |(x)| affectée du même exposant, soit |1.|
Les termes |3r^2s^3| et |6r^2s^3| sont semblables, car on retrouve les mêmes variables |(r| et |s)| affectées des mêmes exposants |(2| pour la variable |r| et |3| pour la variable |s).|
Les termes |\dfrac{8}{3}ab| et |\dfrac{7ba}{4}| sont semblables même si les variables ne sont pas dans le même ordre. En effet, selon la commutativité de la multiplication, |a\times b = b\times a.| Par contre, pour respecter les conventions d’écriture en algèbre, il faudrait écrire le 2e terme comme ceci : |\dfrac{7}{4}ab.|
Les termes |3xy| et |3xyz| ne sont pas semblables, car ils n’ont pas les mêmes variables.
Les termes |12r^2 s^3 t| et |2r^2 s^3 t^2| ne sont pas semblables car la variable |t| n’est pas affectée du même exposant dans les 2 termes.
Les termes |2a^2b^3c^4| et |3b^2 c^3 a^4| ne sont pas semblables. Il est vrai qu’on y retrouve les 3 mêmes variables : |a,| |b| et |c,| et les 3 mêmes exposants : |2,| |3| et |4.| Cependant, on ne trouve pas la même correspondance entre les variables et les exposants.
Comme son nom l’indique, la valeur d’une variable peut varier selon la situation et c’est cette caractéristique qu’il faut exploiter. On donne la valeur voulue à une variable selon le contexte dans lequel on l’utilise.
Le remplacement d’une variable par un nombre s’appelle une substitution.
Ainsi, après avoir substitué les variables par des nombres, une expression algébrique devient une chaine d’opérations. Il ne reste plus qu’à effectuer le calcul en respectant la priorité des opérations.
Si |x = 2| dans l’expression algébrique |2x +3,| on remplace la variable par sa valeur.||\begin{align} 2\boldsymbol{\color{#3b87cd}x}+3 &=2(\boldsymbol{\color{#3b87cd}2})+3 \\ &= 4+3\\ &= 7 \end{align}||Ainsi, dans le cas où |x=2,| la valeur de l’expression algébrique est de |7.|
Si |a=-1{,}5| et que |b=10| dans l’expression algébrique |3a-\dfrac{b}{5}+2,| il faut effectuer 2 substitutions.||\begin{align}3\boldsymbol{\color{#3b87cd}a}-\dfrac{\boldsymbol{\color{#3a9a38}b}}{5}+2 &=3(\boldsymbol{\color{#3b87cd}{-1{,}5}})-\dfrac{\boldsymbol{\color{#3a9a38}{10}}}{5}+2\\[3pt] &= -4{,}5-2+2\\[3pt] &=-4{,}5\end{align}||Ainsi, dans ce cas, l’expression algébrique vaut |-4{,}5.|
Si |w=5| dans l’expression |-w^2+w+20,| il faut remplacer |w| par |5| à tous les endroits où |w| apparait.||\begin{align}-\boldsymbol{\color{#3b87cd}w}^2 + \boldsymbol{\color{#3b87cd}w}+20 &=-\boldsymbol{\color{#3b87cd}{5}}^2 + \boldsymbol{\color{#3b87cd}{5}}+20\\ &= -25+5+20\\ &=0\end{align}||
Lorsqu'on écrit une expression algébrique, il importe de respecter certaines conventions d'écriture.

Dans un terme, le coefficient est toujours écrit devant les variables. Il est important de noter qu'un coefficient de |1| n'est toutefois pas écrit dans une expression.
Si un terme comporte plusieurs variables, il est convenu de placer ces variables en respectant l’ordre alphabétique.
Dans un polynôme, les termes sont disposés dans l’ordre décroissant de leur degré respectif. Si 2 termes sont du même degré, on les écrit alors selon l’ordre alphabétique.
| Convention | Convention non respectée | Convention respectée |
|---|---|---|
|
|b15c^2| ne respecte pas la convention puisqu’il ne débute pas par son coefficient. |
Il faut plutôt écrire |
|
|3zx^2y| ne respecte pas la convention puisque les variables n’y sont pas inscrites en ordre alphabétique. |
Il faut plutôt écrire |
|
|6+5x^2+4y^3| ne respecte pas la convention puisque ses termes ne sont pas en ordre décroissant de degré. |
Il faut plutôt écrire |
|
|4b-5a| ne respecte pas la convention puisque les termes du même degré ne sont pas en ordre alphabétique. |
Il faut plutôt écrire |