Matières
Niveaux
Pour calculer le périmètre d’un polygone régulier, on a besoin de connaitre la mesure du côté et le nombre de côtés. Pour calculer l’aire, on doit aussi connaitre la mesure de l’apothème.
Comme pour le périmètre d’une figure plane, on calcule le périmètre d’un polygone régulier en additionnant la mesure de tous ses côtés. Or, puisque les côtés d’un polygone régulier ont tous la même mesure, on peut généraliser le calcul de son périmètre de la façon suivante.
||\begin{align}P&=\overbrace{c+c+\ldots+c}^{\large\text{$n$ fois}}\\&=n\times c\end{align}||
où
|P:| Périmètre du polygone régulier
|n:| nombre de côtés
|c:| mesure d’un côté
En déplaçant le curseur dans l’animation interactive suivante, on peut observer comment il est possible de calculer le périmètre d’un polygone régulier.
Quel est le périmètre d’un ennéagone régulier dont la mesure d’un côté est |5{,}2\ \text{cm}|?
Un ennéagone est un polygone à |9| côtés. On calcule donc le périmètre de cet ennéagone régulier de la façon suivante.||\begin{align}P&=n\times c\\&=9\times5{,}2\\&=46{,}8\ \text{cm}\end{align}||Réponse : Le périmètre de l’ennéagone régulier est de |46{,}8\ \text{cm}.|
Il faut parfois utiliser la relation de Pythagore pour arriver à calculer le périmètre d’un polygone régulier.
Quel est le périmètre de cet heptagone régulier?
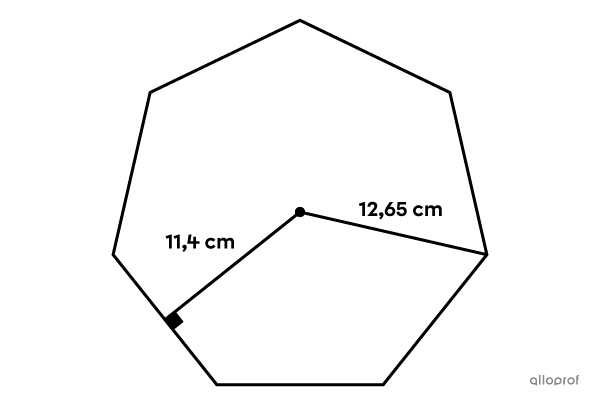
Il est possible de dégager certaines conjectures en comparant le périmètre de polygones réguliers équivalents.
Le calcul de l’aire d’un polygone régulier est souvent présenté à l’aide de l’une des 2 formules suivantes.
||A=\dfrac{c\times a\times n}{2}||
||A=\dfrac{P\times a}{2}||
où
|A:| aire du polygone régulier
|c:| mesure d’un côté
|a:| apothème
|n:| nombre de côtés
|P:| périmètre
Ces 2 équations sont équivalentes. En effet, pour passer de l’une à l’autre, il suffit d’utiliser la formule du périmètre d’un polygone régulier.||\begin{align}A&=\dfrac{c\times a\times n}{2}\\[3pt]&=\dfrac{\boldsymbol{n\times c}\times a}{2}\\[3pt]&=\dfrac{\boldsymbol{P}\times a}{2}\\[3pt]\end{align}||
Les 2 formules sont issues d’une démonstration géométrique différente. En effet, on peut expliquer le calcul de l’aire d’un polygone régulier à l’aide de l’une des 2 méthodes suivantes.
En déplaçant le curseur dans l’animation interactive suivante, on peut observer comment il est possible de calculer l’aire d’un polygone régulier à l’aide de la méthode de la somme de l’aire des triangles.
Un polygone régulier à |n| côtés peut être décomposé en |\boldsymbol{n}| triangles isocèles isométriques. Autrement dit, pour calculer l’aire d’un polygone régulier, il suffit de multiplier l’aire d’un des triangles par le nombre de triangles.||\begin{alignat}{13}A_\text{polygone régulier}&=\qquad\!A_\text{triangle}&&\times\begin{gathered}\text{Nombre de}\\\text{triangles}\end{gathered}\\[3pt]&=\;\dfrac{\color{#3b87cd}{\textbf{Base}}\times\color{#fa7921}{\textbf{Hauteur}}}{2}&&\times\begin{gathered}\text{Nombre de}\\\text{triangles}\end{gathered}\end{alignat}||Or, on a les équivalences suivantes.
La base du triangle correspond à la mesure d’un côté du polygone régulier |(\boldsymbol{\color{#3b87cd}{c}}).|
La hauteur du triangle correspond à l’apothème du polygone régulier |(\boldsymbol{\color{#fa7921}{a}}).|
Le nombre de triangles correspond au nombre de côtés du polygone régulier |(\boldsymbol{n}).|
Ainsi, en remplaçant les termes de l’équation précédente par les variables correspondantes, on obtient la formule suivante.||\begin{align}A&=\dfrac{c\times a}{2}\times n\\[3pt]&=\dfrac{c\times a\times n}{2}\end{align}||
Quelle est l’aire de ce polygone régulier?
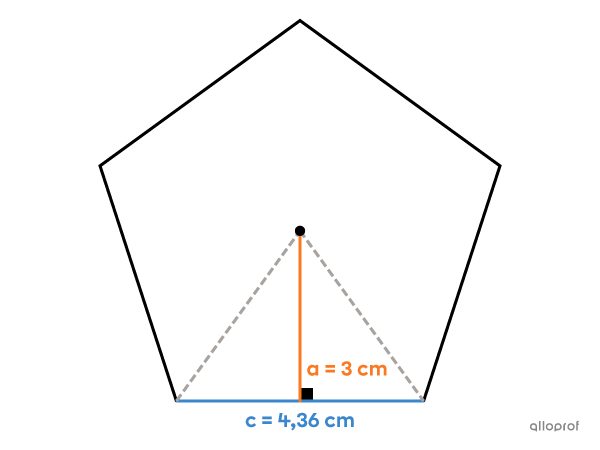
Il s’agit d’un pentagone régulier, c’est-à-dire d’un polygone à |5| côtés |(n=5).| On connait la mesure d’un côté |(c=4{,}36\ \text{cm})| et la mesure de l’apothème |(a=3\ \text{cm}).| On calcule donc l’aire de ce pentagone régulier de la façon suivante.||\begin{align}A&=\dfrac{\boldsymbol{\color{#3b87cd}{c}}\times\boldsymbol{\color{#fa7921}{a}}\times\boldsymbol{n}}{2}\\[3pt]&=\dfrac{\boldsymbol{\color{#3b87cd}{4{,}36}}\times\boldsymbol{\color{#fa7921}{3}}\times\boldsymbol{5}}{2}\\[3pt]&=32{,}7\ \text{cm}^2\end{align}||Réponse : L’aire de ce pentagone régulier est de |32{,}7\ \text{cm}^2.|
En déplaçant le curseur dans l’animation interactive suivante, on peut observer comment il est possible de calculer l’aire d’un polygone régulier à l’aide de la méthode de l’aire d’un parallélogramme.
Un polygone régulier peut être décomposé en triangles, puis doublé, afin de former un parallélogramme. Autrement dit, pour calculer l’aire d’un polygone régulier, il suffit de diviser l’aire du parallélogramme par |2.|||\begin{alignat}{13}A_\text{polygone régulier}&=\dfrac{A_\text{parallélogramme}}{2}\\[3pt]&=\;\dfrac{\text{Base}\times\text{Hauteur}}{2}\\[3pt]\end{alignat}||Or, dans le polygone régulier, on a les équivalences suivantes.
La base du parallélogramme correspond à la mesure du périmètre |(\boldsymbol{\color{#3b87cd}{P}}).|
La hauteur du parallélogramme correspond à l’apothème |(\boldsymbol{\color{#fa7921}{a}}).|
Ainsi, en remplaçant les termes de l’équation précédente par les variables correspondantes, on obtient la formule suivante.||A=\dfrac{P\times a}{2}||
Quelle est l’aire de ce polygone régulier?
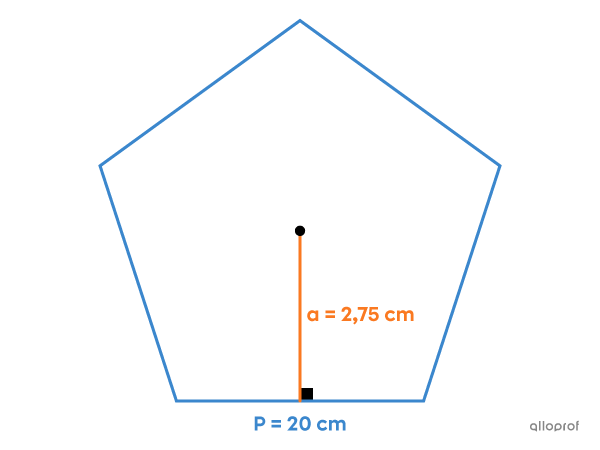
Il s’agit d’un pentagone régulier, c’est-à-dire d’un polygone à |5| côtés. On connait la mesure du périmètre |(P=20\ \text{cm})| et la mesure de l’apothème |(a=2{,}75\ \text{cm}).| On calcule donc l’aire de ce pentagone régulier de la façon suivante.||\begin{align}A&=\dfrac{\boldsymbol{\color{#3b87cd}{P}}\times\boldsymbol{\color{#fa7921}{a}}}{2}\\[3pt]&=\dfrac{\boldsymbol{\color{#3b87cd}{20}}\times\boldsymbol{\color{#fa7921}{2{,}75}}}{2}\\[3pt]&=27{,}5\ \text{cm}^2\end{align}||Réponse : L’aire de ce pentagone régulier est de |27{,}5\ \text{cm}^2.|
Il faut parfois utiliser la relation de Pythagore pour arriver à calculer l’aire d’un polygone régulier.
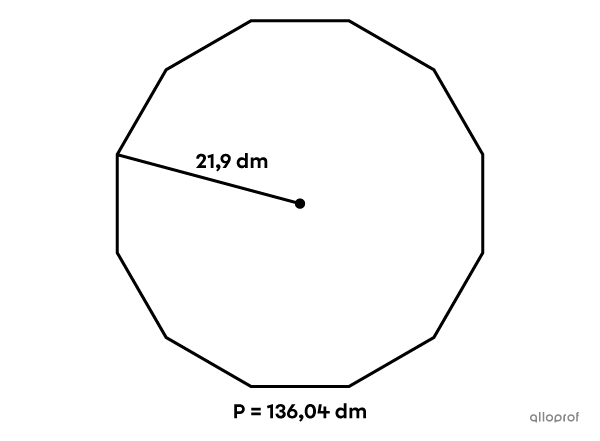
Quelle est l’aire de ce dodécagone régulier?
Pour valider ta compréhension de l'aire et du périmètre des figures planes de façon interactive, consulte la MiniRécup suivante :
