Matières
Niveaux
Pour construire un cercle, on utilise un compas avec une ouverture correspondant au rayon.
Pour bien comprendre le cercle, il faut définir certains termes. De plus, d’autres notions connexes peuvent être consultées.
Un rayon, généralement noté |r,| est un segment qui relie un point quelconque du cercle à son centre.
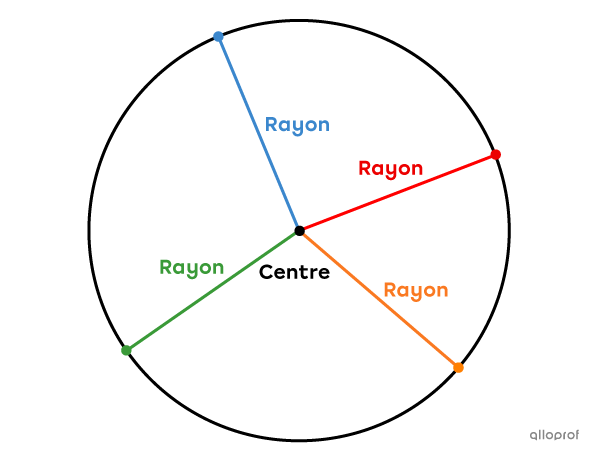
Puisque le cercle est fait d'une infinité de points, il possède une infinité de rayons.
Lorsqu’on prolonge un rayon au-delà du centre pour aller rejoindre un autre point sur le cercle, on obtient un diamètre.
Un diamètre, généralement noté |d,| est un segment qui relie 2 points du cercle tout en passant par le centre.
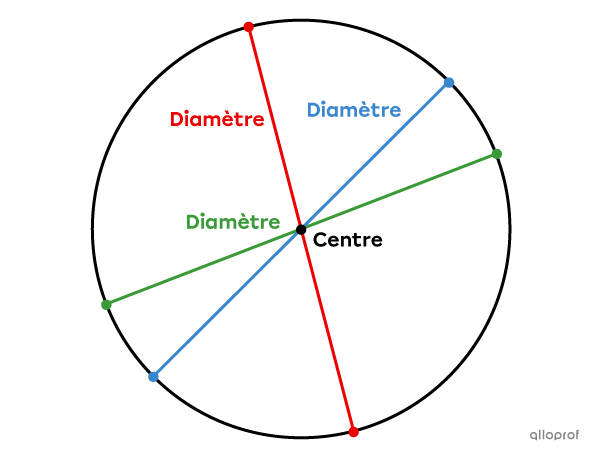
Puisque le cercle possède une infinité de rayons, il a aussi une infinité de diamètres.
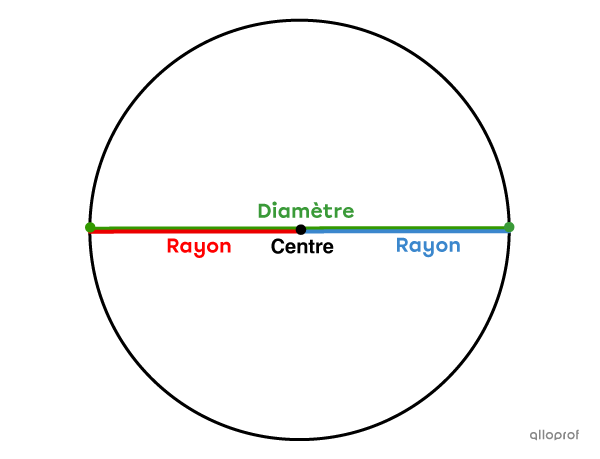
Puisque les rayons et les diamètres passent par le centre du cercle, il est possible d'établir un lien entre leur mesure. En effet, la mesure du diamètre est le double de la mesure du rayon.||d=2r\ \ \text{ou}\ \ r=\dfrac{d}{2}||


Une corde est un segment qui relie 2 points quelconques du cercle sans nécessairement passer par le centre.

On peut donc déduire de cette définition qu'un diamètre est une corde, mais n’est pas un rayon. Le diamètre est d’ailleurs la plus grande corde du cercle.
De plus, puisque le cercle est composé d’une infinité de points, il contient aussi une infinité de cordes.
Un angle au centre est formé par 2 rayons.
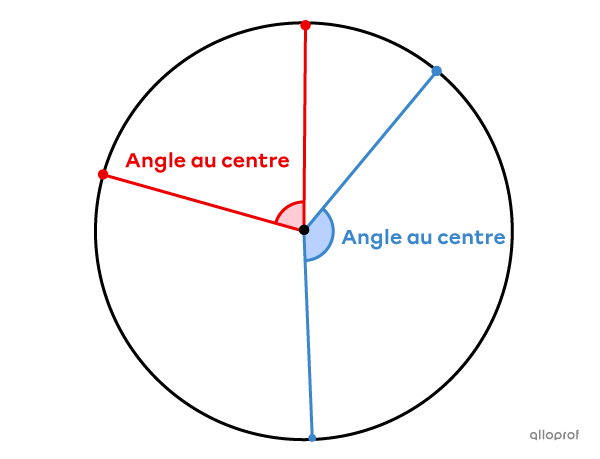
La valeur d’un angle au centre est généralement donnée par une mesure entre |0^\circ| et |360^\circ.| Son sommet est au centre du cercle.
La notion d'angle au centre est liée à celles d'arc de cercle et de secteur circulaire. En effet, l'angle au centre permet de définir une portion du cercle ou du disque.
La circonférence, généralement notée |C,| est le périmètre d'un cercle.
Il est possible de dérouler le cercle pour mesurer sa circonférence.
Remarque : Le terme périmètre désigne le contour de toutes les figures planes, alors que le terme circonférence est réservé aux cercles.
Pour calculer la circonférence d’un cercle, on doit employer une formule qui fait intervenir la mesure de son rayon ou celle de son diamètre.
Un arc de cercle est une portion de la circonférence.
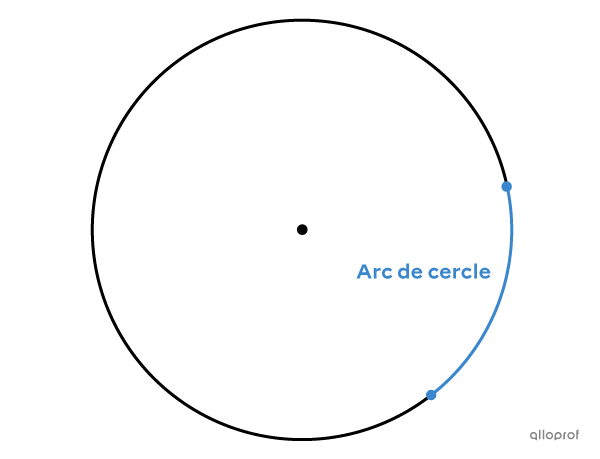
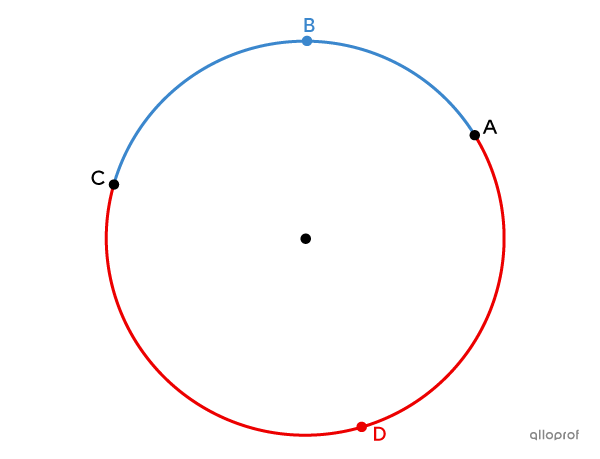
Est-ce que |\overset{\huge\frown}{AC}| désigne l’arc qui passe par le point |B| ou celui qui passe par le point |D|? Pour nommer un arc de cercle, on utilise les points qui le délimitent. Par contre, pour éviter toute confusion, il arrive qu’on ajoute une 3e lettre au nom d’un arc. Dans la figure suivante, on a 2 arcs de cercle : |\color{#3b87cd}{\overset{\Huge\frown}{ABC}}| et |\color{#ec0000}{\overset{\Huge\frown}{ADC}}.|
Pour déterminer la mesure d'un arc de cercle, il faut connaitre la mesure de l’angle au centre qui lui est associé.
Lorsqu'on s’intéresse à la région à l'intérieur d'un cercle, on parle d'un disque et non plus d'un cercle.
Un disque est la région fermée délimitée par un cercle.

Pour calculer l’aire d’un disque, on doit employer une formule qui fait intervenir la mesure de son rayon.
Un secteur circulaire est une région délimitée par un arc de cercle et par 2 rayons.

En d'autres mots, le secteur circulaire représente une fraction de l'aire totale du disque. Pour trouver son aire, il est possible d’établir une proportion avec l’aire totale du disque.
En statistique, on utilise les secteurs pour tracer des diagrammes circulaires.
Un angle inscrit est formé par 2 cordes et son sommet est situé sur le cercle.
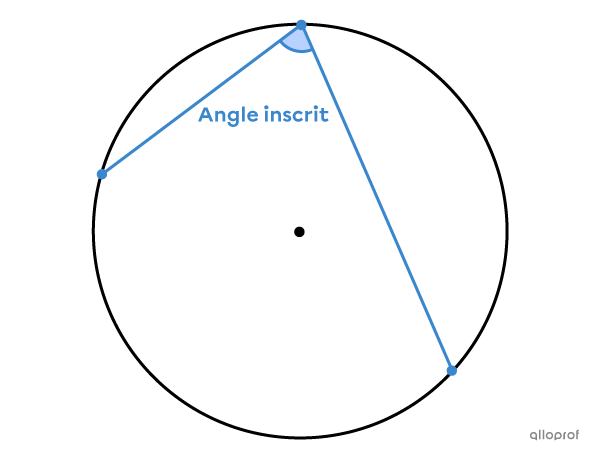
Le sommet de l’angle inscrit est sur le cercle et ses côtés interceptent un arc de cercle.
Pour déterminer la mesure d’un angle inscrit ou celle de l'arc qui est intercepté, on utilise les relations métriques dans le cercle.
Un cercle inscrit est un cercle tangent à tous les côtés d’un polygone.

En d'autres mots, il s'agit du plus grand cercle qui se trouve à l'intérieur d'un polygone. Le cercle doit avoir un point en commun avec chaque côté du polygone. On peut construire un cercle inscrit à l'aide d'une méthode impliquant les bissectrices.
Dans les polygones réguliers, on associe le rayon du cercle à l'apothème du polygone régulier.

Un cercle circonscrit est un cercle qui passe par tous les sommets d'un polygone.

À l'inverse du cercle inscrit, le cercle circonscrit se trouve à l'extérieur du polygone. On peut construire un cercle circonscrit à l'aide d'une méthode impliquant les médiatrices.
Dans les polygones réguliers, les rayons du cercle sont associés aux côtés isométriques des triangles isocèles qui le composent.

Une tangente à un cercle est une droite qui touche le cercle en un seul point. Cette droite est perpendiculaire au rayon du cercle passant par ce même point.
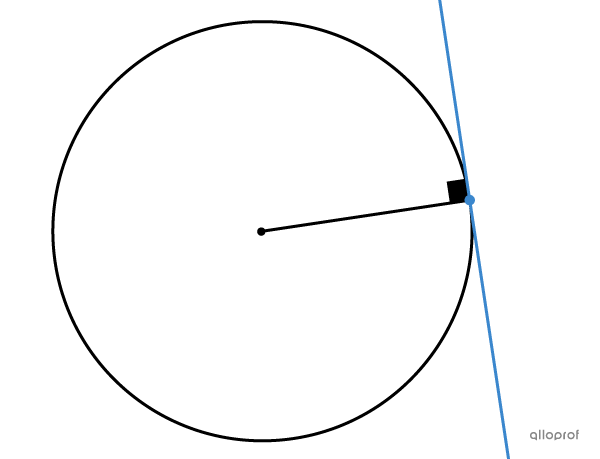
On utilise la géométrie analytique pour arriver à déterminer l’équation d’une tangente à un cercle.
Pour réviser des notions de géométrie, joue à La foire.
