Matières
Niveaux
Dans un cercle, un angle au centre permet de former :
Comme l'angle au centre, l'arc de cercle et le secteur d'un disque sont liés à la même portion d'un cercle, il est possible de déterminer une de ces mesures à partir des proportions suivantes :
||\dfrac{\text{Angle au centre}}{360^\circ}=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}}||
Un arc de cercle représente une partie de la circonférence du cercle et est formé par la rencontre de deux rayons sur la circonférence.
Si on compare le cercle à une roue de bicyclette, l'arc de cercle correspond à une section de la roue comprise entre deux rayons.
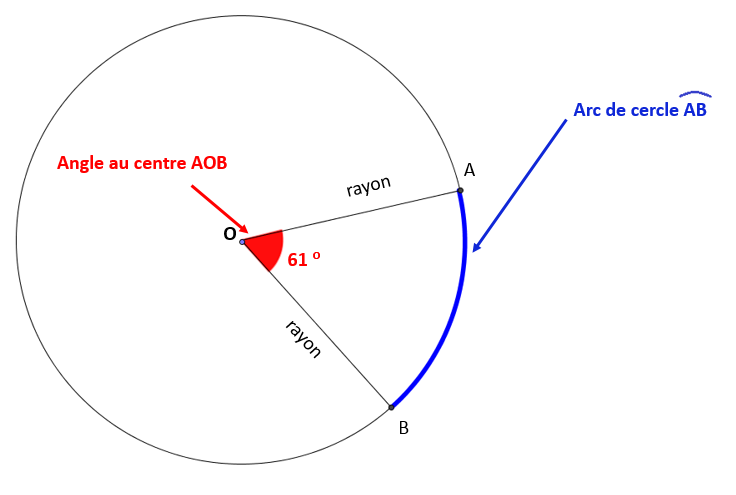
L'arc de cercle représente une portion de la circonférence au même titre que l'angle au centre correspond à une portion d'un tour complet. Puisque ces portions correspondent au même rapport, on peut obtenir la longueur de l'arc de cercle en utilisant une proportion. On l'obtient en effectuant le produit croisé selon le rapport suivant :
||\dfrac{\text{Angle au centre}}{360^\circ}=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}||
Calculer la mesure de l'arc de cercle |\overset{\ \huge\frown}{AB}| inscrit par un angle au centre de |120^\circ| et dont le rayon vaut |3\ \text{cm}.|
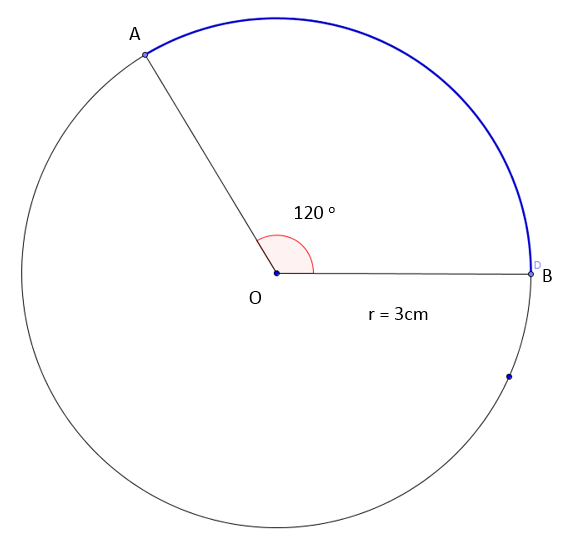
||\begin{align}\dfrac{\text{Angle au centre}}{360^\circ}&=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}\\[3pt] \dfrac{120^\circ}{360^\circ}&=\dfrac{\text{m}\overset{\,\huge\frown}{AB}}{2\pi (3)}\\[3pt] \dfrac{120^\circ}{360^\circ}&=\dfrac{\text{m}\overset{\,\huge\frown}{AB}}{18{,}84\ \text{cm}}\\[5pt] \Rightarrow\ \text{m}\overset{\,\huge\frown}{AB} &= \dfrac{120^\circ\times 18{,}84\ \text{cm}}{360^\circ}= 6{,}28\ \text{cm}\end{align}||Ainsi, |\overset{\,\huge\frown}{AB}| mesure |6{,}28\ \text{cm}.|
Si un arc de cercle |\overset{\huge\frown}{CD}| mesure |15\ \text{cm}| et que la circonférence vaut |120\ \text{cm},| quelle est la mesure de l'angle au centre qui délimite cet arc de cercle?
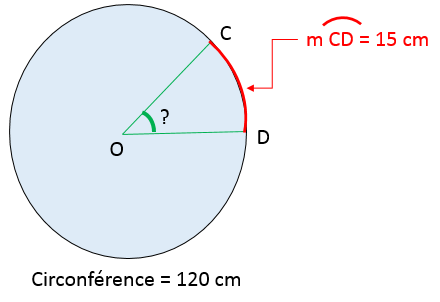
||\begin{align}\dfrac{\text{Angle au centre}}{360^\circ}&=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}\\[5pt] \dfrac{\text{m}\angle DOC}{360^\circ}&=\dfrac{15\ \text{cm}}{120\ \text{cm}}\\[5pt] \Rightarrow\ \text{m}\angle DOC &= \dfrac{15\ \text{cm}\times 360^\circ}{120\ \text{cm}} = 45^\circ \end{align}||Ainsi, l'angle au centre mesure |45^\circ.|
Dans un cercle, le rapport des mesures de 2 angles au centre est égal au rapport des mesures des arcs interceptés par leurs côtés.
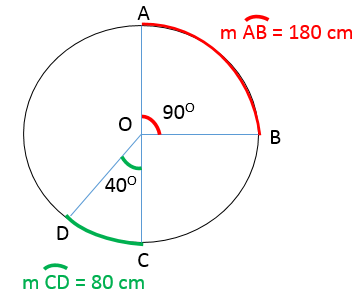
||\begin{align}\dfrac{\text{m}\angle{AOB}}{\text{m}\angle{COD}} &= \dfrac{\text{m}\overset{\,\huge\frown}{AB}}{\text{m}\overset{\huge\frown}{CD}}\\\\ \text{En effet,}\quad \dfrac{90^\circ}{40^\circ} &= \dfrac{180\ \text{cm}}{80\ \text{cm}}=2{,}25 \end{align}||
Le secteur de disque représente une partie du disque ou une section de l'aire totale de celui-ci.
Il est possible de calculer l'aire d'un secteur à partir de l'angle au centre qui le forme ou de son arc de cercle.
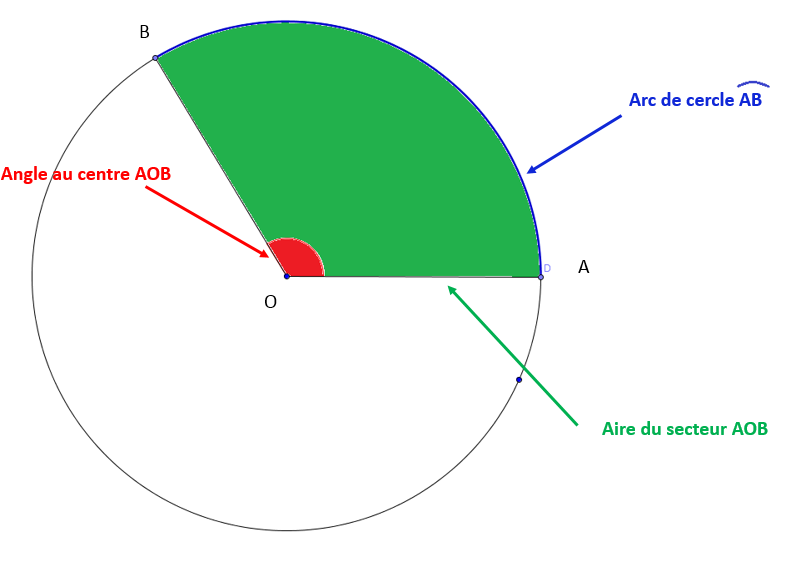
Pour trouver la superficie d'un secteur d'un disque, on peut utiliser les rapports suivants :
||\dfrac{\text{Angle au centre}}{360^\circ}=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}}||
Quelle est l'aire de cette pointe de tarte si son diamètre est de |25\ \text{cm}| et que l'angle au centre correspond à |60^\circ|?
Calcul du rayon||\begin{align} r&=\dfrac{\text{diamètre}}{2}\\&=\dfrac{25}{2}\\ &=12{,}5\ \text{cm}\end{align}||
Utilisation du rapport
||\begin{align} \dfrac{\text{Angle au centre}}{360^\circ} &=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}}\\\\ \dfrac{60^\circ}{360^\circ}&= \dfrac{\text{Aire du secteur}}{\pi (12{,}5)^2}\\\\ \dfrac{60^\circ}{360^\circ}&= \dfrac{\text{Aire du secteur}}{490{,}87\ \text{cm}^2}\\\\ \Rightarrow\ \text{Aire du secteur} &= \dfrac{60^\circ \times 490{,}87\ \text{cm}^2}{360^\circ}=81{,}81\ \text{cm}^2\end{align}||
Un secteur de disque vaut |60\ \text{cm}^2.| Quelle est la longueur de son arc de cercle |\overset{\,\huge\frown}{AB}| si le rayon du cercle est de |6\ \text{cm}|?
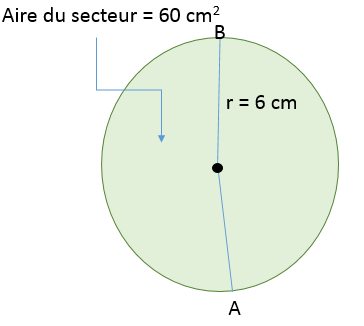
||\begin{align} \dfrac{\text{Arc de cercle}}{\text{Circonférence}}&=\dfrac{\text{Aire du secteur}}{\text{Aire du cercle}}\\[4pt] \dfrac{\text{Arc de cercle}}{2 \pi r}&=\dfrac{\text{Aire du secteur}}{\pi r^2}\\[3pt] \dfrac{\text{m}\overset{\,\huge\frown}{AB}}{2\pi (6)}&=\dfrac{60\ \text{cm}^2}{\pi (6)^2}\\[3pt] \dfrac{\text{m}\overset{\,\huge\frown}{AB}}{37{,}70\ \text{cm}}&=\dfrac{60\ \text{cm}^2}{113{,}10\ \text{cm}^2}\\[4pt] \Rightarrow\ \text{m}\overset{\,\huge\frown}{AB} &= \dfrac{37{,}70\times 60}{113{,}10}= 20\ \text{cm}\end{align}||Ainsi, |\overset{\,\huge\frown}{AB}| mesure |20\ \text{cm}.|
Dans un disque, le rapport des aires de 2 secteurs est égal au rapport des mesures des angles au centre.
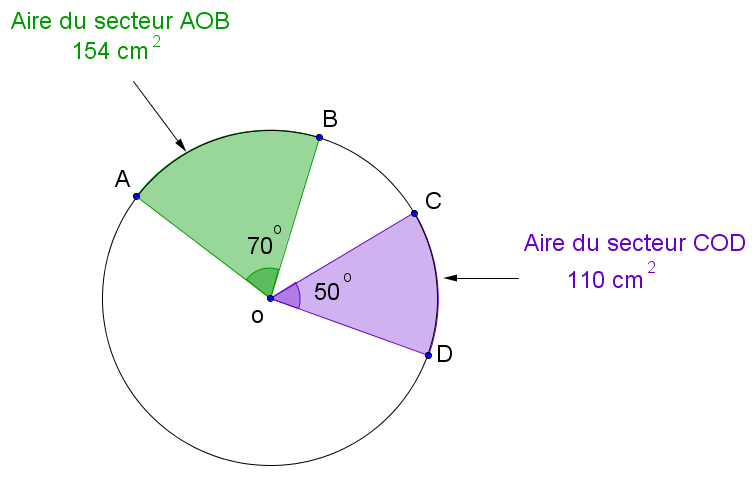
||\dfrac{\text{Aire du secteur } AOB}{\text{Aire du secteur }COD} = \dfrac{\text{m}\angle AOB}{\text{m}\angle COD}||
Pour valider ta compréhension de l'aire et du périmètre des figures planes de façon interactive, consulte la MiniRécup suivante :

