Matières
Niveaux
Les types de probabilités
Fiche | Mathématiques
Secondaire
1-5
La probabilité d'un évènement est une valeur qui quantifie la possibilité que cet évènement se produise.
La valeur d'une probabilité est toujours comprise entre |0| et |1| inclusivement. Cette valeur peut s'exprimer en pourcentage, en fraction ou en nombre décimal.
Il existe différents types de probabilités.
Les probabilités théoriques
La probabilité théorique d'un évènement est une probabilité déterminée à l’aide d’un raisonnement mathématique.
Lorsque les évènements élémentaires d'une expérience aléatoire sont équiprobables, on peut calculer la probabilité théorique de la façon suivante.
||\text{Probabilité théorique} = \dfrac{\text{Nombre de résultats favorables}}{\text{Nombre de résultats possibles}}||
-
La probabilité d’obtenir un |3| lors du lancer d'un dé à |6| faces est de |1| sur |6,| puisqu'il y a |1| résultat favorable (obtenir la face |3|) sur |6| résultats possibles (les |6| faces du dé).||P(6)=\dfrac{1}{6}||
-
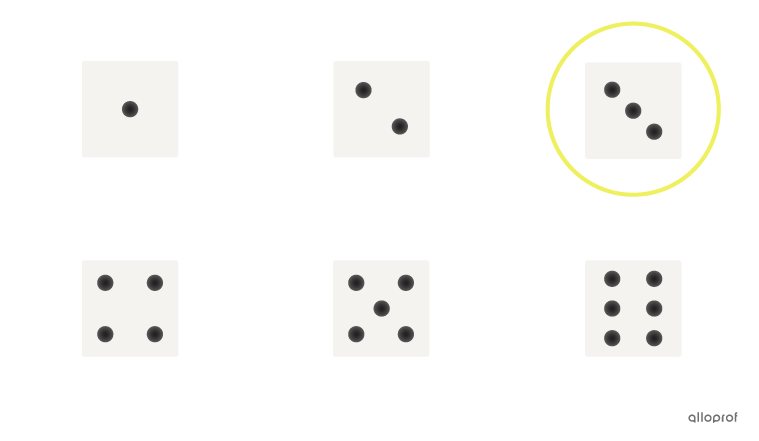
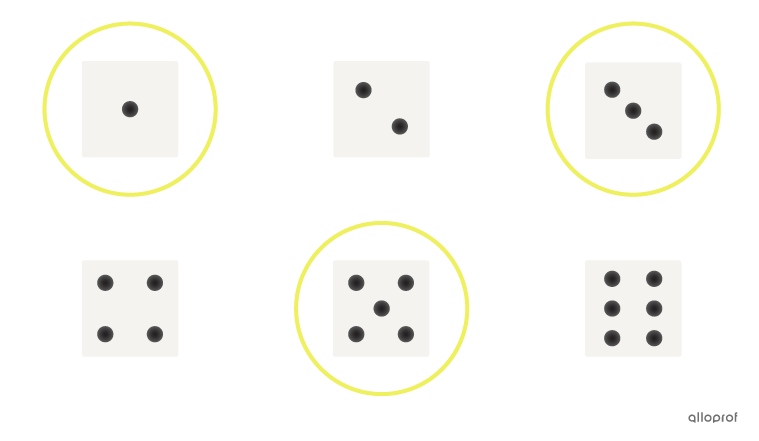
La probabilité d'obtenir un nombre impair lors du lancer d'un dé à |6| faces est de |1| sur |2,| puisqu'il y a |3| résultats favorables (|1,| |3| et |5|) sur |6| résultats possibles (les |6| faces du dé).||P(\text{obtenir un nombre impair})=\dfrac{3}{6}=\dfrac{1}{2}||
Les probabilités fréquentielles (ou expérimentales) (secondaire 2, 3, 4 et 5)
La probabilité fréquentielle (ou probabilité expérimentale) d'un évènement est une probabilité déterminée à l’aide des résultats d’une expérimentation.
La probabilité fréquentielle d’un évènement est souvent utilisée lorsque la probabilité théorique est difficile, voire impossible, à calculer. Afin de la déterminer, il est nécessaire de répéter la même expérience aléatoire un grand nombre de fois. Plus le nombre de résultats de l’expérience est grand, plus la probabilité fréquentielle de cet évènement est une bonne estimation de sa probabilité théorique.
On peut déterminer la probabilité fréquentielle d'un événement de la façon suivante.
||\text{Probabilité fréquentielle} = \dfrac{\begin{gather}\text{Nombre de fois que le}\\ \text{résultat attendu s'est réalisé}\end{gather}}{\begin{gather}\text{Nombre de fois que}\\\text{l'expérience a été répétée}\end{gather}}||
On laisse tomber un verre de plastique par terre. Quelle est la probabilité qu'il s'immobilise sur sa base ouverte?
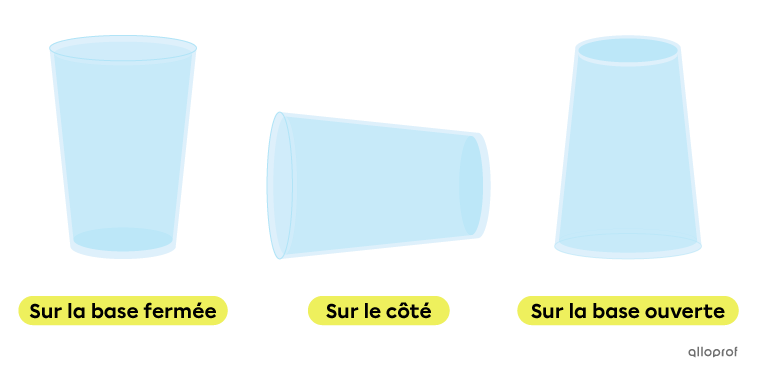
Il est très difficile de calculer la probabilité théorique de chaque évènement parce que les 3 évènements élémentaires ne sont pas nécessairement équiprobables. Pour calculer la probabilité fréquentielle du résultat désiré, il faut répéter l'expérience de nombreuses fois. Ainsi, on peut déterminer le nombre de fois que le verre tombe sur sa base ouverte par rapport au nombre de répétitions de l'expérience.
|
Lancer |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Résultat |
Côté |
Côté |
Base fermée |
Côté |
Côté |
Côté |
Base ouverte |
Côté |
Côté |
Côté |
Côté |
Base ouverte |
||\begin{align}P(\text{base ouverte})&= \dfrac{\begin{gather}\text{Nombre de fois que le}\\ \text{résultat attendu s'est réalisé}\end{gather}}{\begin{gather}\text{Nombre de fois que}\\\text{l'expérience a été répétée}\end{gather}}\\&=\dfrac{2}{12}\\&=0{,}1\overline{6}\end{align}||Donc, si on lance le verre une autre fois, on peut supposer qu’il a |16{,}\overline{6}\ \%| de chance de s’immobiliser sur sa base ouverte.
Même si un des résultats n'est pas observé lors de l'expérience aléatoire, on ne peut pas conclure que ce résultat est impossible.
La comparaison entre une probabilité théorique et une probabilité fréquentielle
Quelle est la probabilité d’obtenir le côté « face » lors du lancer d’une pièce de monnaie?
La probabilité théorique
Si la pièce de monnaie n’est pas truquée, alors les |2| évènements (obtenir « face » et obtenir « pile ») sont équiprobables.||\begin{align}P(\text{obtenir « face »})&=\dfrac{1}{2}\\&=50\ \%\end{align}||
La probabilité fréquentielle
Si on soupçonne que la pièce de monnaie est truquée, on ne peut pas calculer les probabilités théoriques. On fait |35| lancers avec la pièce de monnaie. On obtient |16| fois « face » et |19| fois « pile ».||\begin{align}P(\text{obtenir « face »})&=\dfrac{16}{35}\\&\approx 45{,}7\ \%\end{align}||Plus on répète l'expérience, plus on devrait se rapprocher de |50\ \%,| soit la probabilité théorique. Si ce n’est pas le cas, c'est que la pièce est bel et bien truquée.
Les probabilités subjectives (secondaire 4 et 5)
La probabilité subjective d'un évènement est une probabilité déterminée à l’aide d’un jugement personnel.
Dans certaines situations, on n’a pas assez d’informations pour déterminer la probabilité théorique ou la probabilité fréquentielle d’un événement. Il faut alors se baser sur nos observations ainsi que sur notre jugement pour déterminer cette probabilité. On parle alors de probabilité subjective, puisqu'elle peut être différente d'une personne à l'autre.
-
Julien estime la probabilité de réussir son prochain examen de mathématiques à |90\ \%,| puisqu'il juge qu'il a beaucoup étudié.
-
En analysant les statistiques, on estime que les Canadiens de Montréal ont |50\ \%| de chance de gagner la coupe Stanley cette année.
-
Les nuages sont gris et l’air est humide, alors on estime qu’il y a |80\ \%| de chance qu’il pleuve.