Matières
Niveaux
Il arrive qu'on s'intéresse à la probabilité associée à 2 choix possibles dans une expérience aléatoire. Selon la formulation de la question, il y a 2 calculs possibles.
Si on cherche la probabilité d’un choix ou d’un autre choix, on additionne les probabilités de chaque choix possible.
Si on cherche la probabilité d’un choix et d’un autre choix, on multiplie les probabilités de chaque choix possible.
Dans une expérience aléatoire à une ou plusieurs étapes, il faut additionner les probabilités lorsqu’on s’intéresse à un choix ou à un autre. Dans un diagramme en arbre, cette situation est représentée par 2 branches d’une même étape.
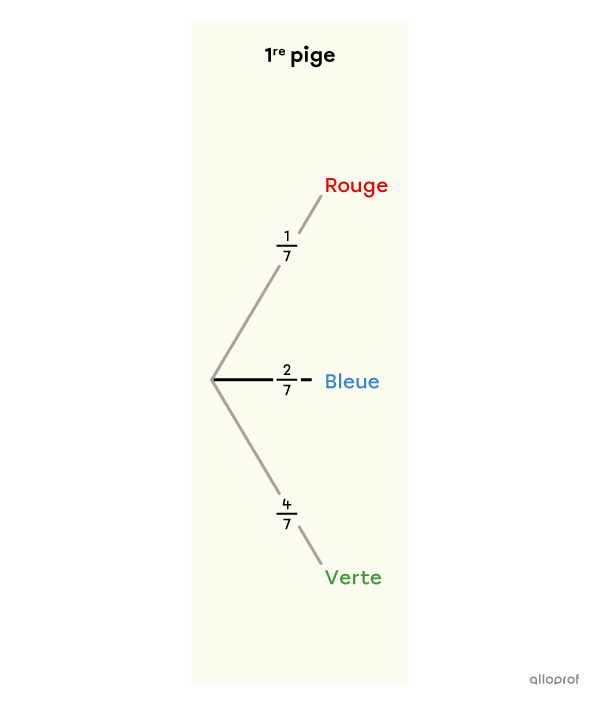
On pige une bille dans un sac contenant |1| bille rouge, |2| billes bleues et |4| billes vertes. Quelle est la probabilité de l'évènement « piger une bille rouge ou une bille verte »?
On fait le diagramme en arbre.
Dans cette expérience aléatoire à une étape, l’évènement fait intervenir 2 des choix possibles. Pour déterminer la probabilité de l’évènement, il faut donc additionner les probabilités de ces 2 choix.||\begin{align}P(\text{rouge ou verte})&=P(\text{rouge})+P(\text{verte})\\&= \dfrac{1}{7} + \dfrac{4}{7}\\&= \dfrac{5}{7}\end{align}||
Réponse : La probabilité de piger une bille rouge ou une bille verte est de |\dfrac{5}{7},| soit environ |71\ \%.|
Il arrive que l’énoncé d’un évènement ne contienne pas le mot « ou », mais qu’on doive quand même additionner des probabilités pour trouver la probabilité recherchée.
On lance un dé à |6| faces. Quelle est la probabilité de l'évènement « obtenir un nombre premier »?
Les nombres premiers se trouvant sur un dé à |6| faces sont |2,| |3| et |5.| Ainsi, cela revient à s’intéresser à la probabilité de l’évènement « obtenir un |2| ou un |3| ou un |5| ».||\begin{align}P(\text{nombre premier})&=P(\text{obtenir un}\ 2)+P(\text{obtenir un}\ 3)+P(\text{obtenir un}\ 5)\\&= \dfrac{1}{6} + \dfrac{1}{6} +\dfrac{1}{6}\\&= \dfrac{3}{6}\\&=\dfrac{1}{2}\end{align}||
Réponse : La probabilité d’obtenir un nombre premier est de |\dfrac{1}{2},| soit |50\ \%.|
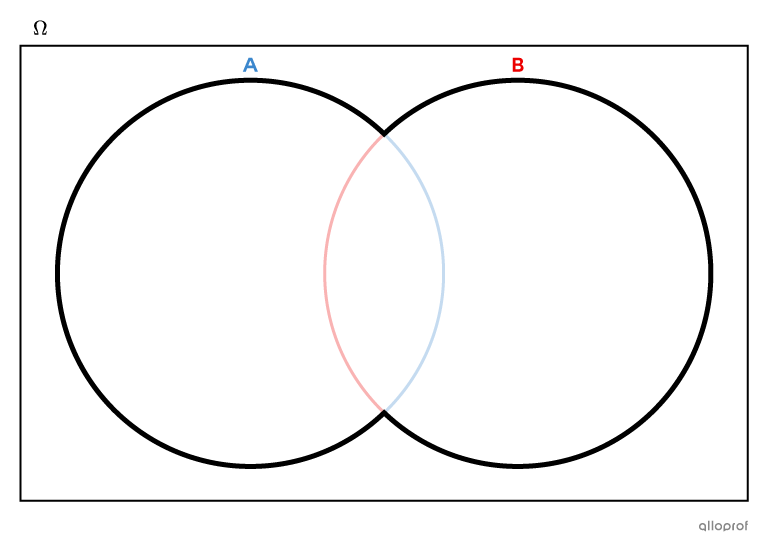
Dans un diagramme de Venn, la notion du « ou » est associée à l’union d’ensembles. En effet, pour déterminer quels sont les éléments qui font partie de |A| ou de |B,| il faut s’intéresser à |A \cup B.| On doit compter les éléments qui font seulement partie de |A,| ceux qui font seulement partie de |B| et ceux qui font partie de l’intersection de |A| et de |B| |(A \cap B).|
Dans une classe de |32| élèves, il y en a |12| qui jouent seulement au hockey, |7| qui jouent seulement au baseball et |4| qui jouent à la fois au hockey et au baseball. Les autres élèves de la classe pratiquent d’autres sports. Si on choisit un élève au hasard, quelle est la probabilité que cet élève joue au hockey ou au baseball?
On construit le diagramme de Venn associé à cette situation.
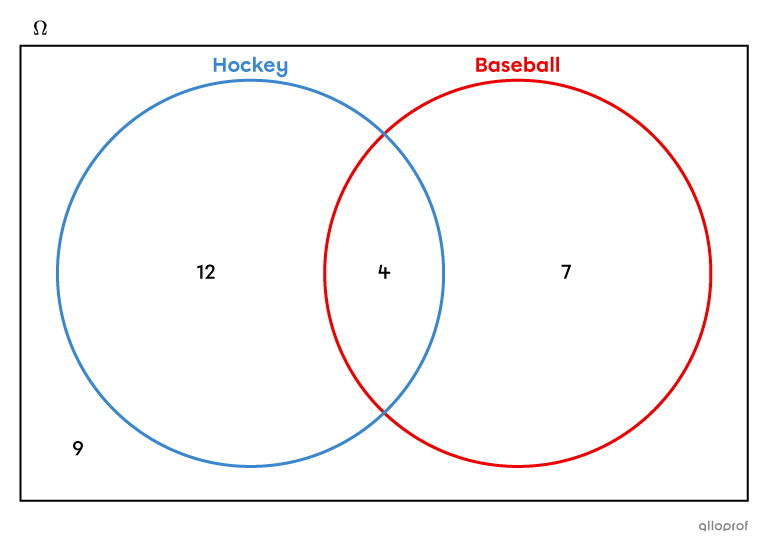
Pour trouver la probabilité de choisir au hasard un élève qui joue au hockey ou au baseball, on doit additionner le nombre d’élèves qui jouent seulement au hockey, qui jouent seulement au baseball et qui pratiquent les 2 sports.||\begin{align}P(\text{hockey ou baseball})&=\dfrac{12+4+7}{32}\\&=\dfrac{23}{32}\\&\approx 0{,}72\end{align}||
Réponse : La probabilité de choisir au hasard un élève qui joue au hockey ou au baseball est de |\dfrac{23}{32},| soit environ |72\ \%.|
Dans une expérience aléatoire à plusieurs étapes, il faut multiplier les probabilités lorsqu’on s’intéresse à un choix suivi d’un autre. Dans un diagramme en arbre, cette situation est représentée par 2 branches bout à bout.
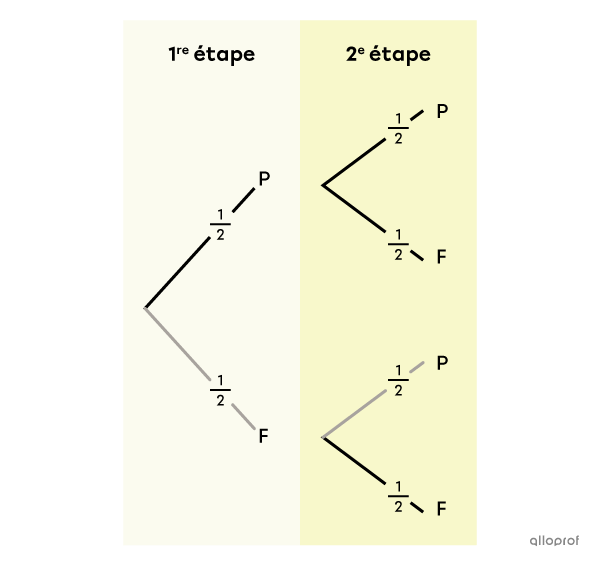
On lance 2 fois une pièce de monnaie. Quelle est la probabilité d'obtenir « face » (F) et « pile » (P), si on tient compte de l’ordre?
On fait le diagramme en arbre.
Il s’agit d’une expérience à |2| étapes. On cherche |P(\text{F},\text{P}).| On multiplie donc la probabilité d’obtenir « face » au 1er lancer par la probabilité d’obtenir « pile » au 2e lancer.||\begin{align}P(\text{F},\text{P})&=\dfrac{1}{2} \times \dfrac{1}{2}\\ &= \dfrac{1}{4}\end{align}||
Réponse : La probabilité d’obtenir « face » au 1er lancer et « pile » au 2e lancer est de |\dfrac{1}{4},| soit |25\ \%.|
L’utilisation du mot « et » peut prendre plusieurs sens, selon si on doit tenir compte de l’ordre ou non dans l’expérience aléatoire. C’est pourquoi il est important de bien analyser la question pour y répondre adéquatement.
Dans l’exemple précédent, si on s’était intéressé au même évènement, mais sans tenir compte de l’ordre, la réponse aurait été différente. En effet, |(\text{F},\text{P})| et |(\text{P},\text{F})| aurait été tous les |2| des résultats favorables à cet évènement. Il aurait donc fallu trouver la probabilité pour ces |2| résultats, puis les additionner.
Un sac contient |1| bille rouge |(R),| |2| billes bleues |(B)| et |4| billes vertes |(V).| On pige |1| bille dans ce sac, puis on la remet dans le sac. On pige ensuite une 2e bille.
Quelle est la probabilité de l'événement « piger une bille bleue et une bille verte » si on ne tient pas compte de l’ordre?
On fait le diagramme en arbre.
Pour trouver la probabilité de cet évènement, on trouve d’abord la probabilité de piger une bille bleue suivie d’une bille verte et celle de piger une bille verte suivie d’une bille bleue. ||\begin{align}P(B,V)&=P(B) \times P(V)\\&= \dfrac{2}{7} \times \dfrac{4}{7}\\&= \dfrac{8}{49}\\\\P(V,B)&=P(V) \times P(B)\\&= \dfrac{4}{7} \times \dfrac{2}{7}\\&= \dfrac{8}{49}\end{align}||On additionne ensuite ces 2 probabilités.||\begin{align}P(B\text{ et }V)&=P(B,V)+P(V,B)\\&=\dfrac{8}{49}+\dfrac{8}{49}\\&=\dfrac{16}{49}\end{align}||
Réponse : La probabilité de piger une bille bleue et une bille verte est de |\dfrac{16}{49},| soit environ |33\ \%.|
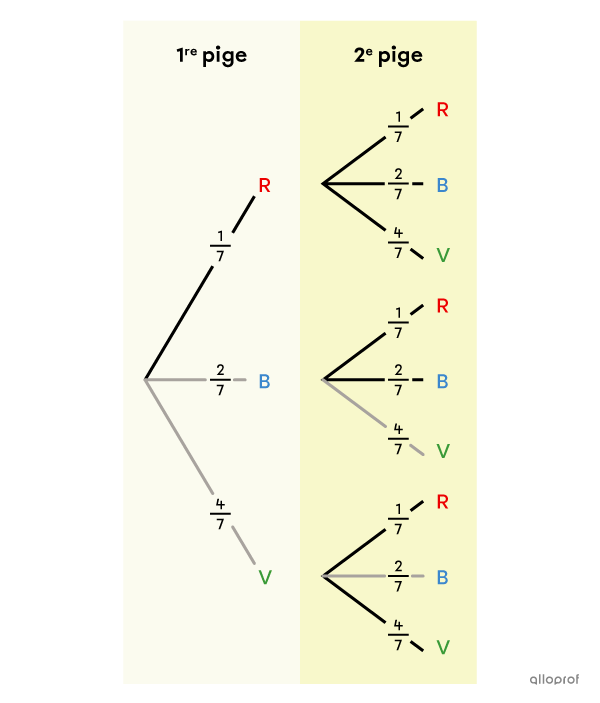
Dans un diagramme de Venn, la notion du « et » est associée à l’intersection. En effet, pour déterminer les éléments qui font partie de |A| et de |B,| il faut s’intéresser à |A \cap B.|
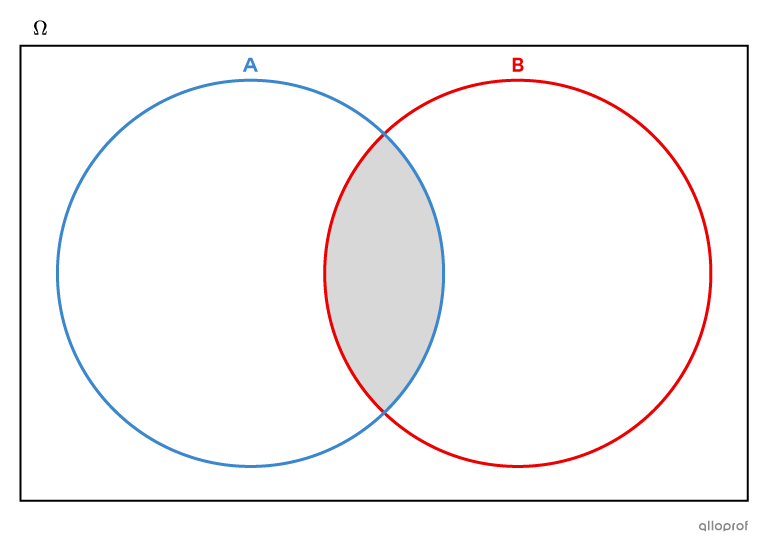
Dans une classe de |32| élèves, il y en a |12| qui jouent seulement au hockey, |7| qui jouent seulement au baseball et |4| qui jouent à la fois au hockey et au baseball. Les autres élèves de la classe font d’autres sports. Si on choisit un élève au hasard, quelle est la probabilité que cet élève joue au hockey et au baseball?
On construit le diagramme de Venn associé à cette situation.
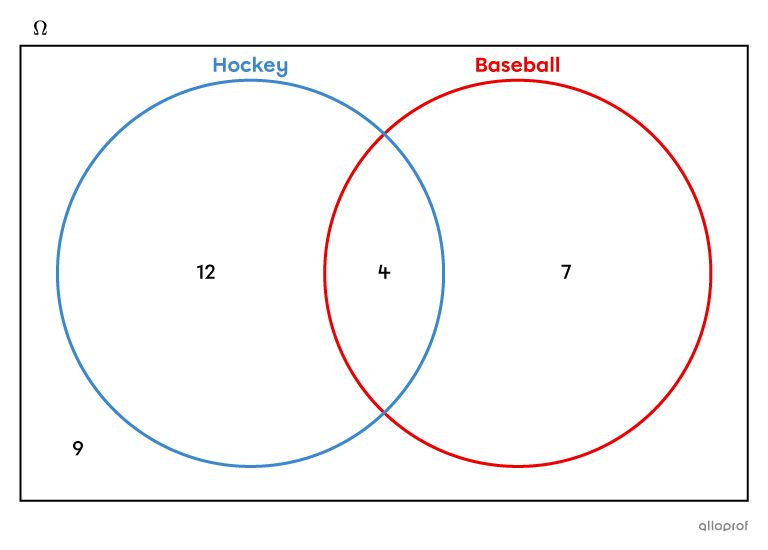
Pour trouver la probabilité de choisir au hasard un élève qui joue au hockey et au baseball, on doit prendre en considération l’intersection des ensembles, c’est-à-dire uniquement les élèves qui pratiquent les 2 sports.||\begin{align}P(\text{hockey et baseball})&=\dfrac{4}{32}\\&=\dfrac{1}{8}\end{align}||
Réponse : La probabilité de choisir au hasard un élève qui joue au hockey et au baseball est de |\dfrac{1}{8},| soit |12{,}5\ \%.|
Pour répondre à une question, il arrive qu’on doive utiliser les notions du « et » et du « ou » . Dans ce cas, on commence par utiliser la multiplication pour déterminer la probabilité d’un résultat issu d’une expérience aléatoire à plusieurs étapes, puis on utilise l’addition.
On fait tourner 2 roulettes. La 1re roulette est séparée en |3| parties, identifiées par les chiffres de |1| à |3.| La 2e roulette est séparée en |4| parties, identifiées par les lettres |A,| |B,| |C| et |D.|
Sur la 1re roulette, la section |1| et la section |2| occupent chacune un quart de la roulette, alors que la section |3| en occupe la moitié. Sur la 2e roulette, les sections |A| et |C| occupent chacune un quart de la roulette, la section |B| en occupe le huitième et la section |D|, les |3| huitièmes.
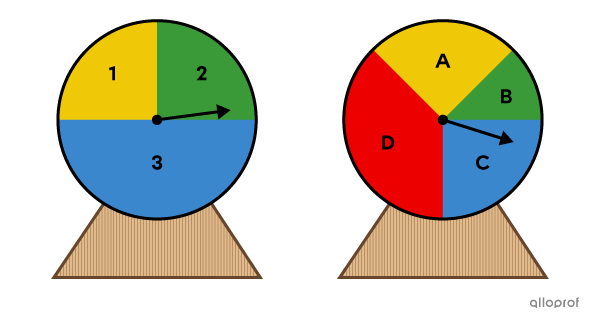
Quelle est la probabilité d’obtenir |1| et |A| ou d’obtenir |3| et |D|?

Moments dans la vidéo :