Matières
Niveaux
Une identité trigonométrique est une égalité, toujours vraie, découlant de certaines relations entre divers rapports trigonométriques.


À partir du triangle rectangle, il est possible de définir différents rapports trigonométriques que l'on peut ensuite transposer dans le cercle trigonométrique.

||\sin\theta=\dfrac{\color{#ec0000}y}{\color{#3a9a38}1}=y||Le sinus d’un angle |\theta| est associé à l’ordonnée (la coordonnée |y|) du point trigonométrique |P(\theta).|
||\cos\theta=\dfrac{\color{#333fb1}x}{\color{#3a9a38}1}=x||Le cosinus d’un angle |\theta| est associé à l’abscisse (la coordonnée |x|) du point trigonométrique |P(\theta).|
||\tan\theta=\dfrac{\sin\theta}{\cos\theta}=\dfrac{\color{#ec0000}y}{\color{#333fb1}x}||La tangente d’un angle |\theta| est associée au rapport de l’ordonnée |(y)| et de l’abscisse |(x)| du point trigonométrique |P(\theta).|
Les 3 rapports suivants sont les inverses multiplicatifs des 3 rapports précédents.
Le rapport cosécante d’un angle |\theta| est l’inverse du sinus de l’angle |\theta.|||\text{cosec}\ \theta=\dfrac{1}{\sin\theta}||
Le rapport sécante d’un angle |\theta| est l’inverse du cosinus de l’angle |\theta.|||\text{sec}\ \theta=\dfrac{1}{\cos\theta}||
Le rapport cotangente d’un angle |\theta| est l’inverse de la tangente de l’angle |\theta.|||\text{cotan}\ \theta=\dfrac{\cos\theta}{\sin\theta}=\dfrac{1}{\tan\theta}||
Remarque : On peut utiliser |\csc| ou |\text{cosec}| comme notation pour la cosécante et |\cot| ou |\text{cotan}| comme notation pour la cotangente.
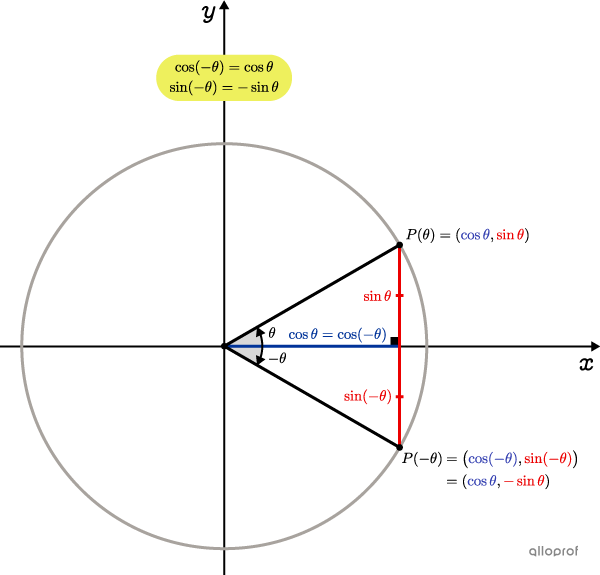
La coordonnée |x| du point |P(-\theta)| est la même que celle du point |P(\theta).| La coordonnée |y| de |P(-\theta)| est l’opposé de celle de |P(\theta).|
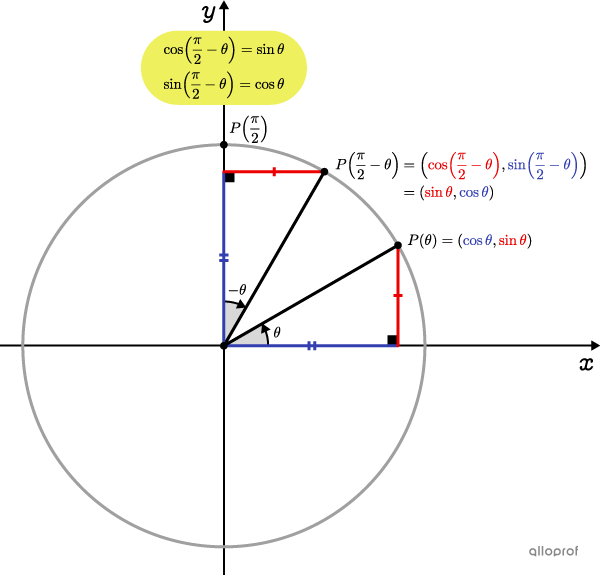
La coordonnée |x| du point |P\left(\dfrac{\pi}{2}-\theta\right)| est la coordonnée |y| du point |P(\theta).| De la même façon, la coordonnée |y| de |P\left(\dfrac{\pi}{2}-\theta\right)| est la coordonnée |x| de |P(\theta).|
Voici comment procéder pour déterminer la valeur d’une expression trigonométrique en n’utilisant que la définition des rapports.
Déterminer les coordonnées du point trigonométrique |P(\theta).|
Modifier l’expression en termes de |\sin\theta| et/ou de |\cos\theta.|
Remplacer les coordonnées dans l’expression.
Déterminer la valeur de l’expression.
Détermine la valeur exacte de l’expression trigonométrique |\tan\left(\dfrac{2\pi}{3}\right).|
Déterminer les coordonnées du point trigonométrique |\boldsymbol{P(\theta)}|
||P\left(\dfrac{2\pi}{3}\right)=\left(\color{#333fb1}{-\dfrac{1}{2}},\color{#ec0000}{\dfrac{\sqrt{3}}{2}}\right)||
Modifier l’expression en termes de |\boldsymbol{\sin\theta}| et/ou de |\boldsymbol{\cos\theta}|
||\tan\left(\dfrac{2\pi}{3}\right)=\dfrac{\sin\left(\dfrac{2\pi}{3}\right)}{\cos\left(\dfrac{2\pi}{3}\right)}||
Remplacer les coordonnées dans l’expression
||\tan\left(\dfrac{2\pi}{3}\right)=\dfrac{\color{#ec0000}{\dfrac{\sqrt{3}}{2}}}{\color{#333fb1}{-\dfrac{1}{2}}}||
Déterminer la valeur de l’expression
||\begin{align}\tan\left(\dfrac{2\pi}{3}\right)&=\dfrac{\sqrt{3}}{2}\times-\dfrac{2}{1}\\&=-\dfrac{2\sqrt{3}}{2}\\&=-\sqrt{3}\end{align}||
Réponse : La valeur exacte de |\tan\left(\dfrac{2\pi}{3}\right)| est |-\sqrt{3}.|
Détermine la valeur exacte de l’expression |\sec\left(\dfrac{5\pi}{4}\right).|
Déterminer les coordonnées du point trigonométrique |\boldsymbol{P(\theta)}|
||P\left(\dfrac{5\pi}{4}\right)=\left(\color{#333fb1}{-\dfrac{\sqrt{2}}{2}},\color{#ec0000}{-\dfrac{\sqrt{2}}{2}}\right)||
Modifier l’expression en termes de |\boldsymbol{\sin\theta}| et/ou de |\boldsymbol{\cos\theta}|
||\sec\left(\dfrac{5\pi}{4}\right)=\dfrac{1}{\cos\left(\dfrac{5\pi}{4}\right)}||
Remplacer les coordonnées dans l’expression
||\sec\left(\dfrac{5\pi}{4}\right)=\dfrac{1}{\color{#333fb1}{-\dfrac{\sqrt{2}}{2}}}||
Déterminer la valeur de l’expression
||\begin{align}\sec\left(\dfrac{5\pi}{4}\right)&=1\times-\dfrac{2}{\sqrt{2}}\\&=-\dfrac{2}{\sqrt{2}}\end{align}||On doit rationaliser la fraction pour ne pas avoir de racine au dénominateur.||\begin{align}\sec\left(\dfrac{5\pi}{4}\right)&=-\dfrac{2}{\sqrt{2}}\color{#ec0000}{\times\dfrac{\sqrt{2}}{\sqrt{2}}}\\&=-\dfrac{2\sqrt{2}}{2}\\&=-\sqrt{2}\end{align}||
Réponse : La valeur exacte de |\sec\left(\dfrac{5\pi}{4}\right)| est |-\sqrt{2}.|
Il est possible qu'un angle soit plus grand que |2 \pi\ \text{rad}| |(360^\circ),| ce qui correspond à plus d’une rotation autour du cercle trigonométrique. Lorsqu’on veut savoir à quoi correspond un angle dans l’intervalle |[0,2\pi],| il faut enlever un certain nombre de rotations de |2\pi| pour trouver le point du cercle équivalent.
Voici les étapes à suivre pour évaluer une expression trigonométrique dont l'angle n'est pas dans l'intervalle |[0,2\pi].|
Calculer le nombre de rotations à soustraire à l’angle |\theta| en divisant cette mesure d’angle par |2\pi| et en conservant la partie entière du résultat obtenu.||N=\left[\dfrac{\theta}{2\pi}\right]||
À partir de l’angle |\theta,| soustraire l’angle formé par le nombre de rotations calculé |(N).|||\theta\, '=\theta-(N\times 2\pi)||
Situer le résultat, qui est un angle entre |0| et |2\pi,| sur le cercle trigonométrique et indiquer ses coordonnées |x| et |y.|
Déterminer la valeur de l’expression trigonométrique recherchée à l’aide de ses coordonnées.
Détermine la valeur exacte de |\text{cosec}\left(\dfrac{47\pi}{6}\right).|
Calculer le nombre de rotations
||\begin{align}N&=\left[\dfrac{\theta}{2\pi}\right]\\&=\left[\dfrac{\frac{47\pi}{6}}{2\pi}\right]\\&=\left[\dfrac{47\pi}{6}\times\dfrac{1}{2\pi}\right]\\&=\left[\dfrac{47}{12}\right]\\&=\left[3{,}91\overline{6}\right]\\&=3\end{align}||
Soustraire l’angle formé par les rotations
||\begin{align}\theta\, '&=\color{#3a9a38}\theta-(\color{#3a9a38}N\times2\pi)\\&=\color{#3a9a38}{\dfrac{47\pi}{6}}-(\color{#3a9a38}3\times2\pi)\\&=\dfrac{47\pi}{6}-6\pi\\&=\dfrac{47\pi}{6}-\dfrac{36\pi}{6}\\&=\dfrac{11\pi}{6}\end{align}||
Trouver les coordonnées
Le point |P\left(\dfrac{47\pi}{6}\right)| coïncide avec le point |P\left(\dfrac{11\pi}{6}\right).| Ses coordonnées sont donc les suivantes.||\begin{align}P\left(\dfrac{47\pi}{6}\right)&=P\left(\dfrac{11\pi}{6}\right)\\&=\left(\color{#333fb1}{\dfrac{\sqrt{3}}{2}},\color{#ec0000}{-\dfrac{1}{2}}\right)\end{align}||
Déterminer la valeur de l’expression
||\begin{align}\text{cosec}\left(\dfrac{47\pi}{6}\right)&=\dfrac{1}{\color{#ec0000}{\sin\left(\dfrac{47\pi}{6}\right)}}\\&=\dfrac{1}{\color{#ec0000}{-\dfrac{1}{2}}}\\&=1\times-\dfrac{2}{1}\\&=-2\end{align}||
Réponse : La valeur exacte de |\text{cosec}\left(\dfrac{47\pi}{6}\right)| est |-2.|
Calcule la valeur de |\text{cotan}\left(-\dfrac{79\pi}{3}\right).|
Calculer le nombre de rotations
||\begin{align}N&=\left[\dfrac{\theta}{2\pi}\right]\\&=\left[\dfrac{-\frac{79\pi}{3}}{2\pi}\right]\\&=\left[-\dfrac{79\pi}{3}\times\dfrac{1}{2\pi}\right]\\&=\left[-\dfrac{79}{6}\right]\\&=\left[-13{,}1\overline{6}\right]\\&=-14\end{align}||Ici, on doit déterminer la partie entière d’un nombre négatif. On obtient donc un nombre de tours négatif. Cela signifie que l’angle de rotation pour déterminer le nombre de tours est dans le sens horaire.
Soustraire l’angle formé par les rotations
||\begin{align}\theta\ '&=\color{#3a9a38}\theta-(\color{#3a9a38}N\times2\pi)\\&=\color{#3a9a38}{-\dfrac{79\pi}{3}}-(\color{#3a9a38}{-14}\times2\pi)\\&=-\dfrac{79\pi}{3}+28\pi\\&=-\dfrac{79\pi}{3}+\dfrac{84\pi}{3}\\&=\dfrac{5\pi}{3}\end{align}||
Trouver les coordonnées
Le point |P\left(-\dfrac{79\pi}{3}\right)| coïncide avec le point |P\left(\dfrac{5\pi}{3}\right).| Ses coordonnées sont donc les suivantes.||\begin{align}P\left(-\dfrac{79\pi}{3}\right)&=P\left(\dfrac{5\pi}{3}\right)\\&=\left(\color{#333fb1}{\dfrac{1}{2}},\color{#ec0000}{-\dfrac{\sqrt{3}}{2}}\right)\end{align}||
Déterminer la valeur de l’expression
||\begin{align}\text{cotan}\left(-\dfrac{79\pi}{3}\right)&=\text{cotan}\left(\dfrac{5\pi}{3}\right)\\&=\dfrac{\color{#333fb1}{\cos\left(\dfrac{5\pi}{3}\right)}}{\color{#ec0000}{\sin\left(\dfrac{5\pi}{3}\right)}}\\&=\dfrac{\color{#333fb1}{\dfrac{1}{2}}}{\color{#ec0000}{-\dfrac{\sqrt{3}}{2}}}\\&=\dfrac{1}{2}\times-\dfrac{2}{\sqrt{3}}\\&=-\dfrac{1}{\sqrt{3}}\\&=-\dfrac{1}{\sqrt{3}}\times\dfrac{\sqrt{3}}{\sqrt{3}}\\&=-\dfrac{\sqrt{3}}{3}\end{align}||
Réponse : La valeur exacte de |\text{cotan}\left(-\dfrac{79\pi}{3}\right)| est |-\dfrac{\sqrt{3}}{3}.|
Les identités trigonométriques pythagoriciennes sont utiles dans les démonstrations d’identités trigonométriques.
||\begin{alignat}{13}\cos^2\theta\ \,&+\,\sin^2\theta&&=\quad\ 1\\1\quad\ \,&+\tan^2\theta&&=\ \sec^2\theta\\\text{cotan}^2\theta&+\quad1&&=\text{cosec}^2\theta\end{alignat}||
Voici les démonstrations des 3 identités pythagoriciennes.
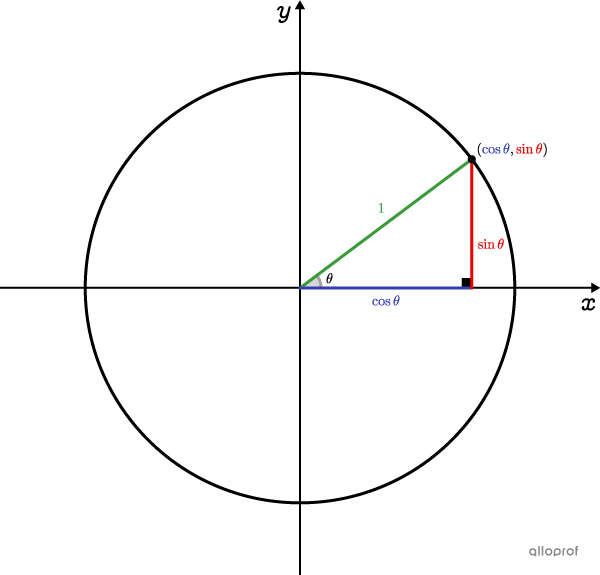
En utilisant le cercle trigonométrique et le théorème de Pythagore, on obtient la 1re identité pythagoricienne.||\begin{align}\color{#333fb1}a^2 + \color{#ec0000}b^2 &=\color{#3a9a38}c^2\\ \color{#333fb1}{(\cos\theta)}^2 + \color{#ec0000}{(\sin\theta)}^2 &=\color{#3a9a38}{(1)}^2\\ \cos^2 \theta + \sin^2 \theta &=1 \end{align}||Si on divise tous les termes de l'égalité précédente par |\cos^2 \theta,| on obtient la 2e identité. ||\begin{align}\dfrac{\cos^2 \theta}{\cos^2 \theta} + \dfrac{\sin^2 \theta}{\cos^2 \theta} &= \dfrac{1}{\cos^2\theta}\\\\ 1 + \tan^2 \theta &= \sec^2 \theta\end{align}||Si on divise tous les termes de la 1re identité par |\sin^2 \theta,| on obtient la 3e identité. ||\begin{align}\dfrac{\cos^2 \theta}{\sin^2 \theta} + \dfrac{\sin^2 \theta}{\sin^2 \theta} &= \dfrac{1}{\sin^2\theta}\\\\\text{cotan}^2 \theta + 1 &= \text{cosec}^2 \theta\end{align}||
Remarque : |\cos^2 \theta = (\cos\theta)^2.| C’est la même chose pour les autres rapports trigonométriques.
||\begin{align}\sin(A+B)&=\sin A\cos B+\cos A\sin B\\\\
\sin(A-B)&=\sin A\cos B-\cos A\sin B\\\\ \sin(2A)&=2 \sin A \cos A \end{align}||
||\begin{align}\cos(A+B)&=\cos A\cos B-\sin A\sin B\\\\
\cos(A-B)&=\cos A\cos B+\sin A\sin B\\\\ \cos(2A)&=\cos^2A-\sin^2 A\end{align}||
||\begin{align}\tan(A+B)&=\dfrac{\tan A+\tan B}{1-\tan A\tan B}\\\\\tan(A-B)&=\dfrac{\tan A -\tan B}{1+\tan A \tan B}\\\\ \tan(2A)&=\dfrac{2 \tan A}{1-\tan^2A}\end{align}||
Les identités |\tan(A+B),| |\tan(A-B)| et |\tan(2A)| sont valides uniquement lorsque le dénominateur est non nul.
||1-\tan A\tan B\ne0||
||1+\tan A \tan B\ne0||
||1-\tan^2A\ne0||
Toutes ces identités sont utiles pour déterminer la valeur exacte d’une expression lorsque l’angle n’est pas un angle remarquable.
Déterminer quelle combinaison d’angles remarquables permet d’obtenir |\theta.|
Choisir la bonne identité trigonométrique.
Déterminer la valeur de l’expression.
Détermine la valeur exacte de |\sin\left(\dfrac{7\pi}{12}\right).|
Déterminer quelle combinaison d’angles remarquables permet d’obtenir |\boldsymbol{\theta}|
La valeur |\dfrac{7\pi}{12}| n'étant pas un angle remarquable, on doit la décomposer en une somme ou en une différence d'angles remarquables. On trouve l’addition suivante.||\begin{align}\dfrac{7\pi}{12}&=\dfrac{3\pi}{12}+\dfrac{4\pi}{12}\\\\&=\dfrac{\pi}{4}+\dfrac{\pi}{3}\end{align}||
Choisir la bonne identité trigonométrique
On cherche |\sin\left(\dfrac{\pi}{4}+\dfrac{\pi}{3}\right).| Il faut donc utiliser l’identité |\sin(A+B)=\sin A \cos B + \cos A \sin B| avec |A=\dfrac{\pi}{4}| et |B=\dfrac{\pi}{3}.|
Déterminer la valeur de l’expression
||\begin{align}\sin\left(\dfrac{\pi}{4}+\dfrac{\pi}{3}\right)&=\sin \dfrac{\pi}{4} \times \cos\dfrac{\pi}{3}+ \cos\dfrac{\pi}{4} \times \sin\dfrac{\pi}{3}\\\\&=\dfrac{\sqrt{2}}{2} \times \dfrac{1}{2} + \dfrac{\sqrt{2}}{2} \times \dfrac{\sqrt{3}}{2}\\\\&=\dfrac{\sqrt{2}}{4} + \dfrac{\sqrt{6}}{4}\\\\&=\dfrac{\sqrt{2}+\sqrt{6}}{4}\end{align}||
Réponse : La valeur exacte de |\sin\left(\dfrac{7\pi}{12}\right)| est |\dfrac{\sqrt{2}+\sqrt{6}}{4}.|
Détermine la valeur exacte de |\cos\left(\dfrac{\pi}{12}\right).|
Déterminer quelle combinaison d’angles remarquables permet d’obtenir |\boldsymbol{\theta}|
La valeur |\dfrac{\pi}{12}| n'étant pas un angle remarquable, on doit la décomposer en une somme ou en une différence d'angles remarquables. On trouve la soustraction suivante.||\begin{align}\dfrac{\pi}{12}&=\dfrac{4\pi}{12}-\dfrac{3\pi}{12}\\&= \dfrac{\pi}{3}-\dfrac{\pi}{4}\end{align}||
Choisir la bonne formule
On cherche |\cos\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right).| Il faut donc utiliser l’identité |\cos(A-B)=\cos A \cos B+\sin A \sin B| avec |A=\dfrac{\pi}{3}| et |B=\dfrac{\pi}{4}.|
Déterminer la valeur de l’expression
||\begin{align}\cos\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right)&=\cos\dfrac{\pi}{3} \times \cos\dfrac{\pi}{4} + \sin \dfrac{\pi}{3} \times \sin\dfrac{\pi}{4}\\\\&=\dfrac{1}{2} \times \dfrac{\sqrt2}{2} + \dfrac{\sqrt{3}}{2} \times \dfrac{\sqrt2}{2} \\\\&=\dfrac{\sqrt2}{4}+\dfrac{\sqrt6}{4}\\\\&=\dfrac{\sqrt2+\sqrt6}{4}\end{align}||
Réponse : La valeur exacte de |\cos\left(\dfrac{\pi}{12}\right)| est |\dfrac{\sqrt2+\sqrt6}{4}.|
Le résultat des 2 derniers exemples est le même. La valeur exacte de |\sin\left(\dfrac{7\pi}{12}\right)| est la même que celle de |\cos\left(\dfrac{\pi}{12}\right).| Il est possible d’expliquer ce résultat à l’aide de 2 propriétés de base des rapports |\sin| et |\cos,| soit |\sin\left(\dfrac{\pi}{2}-\theta\right)=\cos\theta| et |\cos(-\theta)=\cos\theta.|||\begin{align}\sin\left(\dfrac{7\pi}{12}\right)&=\cos\left(\dfrac{\pi}{12}\right)\\\\ \sin\left(\dfrac{6\pi}{12}+\dfrac{\pi}{12}\right)&=\cos\left(\dfrac{\pi}{12}\right)\\\\\sin\left(\dfrac{\pi}{2}-\left(-\dfrac{\pi}{12}\right)\right)&=\cos\left(\dfrac{\pi}{12}\right)\\\\\cos\left(-\dfrac{\pi}{12}\right)&=\cos\left(\dfrac{\pi}{12}\right)\\\\\cos\left(\dfrac{\pi}{12}\right)&=\cos\left(\dfrac{\pi}{12}\right)\end{align}||
Détermine la valeur exacte de |\tan\left(\dfrac{23\pi}{12}\right).|
Déterminer quelle combinaison d’angles remarquables permet d’obtenir |\boldsymbol{\theta}|
La valeur |\dfrac{23\pi}{12}| n'étant pas un angle remarquable, on doit la décomposer en une somme ou en une différence d'angles remarquables. On trouve l’addition suivante.||\begin{align}\dfrac{23\pi}{12}&=\dfrac{21\pi}{12}+\dfrac{2\pi}{12}\\\\&=\dfrac{7\pi}{4}+\dfrac{\pi}{6}\end{align}||
Choisir la bonne formule
On cherche |\tan\left(\dfrac{7\pi}{4}+\dfrac{\pi}{6}\right).| Il faut donc utiliser l’identité |\tan(A+B)=\dfrac{\tan A + \tan B}{1- \tan A \tan B}| avec |A=\dfrac{7\pi}{4}| et |B=\dfrac{\pi}{6}.|
Déterminer la valeur de l’expression
||\begin{align}\tan\left(\dfrac{7\pi}{4}+\dfrac{\pi}{6}\right)&= \dfrac{\tan\dfrac{7\pi}{4} + \tan\dfrac{\pi}{6}}{1 - \tan \dfrac{7\pi}{4} \times \tan \dfrac{\pi}{6}}\\\\&=\dfrac{-1 + \dfrac{\sqrt{3}}{3}}{1 - -1 \times \dfrac{\sqrt{3}}{3}}\\\\ &=\dfrac{\ \dfrac{-3 + \sqrt{3}}{3}\ }{\ \dfrac{3+\sqrt{3}}{3}}\\\\&=\dfrac{-3 + \sqrt{3}}{3} \times \dfrac{3}{3+\sqrt{3}}\\\\&=\dfrac{-3+\sqrt{3}}{3+\sqrt{3}}\end{align}||On doit rationaliser la fraction en multipliant par le conjugué du dénominateur.||\begin{align}\dfrac{-3+\sqrt{3}}{3+\sqrt{3}}&=\dfrac{\left(-3 + \sqrt{3}\right)}{\left(3+\sqrt{3}\right)} \color{#ec0000}{\times {\dfrac{\left(3 - \sqrt{3}\right)}{\left(3 - \sqrt{3}\right)}}}\\\\ &=\dfrac{-9+3\sqrt{3}+3\sqrt{3}-3}{9-3\sqrt{3}+3\sqrt{3}-3}\\\\&=\dfrac{-12 + 6\sqrt{3}}{6}\\\\&=-2+\sqrt{3}\end{align}||
Réponse : La valeur exacte de |\tan\left(\dfrac{23\pi}{12}\right)| est |-2+\sqrt{3}.|