Matières
Niveaux
Chaque opération mathématique possède son inverse. En utilisant l'inverse ou la réciproque d'une fonction, il est possible de résoudre presque tous les types d'équations. Dans le cas de la notation logarithmique, elle est la réciproque de la notation exponentielle. Ainsi, lorsque la variable que l'on cherche à isoler se situe à la position des exposants, on peut utiliser les logarithmes.
L'application de la définition et des lois des logarithmes sera mise à profit en mathématiques financières pour la résolution de mises en situation impliquant des intérêts composés.
Aussi, cette fiche est primordiale pour l'étude des fonctions exponentielle et logarithmique.
Un logarithme est un exposant dont il faut affecter un autre nombre appelé base du logarithme pour obtenir un nombre donné (argument).
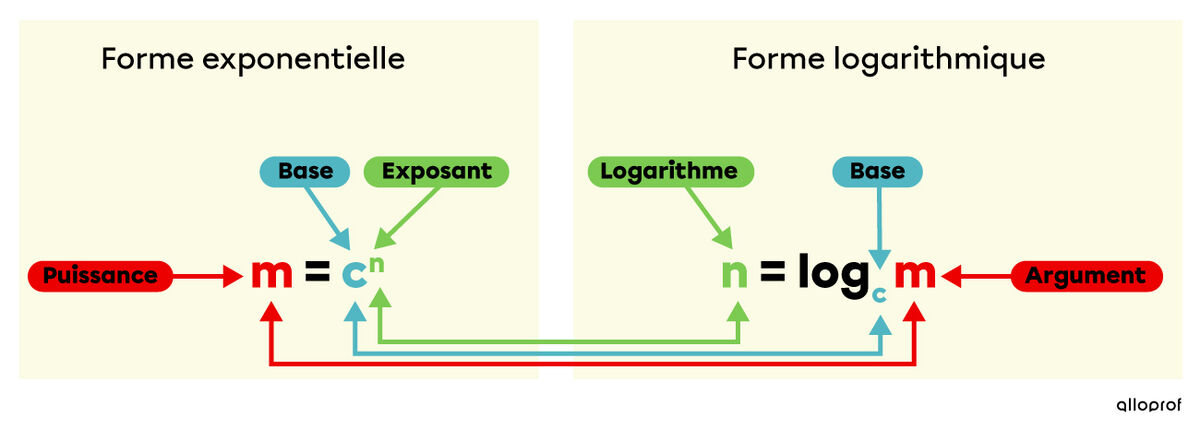
On se pose la question «quel exposant faut-il attribuer à la base |c| pour obtenir le nombre |m|?». C'est ce à quoi correspond le logarithme.
Remarques : Il faut maitriser le vocabulaire lorsqu'on est sous la forme exponentielle ou la forme logarithmique.
À certaines occasions, on appelle l'argument du logarithme : la puissance.
Par définition du logarithme, on obtient que |c^{\log_c m} = m|.
Il existe plusieurs bases. Voici les deux plus fréquentes bases utilisées :
Par convention, lorsque la base du logarithme est 10, on ne l'écrit pas : |\log_{10}m=\log m.|
On utilise très fréquemment ce qu'on appelle le logarithme naturel qui est en fait un logarithme dont la base est le nombre |e=2{,}718\,281\,828\dots| Ce nombre est ce qu'on appelle un nombre irrationnel, c'est-à-dire qu'il a un développement infini et non périodique.
Lorsque la base du logarithme est |e,| on écrit |\ln | plutôt que |\log_e.|
Finalement, peu importe la base utilisée, |m \neq 0| étant donné qu'il n'existe aucune valeur réelle telle que |c^n=0|.
La base |c| du logarithme doit remplir deux conditions :
|c>0|
|c \neq 1|
L'argument |m| du logarithme doit être supérieur à 0.
Exemple 1
||\begin{alignat}{1} \log_\color{blue}{2}(\color{red}{8}) &\Rightarrow \small\text{Quel}&&\small\color{green}{\text{ exposant}}\small \text{ doit-on donner à la}\color{blue}{\text{ base}}\small \text{ pour obtenir } \color{red}{\text{l'argument}}\small \text{?}\\
&\Rightarrow\quad \color{blue}{2}^\color{green}{?} &&= \color{red}{8}\\
&\Rightarrow\quad \color{blue}{2}^\color{green}{?} &&= \color{red}{2^3} \\
&\Rightarrow\quad\ \color{green}{?} &&= 3 \end{alignat}||
Ainsi, la valeur du |\log_\color{blue}{2}(\color{red}{8})=\color{green}{3}.|
Exemple 2
||\begin{alignat}{1} \log_\color{blue}{3}(\color{red}{243}) &\Rightarrow \small\text{Quel}&&\small\color{green}{\text{ exposant}}\small \text{ doit-on donner à la}\color{blue}{\text{ base}}\small \text{ pour obtenir } \color{red}{\text{l'argument}}\small \text{?}\\
&\Rightarrow\quad \color{blue}{3}^\color{green}{?} &&= \color{red}{243}\\
&\Rightarrow\quad \color{blue}{3}^\color{green}{?} &&= \color{red}{3^5} \\
&\Rightarrow\quad\ \color{green}{?} &&= 5 \end{alignat}||
Ainsi, la valeur du |\log_\color{blue}{3}(\color{red}{243})=\color{green}{5}.|
Exemple 3
||\begin{alignat}{1} \log_\color{blue}{\frac{1}{4}}(\color{red}{64}) &\Rightarrow \small\text{Quel}&&\!\!\!\!\!\!\!\!\!\!\!\small\color{green}{\text{ exposant}}\small \text{ doit-on donner à la}\color{blue}{\text{ base}}\small \text{ pour obtenir } \color{red}{\text{l'argument}}\small \text{?}\\
&\Rightarrow\quad \color{blue}{\left(\dfrac{1}{4}\right)}^{\!\color{green}{?}} &&= \color{red}{64}\\
&\Rightarrow\quad \color{blue}{\left(\dfrac{1}{4}\right)}^{\!\color{green}{?}} &&= \color{red}{4^3} \\
&\Rightarrow\quad \color{blue}{\left(\dfrac{1}{4}\right)}^{\!\color{green}{?}} &&= \left(\dfrac{1}{4}\right)^{\!-3} \\
&\Rightarrow\qquad\quad \color{green}{?} &&= -3 \end{alignat}||
Ainsi, la valeur du |\log_\color{blue}{\frac{1}{4}}(\color{red}{64})=\color{green}{-3}.|
Malheureusement, il n'est pas toujours possible de calculer un logarithme sans faire usage de la calculatrice. Les lois des logarithmes permettent de faire beaucoup de calculs.
Pour valider ta compréhension à propos des lois des logarithmes et des exposants de façon interactive, consulte la MiniRécup suivante :
