Matières
Niveaux
En statistique, l'utilisation des diagrammes est très utile afin de bien observer la répartition des données.
Le diagramme à bandes permet de décrire les effectifs observés. Il est utilisé pour présenter des données qualitatives ou des données quantitatives discrètes. Les caractéristiques du diagramme à bandes sont les suivantes.
Chaque bande est associée à une valeur ou à une modalité.
La longueur d’une bande est proportionnelle à son effectif.
La distance entre chacune des bandes doit être la même et la première bande ne doit pas être collée sur l'axe qui lui est parallèle.
La largeur des bandes doit être uniforme.
Le diagramme doit avoir un titre et les axes doivent être identifiés selon ce qu'ils représentent.
Les bandes peuvent être disposées à la verticale ou à l’horizontale.
Voici une table de valeurs et un diagramme à bandes horizontales qui présentent le nombre de points accumulés au cours de la saison de soccer de quatre équipes différentes.
|
Équipe de soccer |
A |
B |
C |
D |
|---|---|---|---|---|
|
Nombre de points accumulés |
|35| |
|22| |
|27| |
|43| |
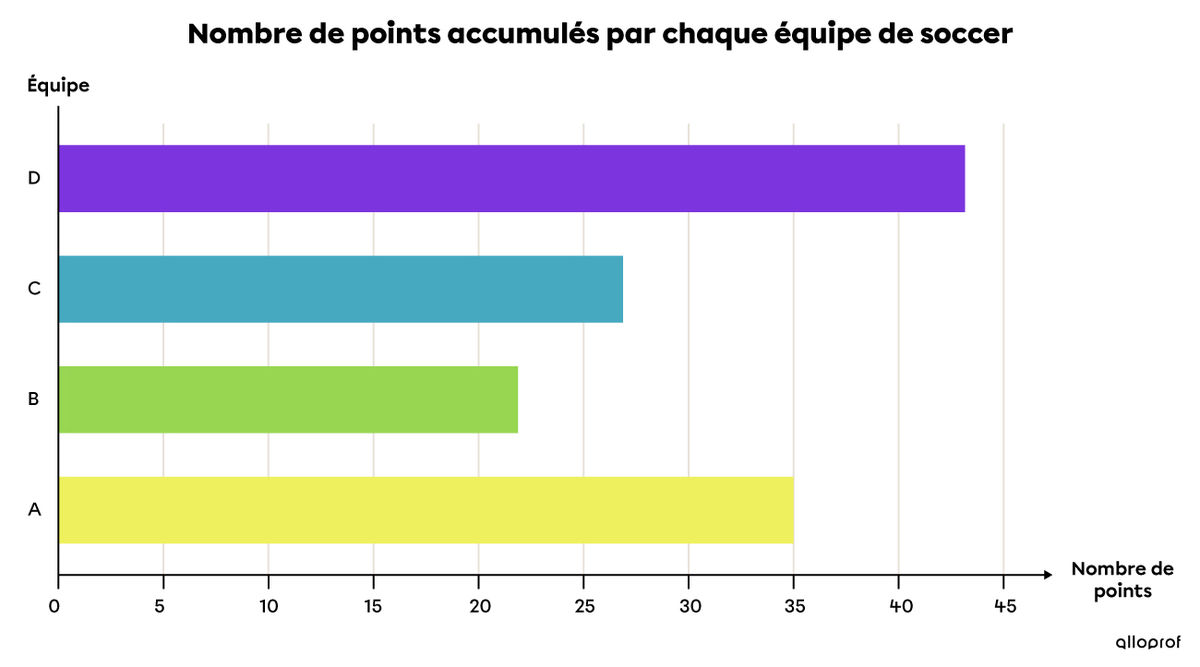
Pour ce qui est du diagramme à bandes verticales, il faut respecter les mêmes contraintes. Ainsi, seule l'orientation des bandes est différente.
Une enquête a été menée pour déterminer l’animal de compagnie préféré des résidents d'une municipalité. Voici la table de valeurs et le diagramme à bandes verticales qui présentent les résultats.
|
Animal de compagnie préféré |
Oiseau |
Chat |
Chien |
Poisson |
|---|---|---|---|---|
|
Nombre de personnes |
|10| |
|20| |
|25| |
|30| |
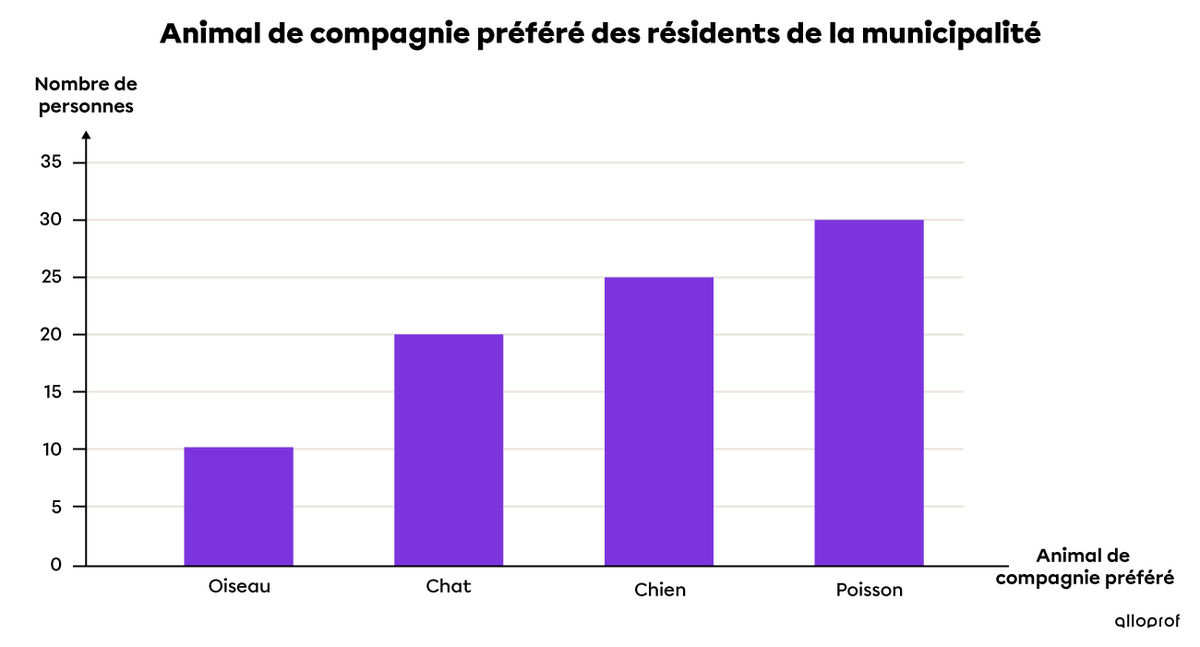
Le diagramme à ligne brisée permet de décrire des données quantitatives discrètes et quantitatives continues qui évoluent dans le temps. Les caractéristiques du diagramme à ligne brisée sont les suivantes.
Chaque point est placé selon l’axe des |x| et l’axe des |y.|
Généralement, ce diagramme fait référence à une situation qui évolue dans le temps (années, mois, jours, etc.).
Il faut commencer à relier les points à partir du premier d'entre eux pour ensuite tracer des lignes droites entre chaque points consécutifs.
Le diagramme doit avoir un titre et les axes doivent être identifiés selon ce qu’ils représentent.
Cet hiver, Charles, un élève de première secondaire, a éprouvé de graves problèmes de santé. Voici la fluctuation de sa masse dans une table de valeurs ainsi que dans un diagramme à ligne brisée.
|
Mois |
Nov. |
Déc. |
Janv. |
Fév. |
Mars |
Avril |
|---|---|---|---|---|---|---|
|
Masse (kg) |
|44| |
|42| |
|43| |
|46| |
|44| |
|41| |
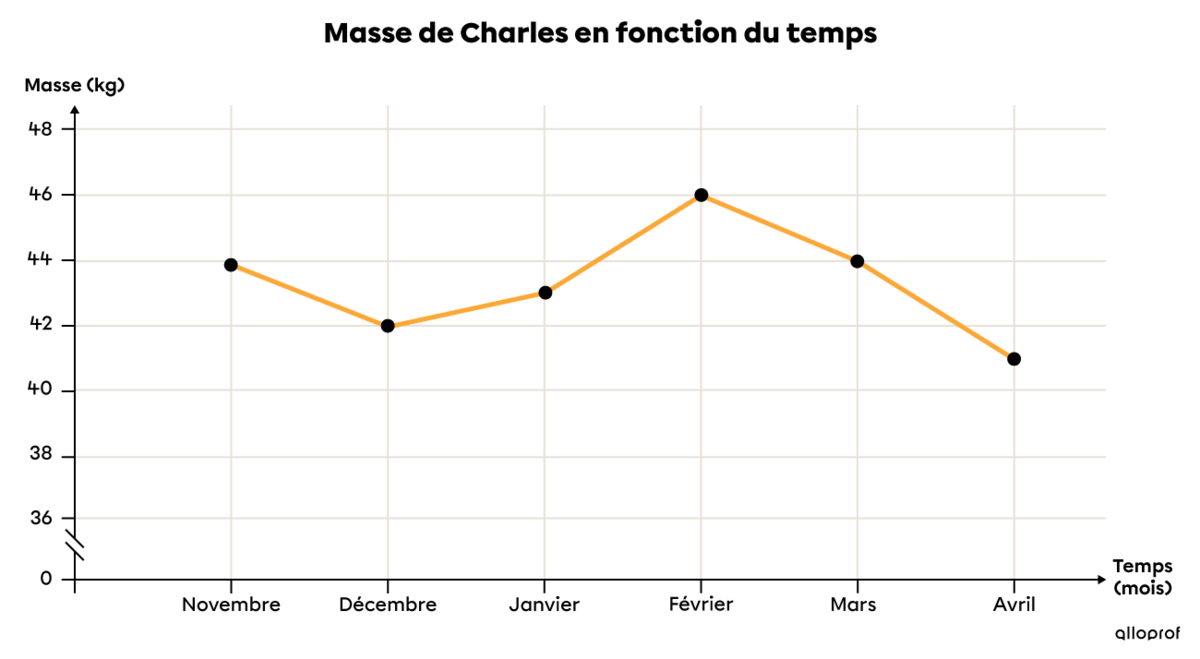
On peut également représenter des effectifs sous la forme de pictogrammes. Contrairement aux autres diagrammes, ceux-ci sont composés de dessins qui sont associés à des quantités.
Par une belle soirée d’été, Marie et Simon comptent les étoiles qu’ils peuvent apercevoir. Marie en compte |65,| alors que Simon en compte |70.| Ainsi, on peut représenter cette situation de la manière suivante.
|
Nombre d’étoiles observées |
 |
|---|---|
|
Nombre d’étoiles observées |
 |
Légende : un pictogramme en forme d’étoile représente |10| étoiles.
Pour interpréter des pictogrammes, il faut d’abord lire et comprendre la légende. Dans ce cas, on sait qu’un pictogramme en forme d’étoile représente |10| étoiles. Également, on peut déduire qu’un pictogramme en forme de demi-étoile représente la moitié de |10| étoiles, soit |5| étoiles.
Dans l’exemple précédent, on peut compter |6{,}5| pictogrammes en forme d’étoiles ce qui correspond aux |65| étoiles observées par Marie.
Le diagramme circulaire permet d'illustrer un tout partagé en parties. On l'utilise pour représenter des données qualitatives. Les caractéristiques du diagramme circulaire sont les suivantes.
Chaque secteur du cercle est en lien avec une modalité généralement présentée avec un pourcentage.
L’angle au centre d’un secteur circulaire représente la proportion d’une catégorie par rapport au tout |(360^\circ).|
Il doit y avoir un titre et une légende qui associe le contenu des secteurs à une modalité.
On a interrogé |160| élèves d'une école secondaire au sujet de leur saison préférée. Voici le tableau de distribution des résultats obtenus.
|
Modalité |
Effectif |
Fréquence relative |
Angle au centre |
|---|---|---|---|
|
Hiver |
|48| |
|30| |
|108| |
|
Automne |
|24| |
|15| |
|54| |
|
Printemps |
|16| |
|10| |
|36| |
|
Été |
|72| |
|45| |
|162| |
|
Total |
|160| |
|100| |
|360| |
On calcule la fréquence relative d’une donnée à l’aide de la proportion suivante.||\dfrac{\text{Fréquence relative}}{100}=\dfrac{\text{Effectif}}{\text{Effectif total}}||On calcule l’angle au centre en utilisant l’une des 2 proportions suivantes.
||\dfrac{\text{Angle au centre d'un secteur}}{360^\circ}=\dfrac{\text{Effectif}}{\text{Effectif total}}||
||\dfrac{\text{Angle au centre d'un secteur}}{360^\circ}=\dfrac{\text{Fréquence relative}}{100}||
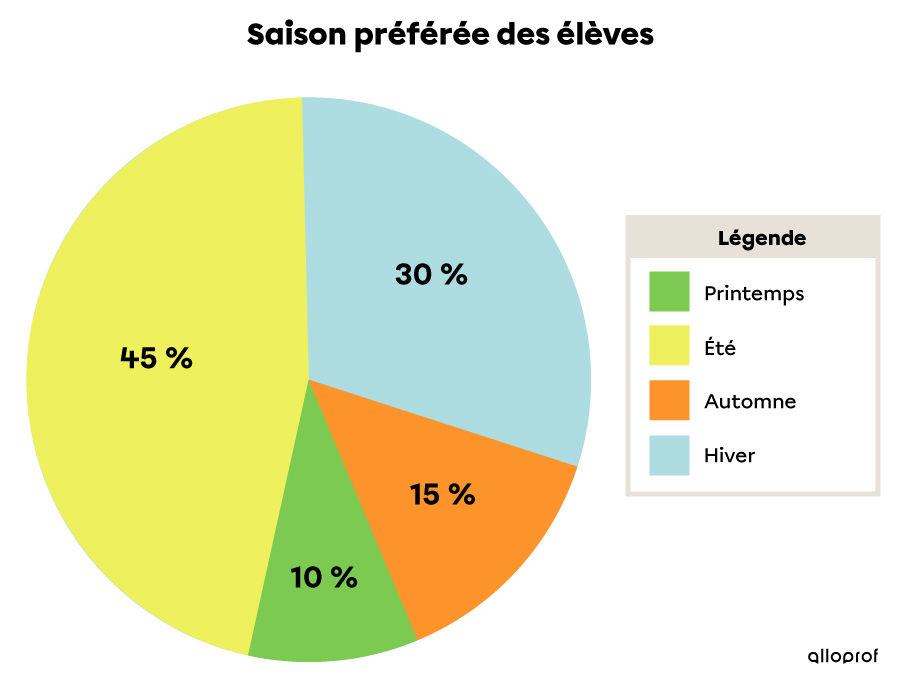
Puisque le diagramme circulaire est construit à l'aide d'un cercle, on peut utiliser ses caractéristiques afin de déduire des quantités manquantes.
Voici le tableau de distribution incomplet d'un diagramme circulaire.
|
Modalité |
Effectif |
Fréquence relative |
Angle au centre |
|---|---|---|---|
|
Hiver |
|48| |
|30| |
|108| |
|
Automne |
|
|15| |
|
|
Printemps |
|16| |
|
|36| |
|
Été |
|
|45| |
|
|
Total |
|
|100| |
|360| |
Pour trouver la quantité à inscrire dans la case verte, on peut utiliser la proportion suivante.||\begin{align}\dfrac{30}{15}&=\dfrac{108}{\color{#3a9a38}{\text{case verte}}}\\\\\color{#3a9a38}{\text{case verte}}&=15\times108\div30\\&=54\end{align}||
L’histogramme permet de décrire les effectifs observés. Il est utilisé pour présenter des données quantitatives discrètes et quantitatives continues groupées en classes. Les caractéristiques de l'histogramme sont les suivantes.
Les bandes sont collées les unes contre les autres.
Sur l’axe vertical, on indique la fréquence de chaque valeur.
Sur l’axe horizontal, on indique les classes.
Dans l'histogramme suivant, on représente le nombre de personnes qui ont assisté à un concert en fonction du groupe d'âge auquel ces personnes appartiennent.
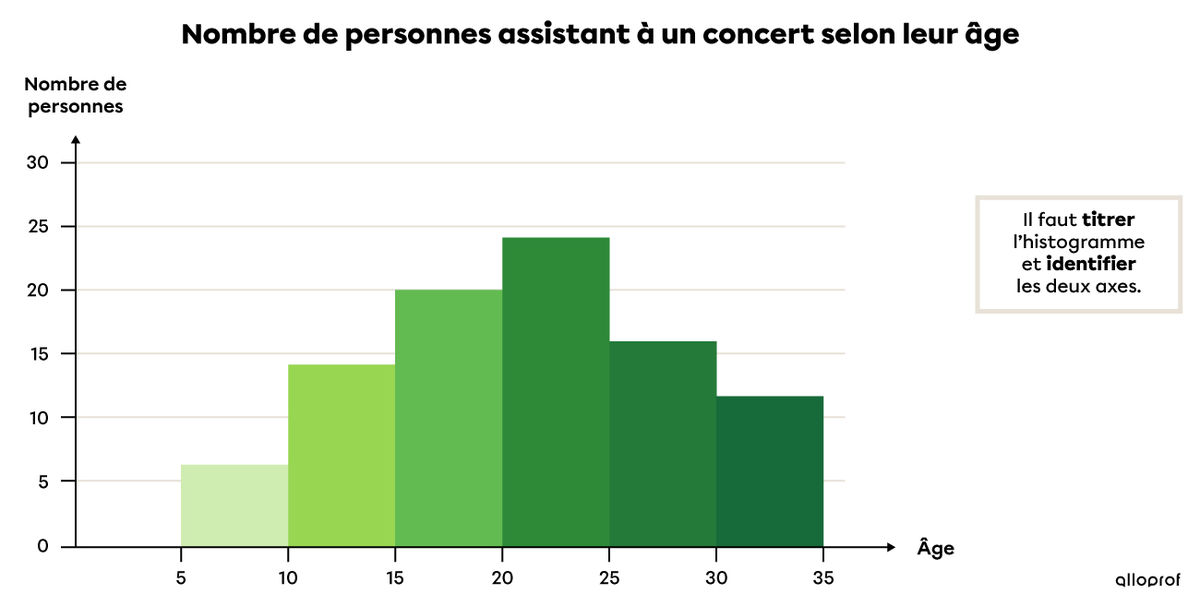
À partir de cet histogramme, on peut en déduire le tableau de distribution suivant.
|
Tranche d'âge |
Nombre de personnes |
|---|---|
|
|[0,5[| |
|0| |
|
|[5,10[| |
|7| |
|
|[10,15[| |
|14| |
|
|[15,20[| |
|20| |
|
|[20,25[| |
|24| |
|
|[25,30[| |
|16| |
|
|[30,35[| |
|12| |
Le diagramme à tige et à feuilles permet de décrire les effectifs observés. Il est utilisé pour présenter des données quantitatives discrètes. Les caractéristiques du diagramme à tige et à feuilles sont les suivantes.
Chaque ligne est associée à un intervalle de données.
Chaque donnée est décomposée en deux parties (la tige et la feuille) se trouvant sur une même ligne.
Pour lire un tel diagramme, il faut toujours associer un chiffre de la tige (colonne du centre) avec un chiffre d'une feuille (colonne de gauche ou de droite). Les feuilles avec les plus petits chiffres sont plus près de la tige, alors que celles avec les plus grands chiffres sont situées plus loin de la tige.
Voici un diagramme à tige et à feuilles qui contient l’âge de 37 personnes.
| Femmes | Hommes | |
|---|---|---|
|
|6\!-\!5\!-\!2\!-\!2| |
|0| |
|2\!-\!3\!-\!4\!-\!5| |
|
|4\!-\!3\!-\!3\!-\!1| |
|1| |
|0\!-\!0\!-\!1\!-\!6\!-\!8| |
|
|9\!-\!9\!-\!8\!-\!4\!-\!3| |
|2| |
|2\!-\!2\!-\!5\!-\!7\!-\!8| |
|
|9\!-\!8\!-\!7\!-\!6\!-\!5| |
|3| |
|1\!-\!8\!-\!8\!-\!8\!-\!9| |
Dans le cas présent, la colonne du milieu indique le 1er chiffre, soit celui à la position des dizaines, de l’âge des personnes et les chiffres des colonnes de gauche (femmes) et de droite (hommes) sont associés au chiffre à la position des unités de chaque âge.
Par exemple, il y a 5 hommes de cet échantillon qui sont dans la vingtaine (chiffre |2| dans la colonne du centre). Plus précisément, ils sont âgés de |22,| |22,| |25,| |27| et |28| ans.
Pour la même tranche d'âge, les 5 femmes de cet échantillon sont âgées de |23,| |24,| |28,| |29| et |29| ans.
À l'inverse, on pourrait décider de construire un diagramme à tige et à feuilles à partir d'une distribution composée d’un seul groupe.
Lors de son retour d'un voyage de pêche, Gitane a noté la longueur de chacune de ses prises, en millimètres, et en voici la liste.
|203,| |204,| |206,| |209,| |210,| |212,| |212,| |218,| |226,| |234,| |239,| |240,| |242,| |242,| |242,| |245,| |249,| |250,| |251,| |252,| |257,| |258,| |260,| |262,| |263,| |264|
Pour alléger l'énumération, elle utilise un diagramme à tige et à feuilles. Dans ce cas, la tige est composée des chiffres de la position des dizaines et des centaines, alors que les feuilles sont composées des chiffres des unités de chaque donnée. Elle obtient le tableau suivant.
|
Tige |
Feuilles |
|---|---|
|
|20| |
|3\!-\!4\!-\!6\!-\!9| |
|
|21| |
|0\!-\!2\!-\!2\!-\!8| |
|
|22| |
|6| |
|
|23| |
|4\!-\!9| |
|
|24| |
|0\!-\!2\!-\!2\!-\!2\!-\!5\!-\!9| |
|
|25| |
|0\!-\!1\!-\!2\!-\!7\!-\!8| |
|
|26| |
|0\!-\!2\!-\!3\!-\!4| |