Matières
Niveaux
Lorsque le nuage de points d’une distribution de données à 2 variables montre une corrélation linéaire, la distribution peut être modélisée par une droite de régression.
La droite de régression est la droite qu’on peut tracer dans le nuage de points qui représente le mieux la distribution à deux caractères étudiée. Il existe plusieurs manières de trouver l’équation de cette droite de régression. Outre l'utilisation des calculatrices graphiques et de certains logiciels, on peut calculer manuellement l'équation de la droite de régression.
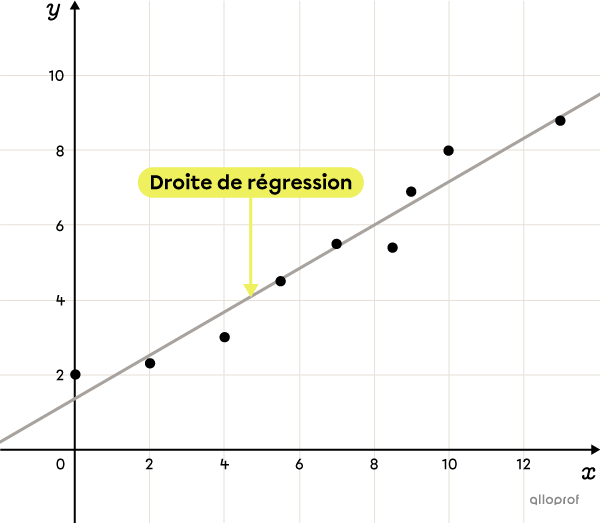
Une droite de régression sert à prédire la valeur d’une variable à partir de la valeur de l’autre variable par extrapolation ou interpolation.
Il existe plusieurs méthodes pour trouver l’équation d’une droite de régression.
Comme son nom l’indique, il suffit de tracer une droite qui passe au travers du nuage de points de sorte qu’il y ait environ autant de points de chaque côté de la droite et que la pente de la droite s’ajuste le mieux possible à l’orientation du nuage de points.
Par la suite, lorsque la droite est tracée, on peut trouver sa règle à l’aide de 2 points sur celle-ci.
Les graphiques ci-dessous montrent le même nuage de points. Dans le premier, on a tracé 3 droites |(y_1,| |y_2| et |y_3)| qui ne sont pas de bonnes droites de régression, alors que les droites de la 2e figure |(y_4| et |y_5)| peuvent toutes les 2 être considérées comme des droites de régression valables.
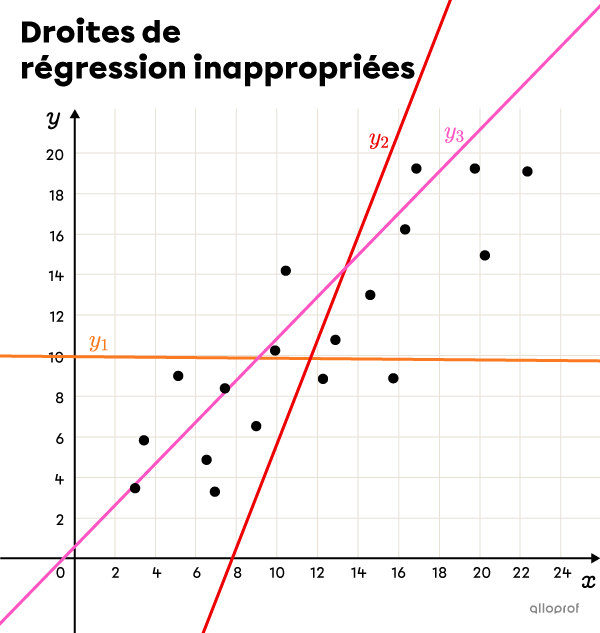
La droite |y_1| n’est pas une bonne droite de régression, car elle est presque constante, alors que le nuage de points présente plutôt une corrélation positive (croissance).
La droite |y_2| n’est pas une bonne droite de régression non plus, car sa pente est beaucoup plus prononcée que le nuage de points.
La droite |y_3| a une pente qui ressemble à celle du nuage de points, mais elle n’a pas le même nombre de points des 2 côtés.
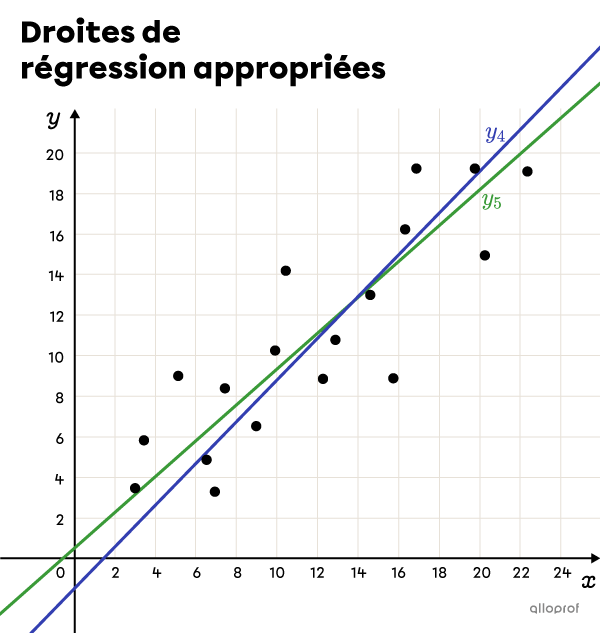
Les droites |y_4| et |y_5| sont 2 droites qui représentent beaucoup mieux la tendance du nuage de points et qui comptent le même nombre de points de chaque côté. Il est possible d’utiliser l’une ou l’autre de ces droites pour faire des prédictions.
Bien que la méthode à main levée soit acceptable dans la plupart des situations, c’est la méthode la moins précise. Comme on peut le voir dans l’exemple précédent, 2 droites semblent convenir pour le même nuage de points, même si elles ont des pentes légèrement différentes. Pour plus de précisions, il vaut mieux favoriser une autre méthode comme la droite de Mayer ou la droite médiane-médiane.
Les étapes à suivre pour prédire une donnée à partir d’un nuage de points en utilisant la méthode graphique sont les suivantes.
Placer les points dans un plan cartésien.
Tracer une droite de régression.
Déterminer 2 points situés sur la droite de régression.
Trouver la règle de la droite à l’aide de ces 2 points.
Prédire une valeur à l’aide de la règle.
À la suite d’une enquête réalisée auprès de |16| familles québécoises, on s'est intéressé aux dépenses totales liées aux sports et aux loisirs en fonction de leur revenu familial. La table de valeurs ci-dessous présente les données recueillies.
| Revenu familial ($/année) |
|125\ 000| | |65\ 000| | |35\ 000| | |145\ 000| | |130\ 000| | |80\ 000| | |50\ 000| | |40\ 000| |
|---|---|---|---|---|---|---|---|---|
| Dépenses liées aux sports et aux loisirs ($/année) |
|10\ 000| | |8\ 000| | |1\ 000| | |9\ 000| | |8\ 000| | |6\ 000| | |4\ 000| | |2\ 000| |
| Revenu familial ($/année) |
|90\ 000| | |20\ 000| | |75\ 000| | |105\ 000| | |100\ 000| | |140\ 000| | |150\ 000| | |65\ 000| |
| Dépenses liées aux sports et aux loisirs ($/année) |
|10\ 000| | |500| | |4\ 000| | |6\ 000| | |8\ 000| | |13\ 000| | |5\ 000| | |5\ 000| |
a) Une famille a un revenu familial annuel de |250\ 000\ \$.| Si cette famille suit la même tendance que les autres familles québécoises interrogées, à quel montant son budget consacré aux sports et aux loisirs s'élève-t-il?
b) Une famille dépense en moyenne |7\ 500\ \$| par année pour les sports et les loisirs. À combien son revenu familial annuel s’élève-t-il si elle suit les habitudes d’une famille québécoise typique?
Placer les points dans un plan cartésien
On place le revenu familial annuel sur l’axe des |x| et les dépenses liées aux sports et aux loisirs sur l’axe des |y.|
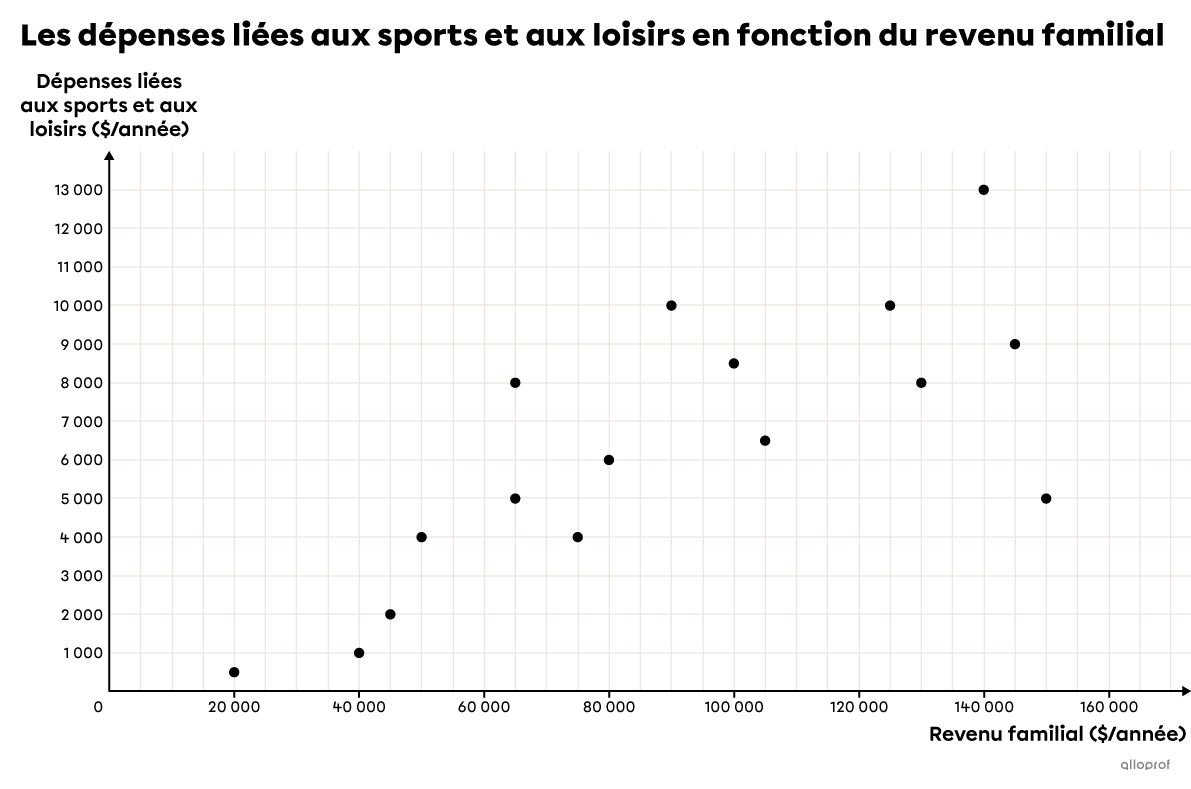
Tracer une droite de régression
Comme il y a |16| points dans le nuage de points, on s’assure d’en placer |8| de part et d’autre de la droite. On s’assure également d’avoir une droite dont la pente s’ajuste bien au nuage de points.
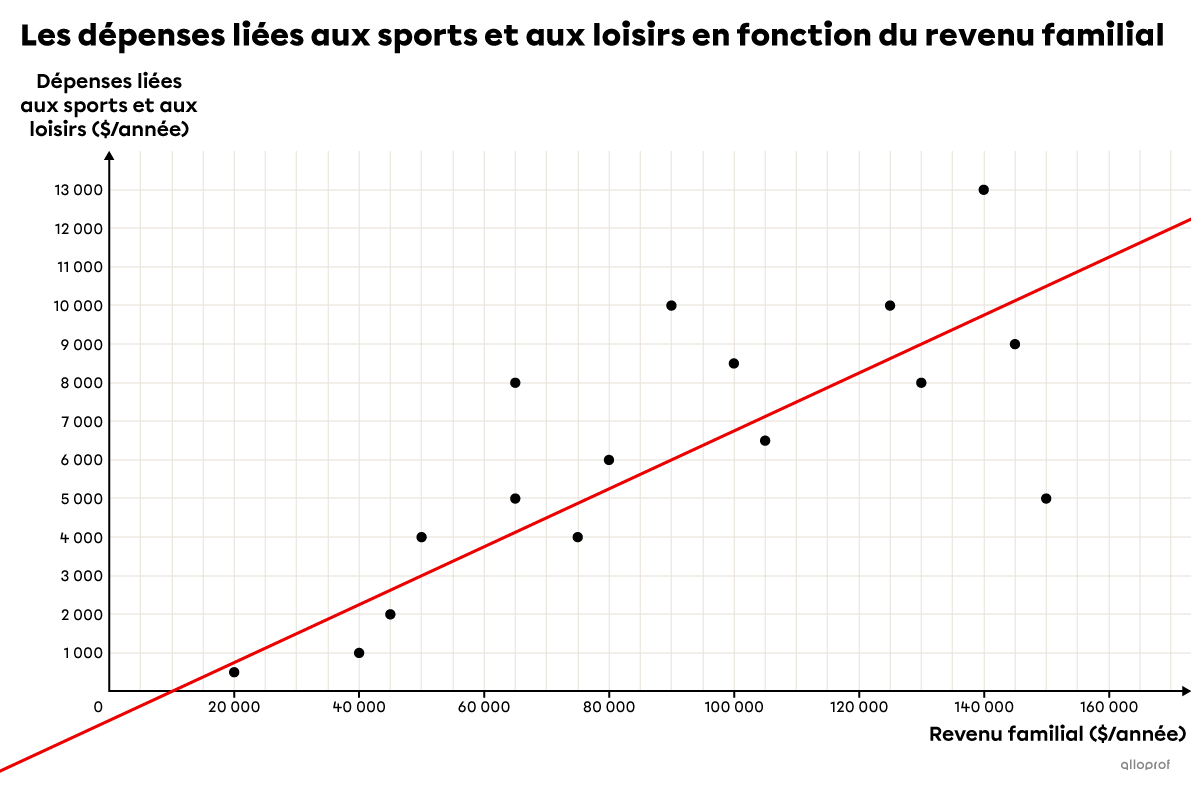
Remarque : La droite aurait pu être tracée un peu plus haut ou un peu plus bas. Si c'est le cas, alors la règle et les prédictions peuvent varier légèrement en conséquence.
Déterminer 2 points situés sur la droite de régression
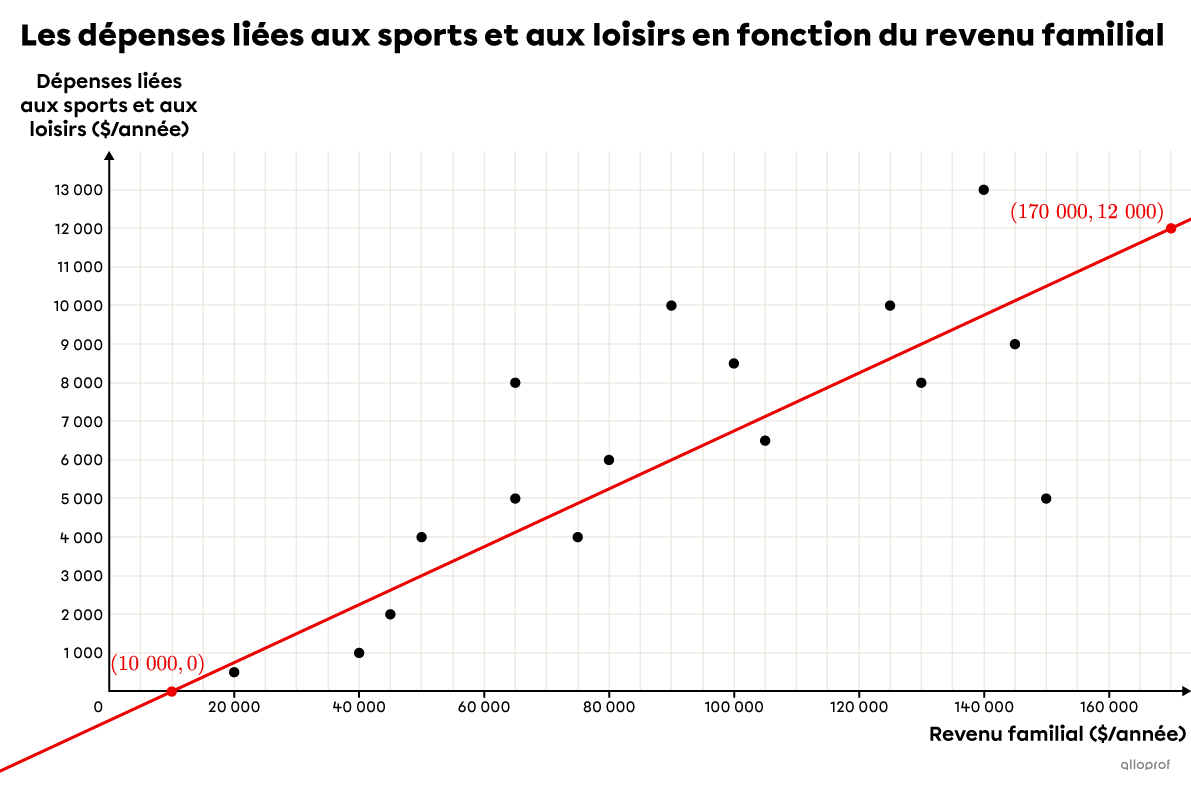
On choisit le point |(10\ 000, 0)| et le point |(170\ 000, 12\ 000).|
Trouver la règle de la droite à l’aide de ces 2 points
Comme il s’agit d’une droite, la règle sera de la forme |y=ax+b.|
On commence par calculer la pente |(a).| ||\begin{align}a&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{12\ 000-0}{170\ 000-10\ 000}\\&=\dfrac{12\ 000}{160\ 000}\\&=\dfrac{3}{40}\\ &=0{,}075\end{align}||Ensuite, on remplace |a| par |0{,}075| et les variables |x| et |y| par les coordonnées d’un des 2 points, puis on isole |b.| ||\begin{align}y&=ax+b\\ y&=0{,}075x+b\\0&=0{,}075(10\ 000)+b\\0&=750+b\\-750&=b \end{align}||Ainsi, la règle de la droite de régression tracée à main levée est |y=0{,}075x-750.|
Prédire une valeur à l’aide de la règle
a) Une famille a un revenu familial annuel de |\boldsymbol{250\ 000\ \$.}| Si cette famille suit la même tendance que les autres familles québécoises interrogées, à quel montant son budget consacré aux sports et aux loisirs s'élève-t-il?
Il s’agit d’une prédiction par extrapolation, car le revenu familial en question |(250\ 000\ \$)| est en dehors de l’intervalle des revenus familiaux étudiés, qui étaient tous situés entre |20\ 000| et |150\ 000\ \$.|
On remplace la variable |x| par |250\ 000\ \$| dans la règle de la droite de régression et on complète le calcul. ||\begin{align}y&=0{,}075x-750\\y&=0{,}075(250\ 000)-750\\y&=18\ 750-750\\y&=18\ 000\ \$ \end{align}||
Réponse : Si une famille ayant un revenu annuel de |250\ 000\ \$| suit la même tendance que les autres familles québécoises interrogées, elle devrait consacrer |18\ 000\ \$| aux sports et aux loisirs.
b) Une famille dépense en moyenne |\boldsymbol{7\ 500\ \$}| par année pour les sports et les loisirs. À combien son revenu familial annuel s’élève-t-il si elle suit les habitudes d’une famille québécoise typique?
Il s’agit d’une prédiction par interpolation, car le budget annuel consacré aux loisirs et aux sports |(7\ 500\ \$)| est à l’intérieur de l’intervalle étudié |(500| à |13\ 000\ \$).| On peut donc faire une estimation du revenu annuel de cette famille à l’aide de la droite de régression.
On remplace la variable |y| par |7\ 500\ \$| et on isole |x.| ||\begin{align} y &= 0{,}075x-750 \\ 7\ 500 &= 0{,}075x-750 \\ 7\ 500\boldsymbol{\color{#ec0000}{+750}} &= 0{,}075x-750\boldsymbol{\color{#ec0000}{+750}} \\ \color{#ec0000}{\dfrac{\color{black}{8\ 250}}{\boldsymbol{0{,}075}}} &= \color{#ec0000}{\dfrac{\color{black}{0{,}075x}}{\boldsymbol{0{,}075}}} \\ 110\ 000\ \$ &= x \end{align}||
Réponse : Si une famille dépense en moyenne |7\ 500\ \$| par année pour les sports et les loisirs, on peut s’attendre à ce que son revenu familial annuel soit d’environ |110\ 000\ \$.|
Dans le graphique, on peut voir que la droite de régression qu’on a tracée passe bel et bien par le point |(110\ 000, 7\ 500).|
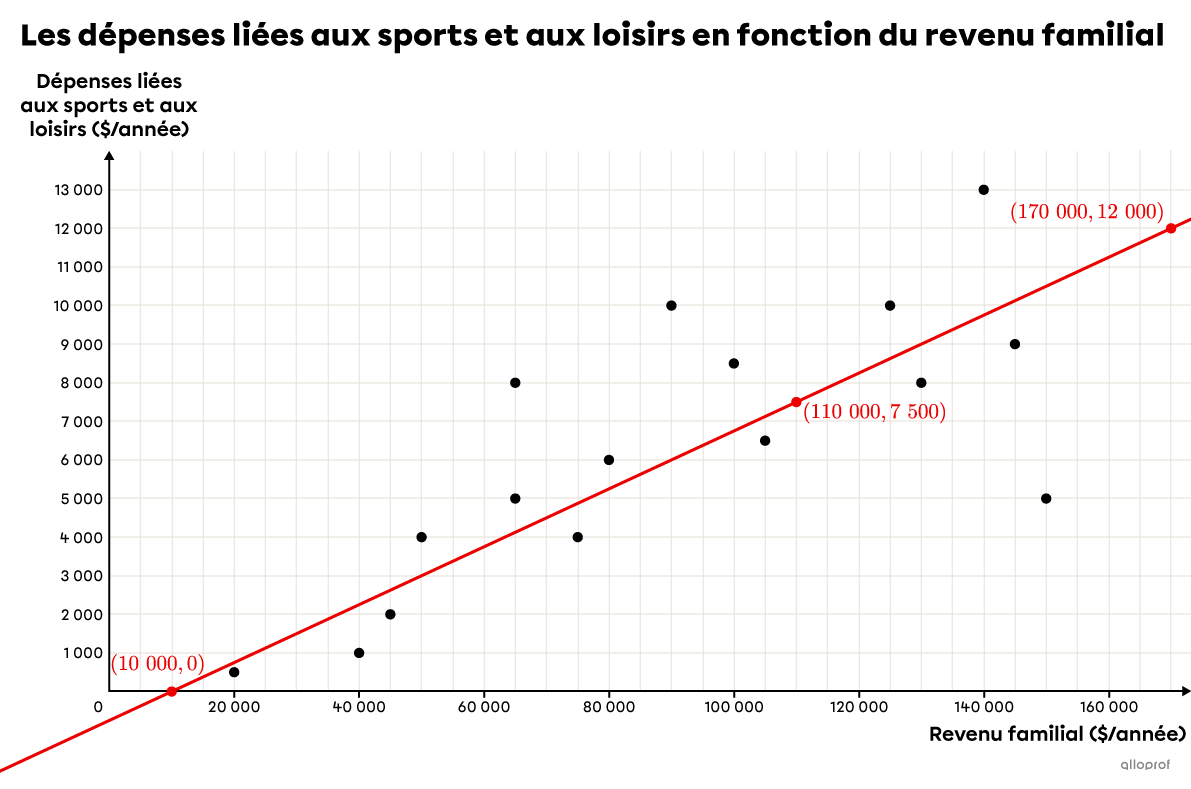
Remarque : Le même problème a été résolu dans les fiches portant sur la droite médiane-médiane et sur la droite de Mayer. Chaque fois, on obtient des résultats comparables.
Les tableurs sont des logiciels qui permettent de faire des tableaux et des graphiques. Ils sont programmés pour calculer des coefficients de corrélation et pour calculer l’équation de la droite ou de la courbe qui modélise le mieux un nuage de points donné.
L’utilisation des tableurs est donc la méthode la plus rapide, la plus polyvalente et la plus efficace pour trouver la règle d’une droite de régression et pour prédire des résultats par la suite.
À la suite d’une enquête réalisée auprès de |16| familles québécoises, on s'est intéressé aux dépenses totales liées aux sports et aux loisirs en fonction de leur revenu familial. La table de valeurs ci-dessous présente les données recueillies.
| Revenu familial ($/année) |
|125\ 000| | |65\ 000| | |35\ 000| | |145\ 000| | |130\ 000| | |80\ 000| | |50\ 000| | |40\ 000| |
|---|---|---|---|---|---|---|---|---|
| Dépenses liées aux sports et aux loisirs ($/année) |
|10\ 000| | |8\ 000| | |1\ 000| | |9\ 000| | |8\ 000| | |6\ 000| | |4\ 000| | |2\ 000| |
| Revenu familial ($/année) |
|90\ 000| | |20\ 000| | |75\ 000| | |105\ 000| | |100\ 000| | |140\ 000| | |150\ 000| | |65\ 000| |
| Dépenses liées aux sports et aux loisirs ($/année) |
|10\ 000| | |500| | |4\ 000| | |6\ 000| | |8\ 000| | |13\ 000| | |5\ 000| | |5\ 000| |
a) Une famille a un revenu familial annuel de |250\ 000\ \$.| Si cette famille suit la même tendance que les autres familles québécoises interrogées, à quel montant son budget consacré aux sports et aux loisirs s'élève-t-il?
b) Une famille dépense en moyenne |7\ 500\ \$| par année pour les sports et les loisirs. À combien son revenu familial annuel s’élève-t-il si elle suit les habitudes d’une famille québécoise typique?
Transcrire la table de valeur dans le tableur
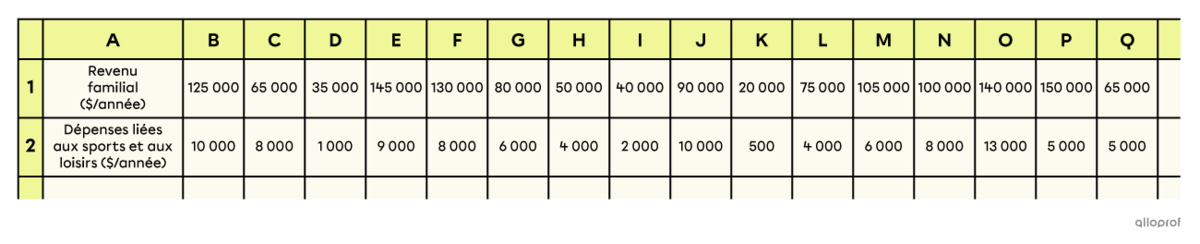
Tracer le nuage de points
En sélectionnant les cases A1 à Q2, on peut demander au logiciel de tracer le nuage de points pour nous en quelques clics. Le résultat devrait ressembler à ceci.
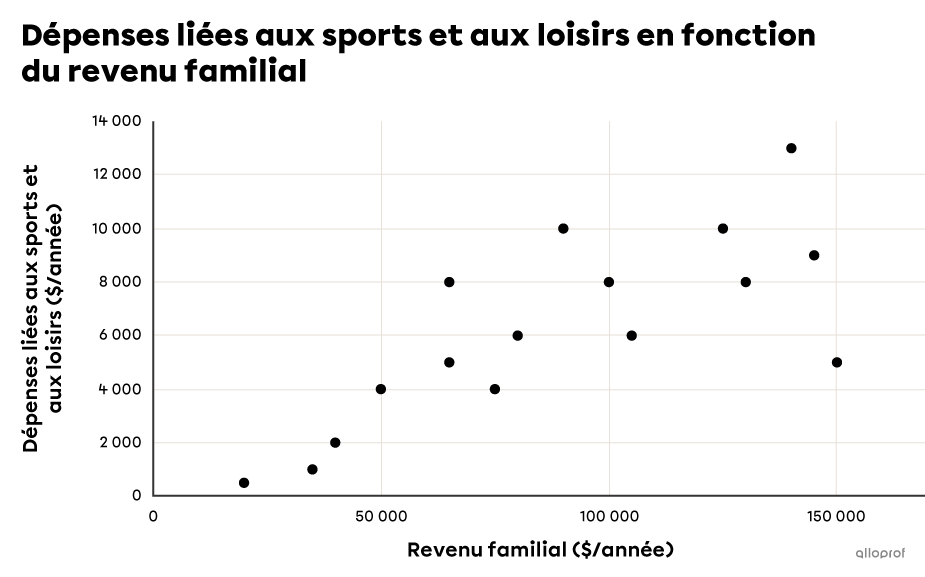
Tracer la droite de régression
En cliquant sur le graphique, on a accès à de nombreuses options. L’une d’entre elles permet de tracer une courbe de tendance. Si on choisit le modèle linéaire, qui est souvent le 1er modèle proposé, on obtient ceci.
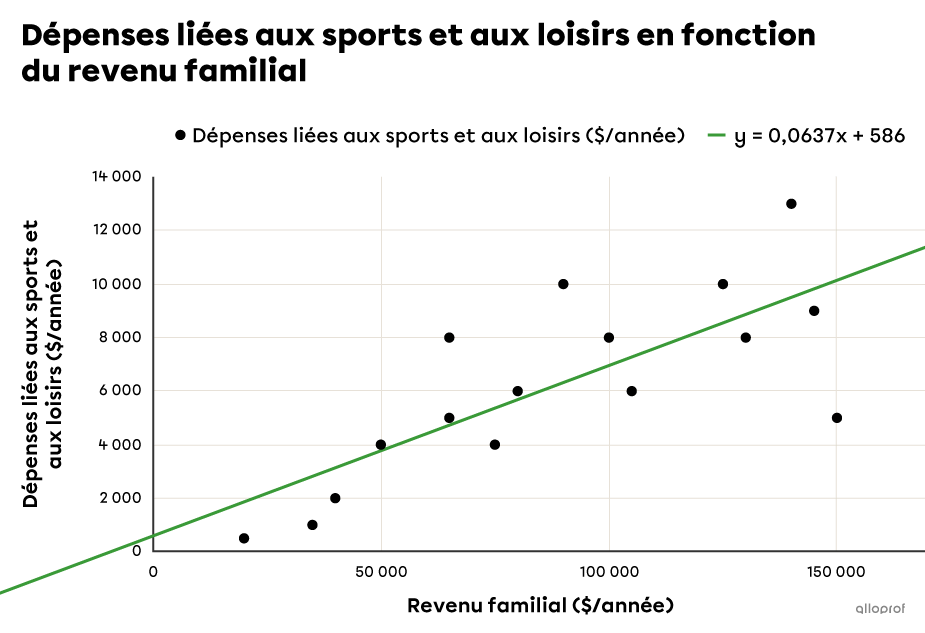
Trouver la règle de la droite à l’aide de ces 2 points
On peut également décider de faire afficher l’équation de la droite ou non. Sur la figure précédente, elle apparait juste en haut du graphique.
Ainsi, la règle de la droite de régression trouvée à l’aide d’un tableur est |y=0{,}063\,7x+586.|
Prédire une valeur à l’aide de la règle
Généralement, les logiciels peuvent faire les calculs qui suivent automatiquement. Il suffit de fournir une valeur de |x| ou de |y| et de demander au logiciel de prédire la valeur de l’autre variable en utilisant la règle qu’il vient de calculer.
a) Une famille a un revenu familial annuel de |\boldsymbol{250\ 000\ \$.}| Si cette famille suit la même tendance que les autres familles québécoises interrogées, à quel montant son budget consacré aux sports et aux loisirs s'élève-t-il?
On remplace la variable |x| par |250\ 000\ \$| dans la règle de la droite de régression et on complète le calcul. ||\begin{align}y&=0{,}063\,7x+586\\y&=0{,}063\,7(250\ 000)+586\\y&=15\ 925+586\\y&=16\ 511\ \$ \end{align}||
Réponse : Si une famille ayant un revenu annuel de |250\ 000\ \$| suit la même tendance que les autres familles québécoises interrogées, elle devrait consacrer environ |16\ 511\ \$| aux sports et aux loisirs.
b) Une famille dépense en moyenne |\boldsymbol{7\ 500\ \$}| par année pour les sports et les loisirs. À combien son revenu familial annuel s’élève-t-il si elle suit les habitudes d’une famille québécoise typique?
On remplace la variable |y| par |7\ 500\ \$| dans la règle de la droite de régression et on isole |x.| ||\begin{align} y &= 0{,}063\,7x+586 \\ 7\ 500 &= 0{,}063\,7x+586 \\ 7\ 500\boldsymbol{\color{#ec0000}{-586}} &= 0{,}063\,7x+586\boldsymbol{\color{#ec0000}{-586}} \\ \color{#ec0000}{\dfrac{\color{black}{6\ 914}}{\boldsymbol{0{,}063\,7}}} &= \color{#ec0000}{\dfrac{\color{black}{0{,}063\,7x}}{\boldsymbol{0{,}063\,7}}} \\ 108\ 540\ \$ &\approx x \end{align}||
Réponse : Si une famille dépense en moyenne |7\ 500\ \$| par année pour les sports et les loisirs, on peut s’attendre à ce que son revenu familial annuel soit d’environ |108\ 540\ \$.|
Remarque : Le même problème a été résolu dans les fiches portant sur la droite médiane-médiane et sur la droite de Mayer. Chaque fois, on obtient des résultats comparables.
Une prédiction faite à partir d’un nuage de points ne peut jamais être parfaitement précise. C’est pourquoi lorsqu’on présente nos prédictions, il est préférable d’utiliser le conditionnel. C’est aussi pourquoi, lors de la correction de ce genre de problèmes, on accepte une marge d’erreur.
Par ailleurs, les différents logiciels ne donnent pas toujours exactement la même règle pour la droite de régression, car ils n’utilisent pas nécessairement le même algorithme pour la calculer. Cependant, la méthode la plus couramment utilisée par les logiciels pour calculer une droite de régression est celle des moindres carrés. Pour savoir comment cela fonctionne concrètement, n’hésite pas à consulter la section suivante portant sur cette méthode algébrique.
Dans la présente fiche, ainsi que dans celles sur les droites de Mayer et médiane-médiane, on montre d’abord comment trouver la règle d’une droite de régression, puis comment utiliser cette règle pour faire des prédictions.
Faire une prédiction, c’est déterminer une nouvelle valeur à partir des données ayant permis d’établir un modèle mathématique. Une prédiction peut être faite par interpolation ou par extrapolation.
L’interpolation consiste à estimer la valeur d’une des 2 variables à l’étude à partir de la valeur de l’autre variable si celle-ci est à l’intérieur de l’intervalle couvert par les données de l’échantillon.
L’extrapolation consiste à prédire la valeur d’une des 2 variables à l’étude à partir de la valeur de l’autre variable si celle-ci est en dehors de l'intervalle couvert par les données de l’échantillon.
En général, on considère que l’interpolation est plus fiable que l’extrapolation. Par exemple, un nuage de points donné peut sembler suivre un modèle linéaire, alors qu’en réalité, il suit plutôt un modèle quadratique, exponentiel ou autre.
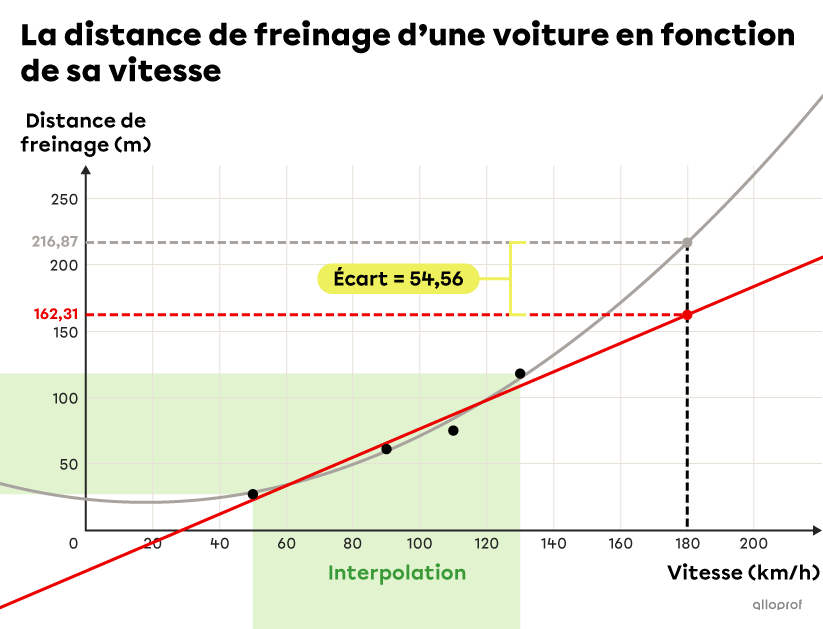
Dans le graphique ci-haut, on présente la distance de freinage d’une voiture en fonction de sa vitesse. Ce phénomène suit un modèle quadratique. On remarque que, sur l’intervalle couvert par le nuage de points, c’est-à-dire de |50| à |130\ \text{km/h},| la droite de régression qui modélise le nuage de points et la courbe réelle sont très proches l’une de l’autre. Ainsi, si on se sert de la droite de régression pour estimer par interpolation la distance de freinage d’une voiture qui roule entre |50| et |130\ \text{km/h},| on obtient une valeur très proche de la valeur réelle.
Par contre, si on se sert de la droite de régression pour prédire par extrapolation la distance de freinage d’une voiture qui roule à |180\ \text{km/h},| soit au-delà de l’intervalle étudié, on obtiendra une valeur éloignée de la valeur réelle.
Autrement dit, ce n’est pas parce qu’un nuage de points montre une tendance linéaire que la même tendance va se poursuivre au-delà du nuage de points.
Le problème sur les dépenses consacrées aux sports et aux loisirs en fonction des revenus familiaux a été fait à l’aide de plusieurs méthodes. Dans le tableau-résumé suivant, il est possible de comparer les différents résultats obtenus.
|
|
Règle obtenue |
Extrapolation |
Interpolation |
|
Méthode graphique |
|y=0{,}075x-750\,\ \ \,| |
|18\ 000\ \$| |
|110\ 000\ \$| |
|
Méthode des moindres carrés |
|y=0{,}063\,7x+586| |
|16\ 511\ \$| |
|108\ 540\ \$| |
|
Méthode de la droite de Mayer |
|y=0{,}07x+6\ \ \ \ \ \ \ | |
|17\ 506\ \$| |
|107\ 057\ \$| |
|
Méthode de la droite médiane-médiane |
|y=0{,}07x-183\ \ \ \,| |
|17\ 317\ \$| |
|109\ 757\ \$| |
On remarque que les règles se ressemblent. Les taux de variation sont très similaires, alors que ce sont les valeurs initiales qui varient le plus. Dans le graphique suivant, on retrouve le nuage de points ainsi que les 4 droites de régression obtenues à l’aide des différentes méthodes.
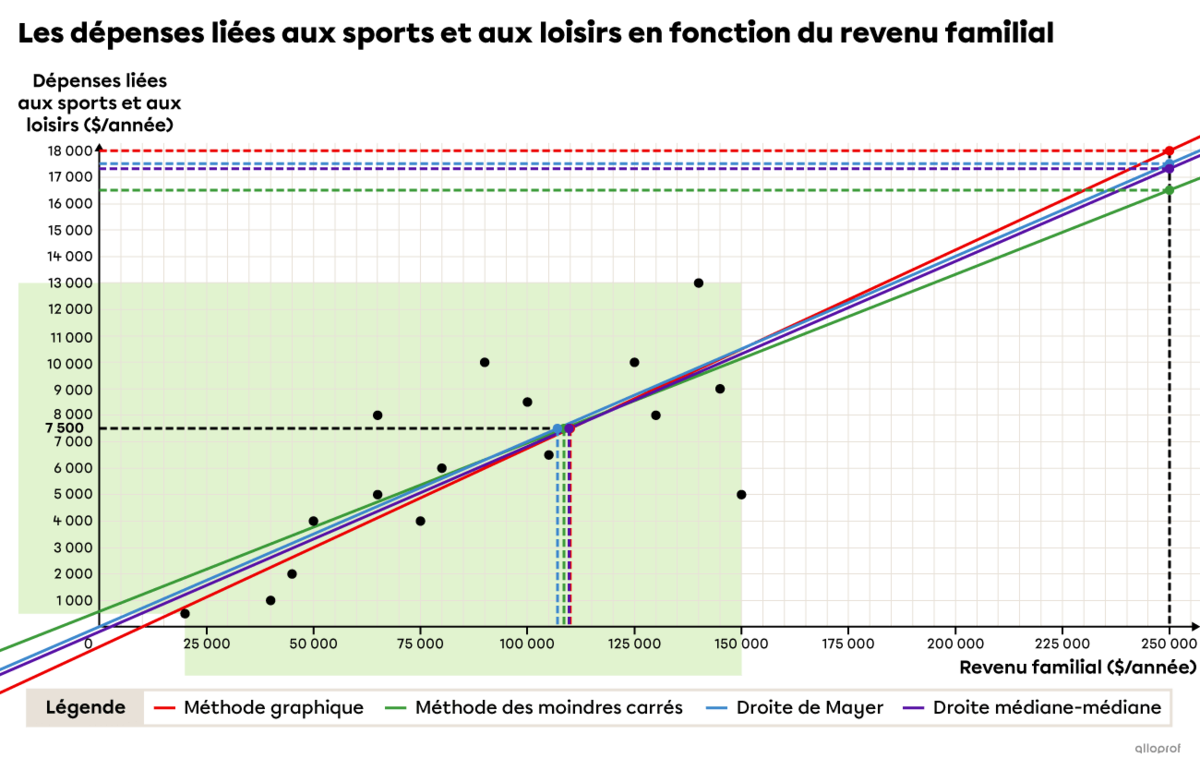
Pour l’extrapolation, les estimations varient de |16\ 511\ \$| à |18\ 000\ \$.| Pour l’interpolation, elles vont de |107\ 057\ \$| à |110\ 000\ \$.| Si le nuage de points avait présenté une meilleure corrélation, c’est-à-dire avec un coefficient de corrélation |(r)| plus près de |1,| les prédictions auraient été encore plus proches l’une de l’autre.
Finalement, comme il n’y a pas de données aberrantes dans la distribution de données, on ne peut pas dire que la méthode de la droite de Mayer est moins fiable que les autres.