Matières
Niveaux
La longueur est une grandeur servant à mesurer un objet dans le sens de sa plus grande dimension.
En plus de permettre de mesurer la plus grande dimension d'un objet, on utilise aussi la longueur pour mesurer physiquement la distance entre deux objets.
Différentes unités de mesure de la longueur existent. Avant 1971, le système impérial était le système officiel utilisé au Canada. Ce système a comme unités de mesure le pied, le pouce et l'once, entre autres. Toutefois, depuis 1971, le Canada a adopté officiellement le système métrique, basé sur le mètre.
L'unité de mesure de base de la longueur, dans le système international (SI), est le mètre (m).
Voici un tableau des unités les plus souvent utilisées :
| Préfixe | kilo- | hecto- | déca- | | déci- | centi- | milli- |
|---|---|---|---|---|---|---|---|
| Longueur | kilomètre (km) | hectomètre (hm) | décamètre (dam) | mètre (m) | décimètre (dm) | centimètre (cm) | millimètre (mm) |
| Valeur équivalente à 1 mètre | 0,001 | 0,01 | 0,1 | 1 | 10 | 100 | 1 000 |
Dans ce tableau, chaque unité est 10 fois plus grande que l'unité qui la suit. Ainsi, 1 mètre mesure 10 décimètres, 1 décimètre mesure 10 centimètres, et ainsi de suite.
On utilise le kilomètre (km) pour mesurer des distances parcourues en voiture.
On utilise le mètre (m) pour mesurer des bâtiments.
On utilise le centimètre (cm) pour mesurer des objets comme un crayon ou un bureau.
On utilise le millimètre (mm) pour mesurer de très petits objets.
La conversion d'une unité de mesure consiste à exprimer une grandeur dans une unité de mesure inférieure ou supérieure.
On peut utiliser la méthode des bonds ou encore le tableau des unités de mesure pour convertir une mesure en une autre.

On peut utiliser la méthode des bonds ou encore le tableau des unités de mesure pour convertir une mesure en une autre.
Selon cette méthode, il faut :
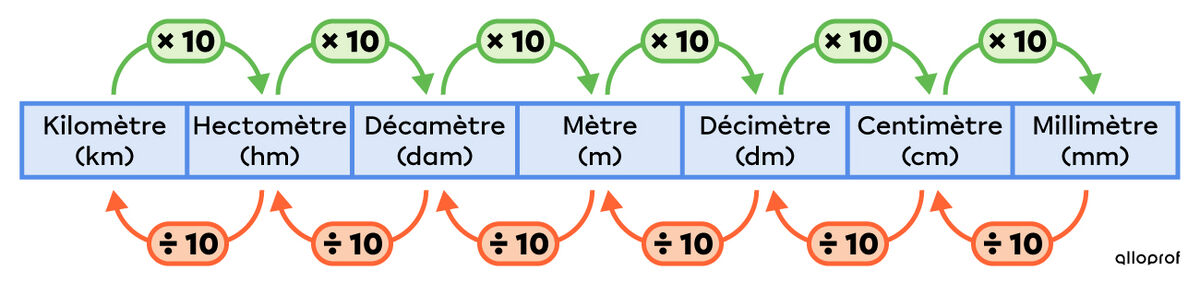
multiplier l'unité par 10 lorsqu'on la transforme en une unité plus petite;
diviser l'unité par 10 lorsqu'on la transforme en une unité plus grande.
Il faut multiplier ou diviser par 10 autant de fois qu'on se déplace de position.
On veut convertir 2,3 kilomètres en mètres.
Pour passer de km à m, on multiplie par 10 à chaque changement d'unité.

|2{,}3\ \text{km}\times10 = 23\ \text{hm}|
|23\ \text{hm}\times10 = 230\ \text{dam}|
|230\ \text{dam}\times10 = 2\ 300\ \text{m}|
OU
|2{,}3\times10\times10\times10 = 2{,}3\times 1\ 000 = 2\ 300\ \text{m}|
Réponse : |2{,}3\ \text{km} = 2\ 300\ \text{m}|
Selon cette méthode, il faut :
placer l'unité du nombre à la position de l'unité de mesure donnée et on place les autres nombres à gauche de celui-ci;
mettre un 0 dans chaque colonne jusqu’à la colonne de l'unité de mesure recherchée.
On veut convertir 34 mètres en centimètres.
Le chiffre 4 est l'unité du nombre, on place donc ce chiffre à la position des mètres dans le tableau.
On place le 3 dans la colonne à gauche des mètres, car il est à gauche du 4 dans le nombre de départ.
On met des 0 dans chaque colonne de droite, et ce, jusqu’à la colonne des centimètres (puisque l'objectif est de convertir en centimètres).
On obtient le nombre 3 400. Il y a effectivement 3 400 cm dans 34 m.

Lorsque l'on passe d'une unité de mesure plus petite à une unité plus grande, on doit mettre une virgule dans la colonne de l'unité de mesure recherchée.
On veut convertir 17 millimètres en mètres.
On place le 1 dans la colonne à gauche des millimètres, car il est à gauche du 7 dans le nombre de départ.

On ajoute ensuite un 0 dans chaque colonne jusqu’à la colonne des mètres (puisque l'objectif est de convertir en mètres).
On ajoute finalement une virgule dans la colonne des mètres à la droite du 0. On obtient ainsi le nombre 0,017 m. Il y a effectivement 0,017 mètre dans 17 millimètres.