Matières
Niveaux
Le volume représente l'espace occupé par un solide. On exprime le volume d'un solide en unités cubes.
Grâce au volume, on peut déterminer la portion de l'espace qui est occupée par un objet. On mesure généralement le volume pour les solides, mais il est aussi possible de le déterminer pour un liquide. On parlera dans ce cas de capacité.
L'unité de mesure de base du volume, dans le système international (SI), est le mètre cube (m3).
Voici un tableau des unités de volume les plus souvent utilisées :
| Préfixe | kilo- | hecto- | déca- | déci- | centi- | milli- | |
|---|---|---|---|---|---|---|---|
| Volume | kilomètre cube |(\text{km}^3)| | hectomètre cube |(\text{hm}^3)| | décamètre cube |(\text{dam}^3)| | mètre cube |(\text{m}^3)| | décimètre cube |(\text{dm}^3)| | centimètre cube |(\text{cm}^3)| | millimètre cube |(\text{mm}^3)| |
| Valeur équivalente en mètre cube | |0{,}000\, 000\, 001| | |0{,}000\, 001| | |0{,}001| | |1| | |1\, 000| | |1\, 000\, 000| | |1\, 000\, 000\, 000| |
Dans ce tableau, chaque unité est 1 000 fois plus grande que l'unité qui la suit. Ainsi, 1 mètre cube vaut 1 000 décimètres cubes, 1 décimètre cube vaut 1 000 centimètres cubes, et ainsi de suite.
Pour passer d'une unité de mesure à l'autre, pour des unités de volume, on doit multiplier ou diviser par 1 000.
Contrairement aux mesures de longueur, les unités de volume diffèrent entre elles d'un facteur 1 000.
Prenons par exemple deux cubes dont les mesures de côtés respectives sont : 1 cm et 10 mm. Ces deux cubes ont donc les mêmes dimensions, mais elles sont exprimées dans des unités différentes.
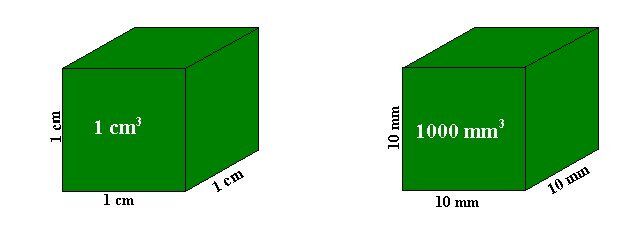
- Le volume du premier cube : 1 cm × 1 cm × 1 cm = 1 cm3
- Le volume du deuxième cube : 10 mm × 10 mm × 10 mm = 1 000 mm3
On remarque que 1 cm = 10 mm mais que 1 cm3 = 1 000 mm3.
On peut utiliser la méthode des bonds ou encore le tableau des unités de mesure pour convertir une mesure en une autre.
Selon cette méthode, il faut :
multiplier par 1 000 à chaque bond (à chaque changement d'unité) pour passer d'une unité plus grande à une unité plus petite;
diviser par 1 000 à chaque bond (à chaque changement d'unité) pour passer d'une unité plus petite à une unité plus grande.
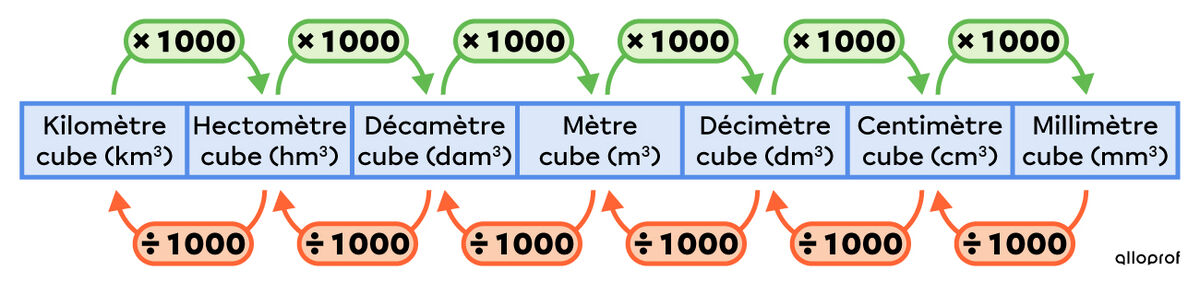

|14{,}58\ \text{m}^3\times1\ 000=14\ 580\ \text{dm}^3|
|14\ 580\ \text{dm}^3\times1\ 000=14\ 580\ 000\ \text{cm}^3|
ou
|14{,}58\ \text{m}^3\times1\ 000\times1\ 000=14\ 580\ 000\ \text{cm}^3|
Réponse : |14{,}58\ \text{m}^3 = 14\ 580\ 000\ \text{cm}^3|
Selon cette méthode, il faut :
placer l'unité, la dizaine et la centaine du nombre à la position de l'unité de mesure donnée et on place les autres nombres (s'il y en a) à gauche de celui-ci, et ce, toujours en paquet de trois;
mettre trois 0 dans chaque colonne jusqu’à la colonne de l'unité de mesure recherchée.
On doit toujours mettre trois chiffres dans chaque case avant de changer de colonne.
On veut convertir 234 m3 en cm3.
1. On place le 2 (centaine), le 3 (dizaine) et le 4 (unité) dans la colonne des m3 (puisque c'est l'unité de mesure de départ).
2. On met trois 0 dans chaque colonne jusqu’à la colonne des cm3 (puisque l'objectif est de convertir en cm3).
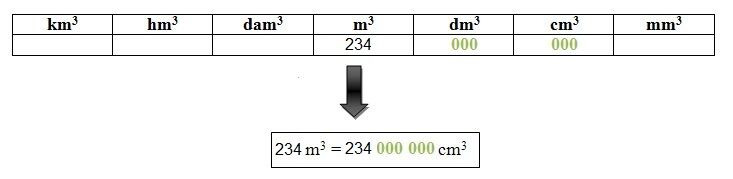
234 m3 = 234 000 000 cm3
Lorsque l'on passe d'une unité de mesure plus petite à une unité plus grande, on doit mettre une virgule dans la colonne de l'unité de mesure recherchée.
On veut convertir 7 569 800 mm3 en m3.
1. On place le 8 (centaine), le 0 (dizaine) et le 0 (unité) dans la colonne des mm3 (puisque le nombre de départ est exprimé en mm3).
2. On place, en paquet de trois, les autres nombres en se déplaçant vers la gauche pour ensuite ajouter les 0 nécessaires afin de parvenir à l'unité de mesure recherchée (le m3 dans ce cas-ci).

3. On ajoute une virgule dans la colonne des m3.

On obtient 0,007 569 800 m3 ou 0,007 569 8 m3
Il est possible de transformer les unités de volume en unités de capacité. Pour cela, on doit retenir quelques relations importantes.
|1\ \text{m}^3 = 1\ \text{kL}|
|1\ \text{dm}^3 = 1\ \text{L}|
|1\ \text{cm}^3 = 1\ \text{mL}|

On veut transformer 125 hm3 en hL.
1. On doit transformer les hL en l’une des trois unités connues (voir l'encadré précédent): m3, dm3 ou cm3.
125 hm3 × 1 000 = 125 000 dam3
125 000 dam3 × 1 000 = 125 000 000 m3
2. On transforme les m3 en kL.
Étant donné que 1 m3 = 1 kL, on obtient que :
125 000 000 m3 = 125 000 000 kL
3. On transforme les kL en hL.
125 000 000 kL × 10 = 1 250 000 000 hL ou 1,25 × 109 hL
