Matières
Niveaux
La masse correspond à la quantité de matière contenue dans un objet. On mesure généralement la masse d'un objet à l'aide d'une balance.

Plus il y a de matière dans un objet et plus sa masse sera grande. Ainsi, la force nécessaire pour le déplacer sera plus importante. Il est important de ne pas se fier au volume d'un objet pour estimer sa masse. Par exemple, une brique a une plus grande masse qu'un oreiller même si son volume est plus petit.
L'unité de mesure de base de la masse, dans le système international (SI), est le kilogramme (kg).
Voici un tableau des unités les plus souvent utilisées :
| Préfixe | kilo- | hecto- | déca- | | déci- | centi- | milli- |
| Masse | kilogramme (kg) | hectogramme (hg) | décagramme (dag) | gramme (g) | décigramme (dg) | centigramme (cg) | milligramme (mg) |
| Valeur équivalente à 1 g | 0,001 kg | 0,01 hg | 0,1 dag | 1 g | 10 dg | 100 cg | 1 000 mg |
Dans ce tableau, chaque unité est 10 fois plus grande que l'unité qui la suit. Ainsi, 1 gramme vaut 10 décigrammes, 1 décigramme vaut 10 centigrammes, et ainsi de suite.
La conversion d'une unité de mesure consiste à exprimer une grandeur dans une unité de mesure inférieure ou supérieure.
On peut utiliser la méthode des bonds ou encore le tableau des unités de mesure pour convertir une mesure en une autre.

Selon cette méthode, il faut:
Il faut multiplier ou diviser par 10 autant de fois qu'on se déplace de position.

Par exemple, pour transformer des cg en mg, on doit multiplier par 10. À l’inverse, pour transformer des mg en cg, on doit diviser par 10.
Généralement, quand on se déplace vers des unités situées vers la droite, on multiplie par 10 à chaque bond effectué. Quand on se déplace vers des unités situées vers la gauche, on divise par 10 à chaque bond effectué.
On peut aussi utiliser un tableau pour faire les conversions.
Selon cette méthode, il faut:
Si on veut convertir 34 grammes en centigrammes, on place le chiffre situé à la position de l’unité (le 4) dans la colonne des grammes (unité de mesure de départ). On place ensuite le 3 dans la colonne des décagrammes. Finalement, il ne reste plus qu’à mettre des 0 dans chaque colonne jusqu’à la colonne des centigrammes (unité de mesure demandée).
On obtient 3 400 cg.
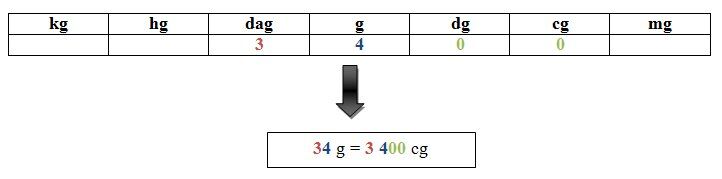
Il doit y avoir un chiffre dans toutes les colonnes, et ce, jusqu'à l'unité de mesure recherchée.
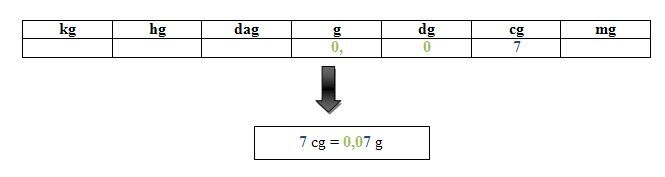
Souvent, on mesure la masse en livres. Il existe une petite opération mathématique pour convertir des kilogrammes en livres:
Livres |\approx| Kilogrammes x 2,2
Kilogrammes |\approx| Livres / 2,2
Aussi, si tu veux distinguer la masse et le poids, tu peux aller consulter cette fiche:
La masse et le poids.