Matières
Niveaux
Dans le type de problème présentant, par exemple, des situations impliquant des réseaux, il est souvent demandé de minimiser ou de maximiser les couts ou les distances. Il faut donc trouver l'arbre de la valeur minimale ou maximale qui relie entre eux tous les sommets d'un graphe.
Étapes de résolution d'un problème avec l'utilisation de l'arbre de valeur minimale:
Étapes de résolution d'un problème avec l'utilisation de l'arbre de valeur maximale:
Construction de trottoirs
Un entrepreneur doit relier 5 immeubles par des trottoirs de béton. Il soumet une première estimation du cout de l'opération, représenté par le graphe valué ci-contre. Les couts notés sont en milliers de dollars.
On veut minimiser le cout total de la construction de ces trottoirs en s'assurant que tous les immeubles soient reliés.
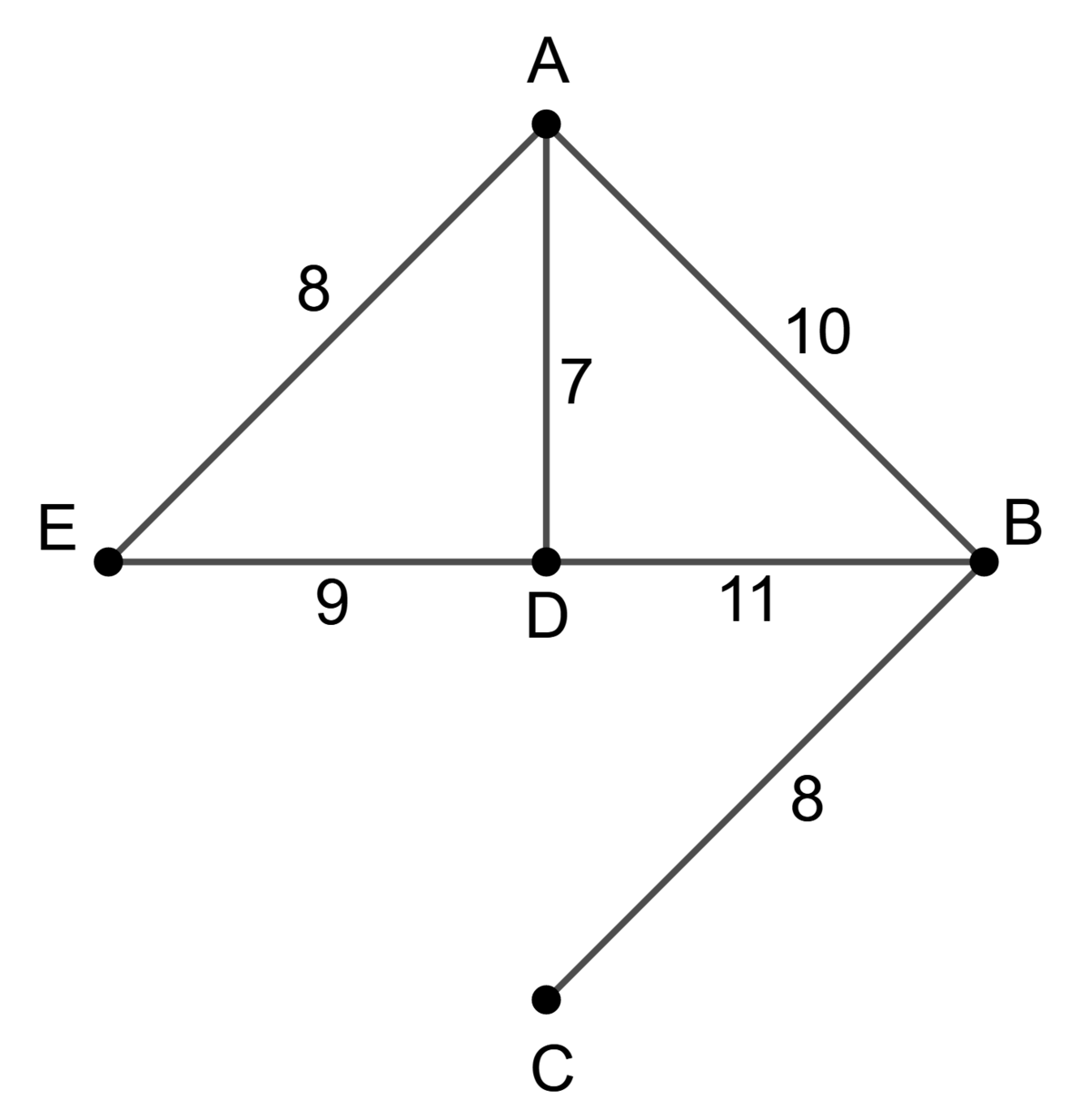
Solution
Comme on veut minimiser les couts, il faut donc déterminer l'arbre de valeur minimale.
Étape 1
Réécrire les sommets du graphe à côté du graphe de départ.
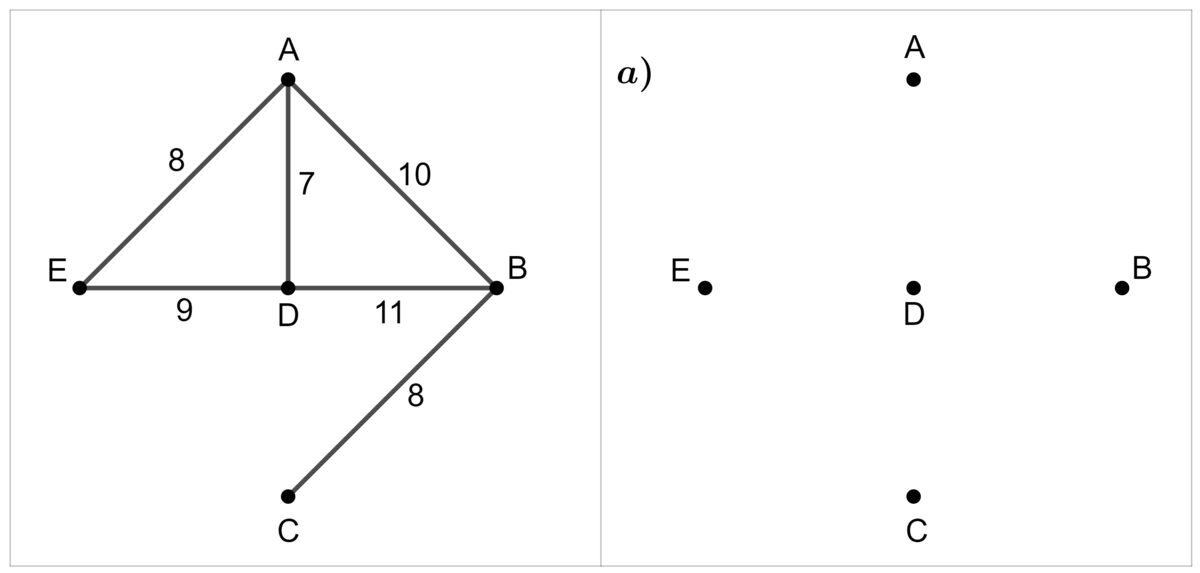
Étape 2
Tracer l'arête ayant le plus petit poids.
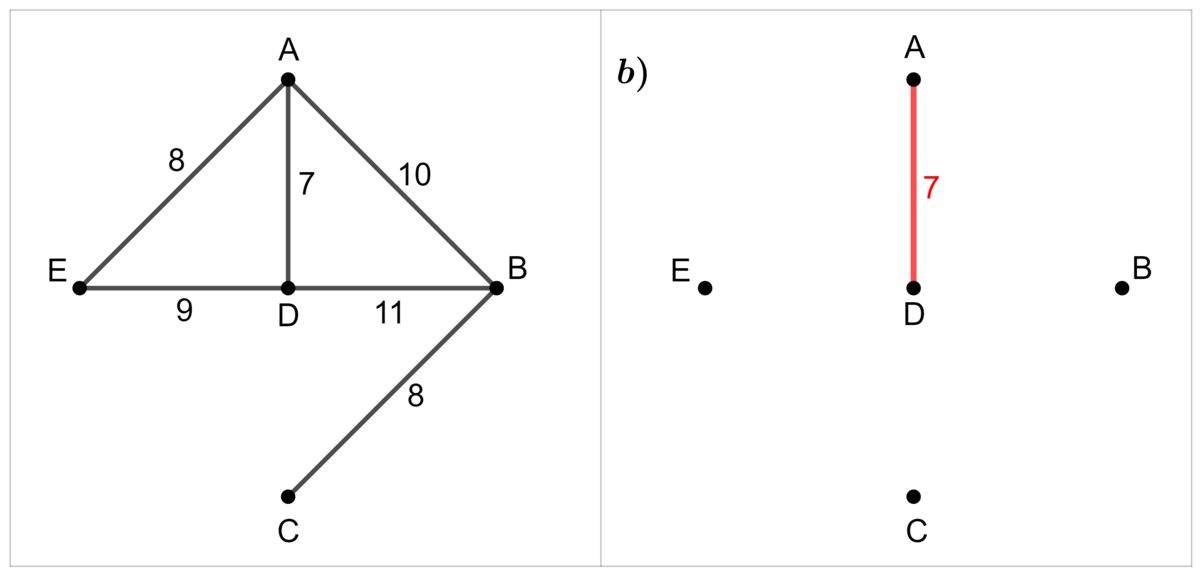
Étape 3
Parmi les arêtes restantes, répéter la deuxième étape jusqu'à ce que tous les sommets du graphe soient reliés sans cycle simple.
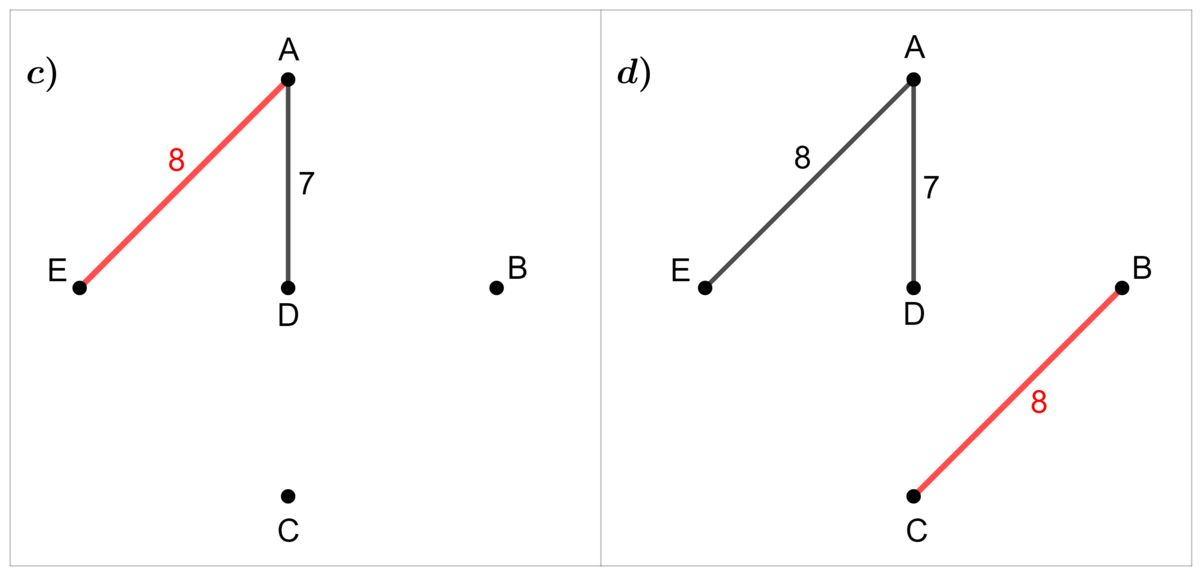
Puisque deux arêtes ont la même valeur, on les sélectionne tous les deux successivement s'ils ne créent pas de cycle simple. Puis, on continue avec la valeur suivante.
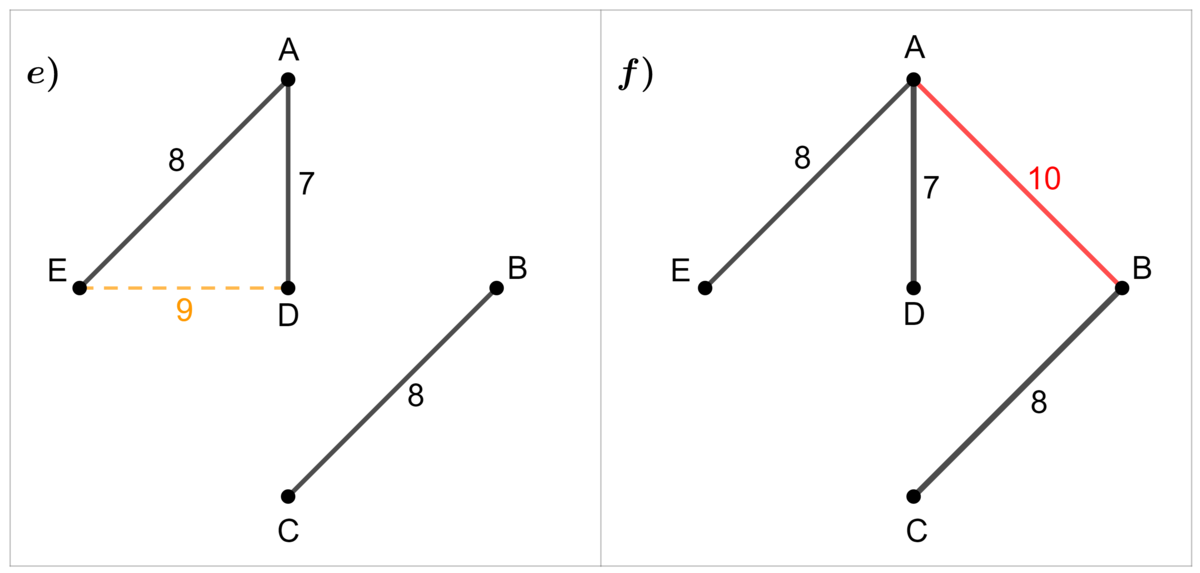
Puisque l'arête |\overline{ED}| créerait un cycle simple, on passe à la suivante.
Après avoir sélectionné le segment |\overline{AB}|, tous les sommets sont maintenant reliés. On a donc l'arbre de valeur minimale.
Étape 4
Calculer le poids de l'arbre obtenu.
Il suffit d'additionner la valeur de toutes les arêtes sélectionnées pour connaitre le cout total des travaux.
|\text{Cout}=7+8+8+10=33 \text{ milliers de dollars}=33\ 000| $