Matières
Niveaux
Une matrice est un arrangement de m lignes et de n colonnes de nombres. Dans une matrice A de dimension m × n :
|A=\left(\begin{array}{ccccc}
a_{11} & a_{12} & a_{13} & \ldots & a_{1n}\\
a_{21} & a_{22} & a_{23} & \ldots & a_{2n}\\
a_{31} & a_{32} & a_{33} & \ldots & a_{3n}\\
\vdots & \vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & a_{m3} & \ldots & a_{mn}
\end{array}\right)|
Une matrice est un tableau rectangulaire ordonné comportant des données disposées en lignes et en colonnes. Les matrices servent, entre autre, à exprimer des règles de transformation lorsqu'on applique des transformations géométriques au plan cartésien.
Soit le polygone ABCD suivant:
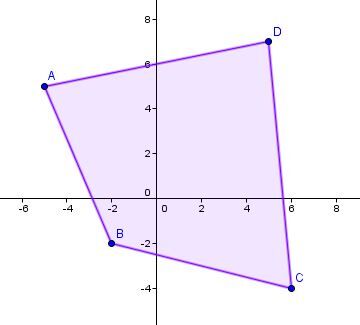
Les coordonnées des sommets du polygone peuvent être présentés séparément à l'aide de matrices colonnes:
|A=\begin{pmatrix}
-5\\
5
\end{pmatrix},
B=\begin{pmatrix}
-2\\
-2
\end{pmatrix},
C=\begin{pmatrix}
6\\
-4
\end{pmatrix}| et |D=\begin{pmatrix}
5\\
7
\end{pmatrix}|. Il est aussi possible d'écrire les coordonnées des sommets à l'aide de matrices lignes:
|A = \begin{pmatrix} -5 & 5 \end{pmatrix}, B= \begin{pmatrix} -2 & -2 \end{pmatrix}, C= \begin{pmatrix} 6 & -4 \end{pmatrix}| et |D=\begin{pmatrix} 5 & 7 \end{pmatrix}|.
ou dans une matrice: il est possible d'écrire la matrice de deux façons.
|M=\begin{pmatrix}
-5 & -2 & 6 & 5\\
5 & -2 & -4 & 7
\end{pmatrix}| ou |M=\begin{pmatrix} -5 & 5 \\ -2 & -2 \\ 6 & -4 \\ 5 & 7 \end{pmatrix}|
On désigne généralement une matrice par une lettre majuscule (par exemple la matrice |A|) et chaque élément qui la compose par une lettre minuscule.
La matrice |A| ci-dessous est composée de 2 lignes et de 3 colonnes. Cette matrice est de dimension |2 \times 3|.
|\begin{pmatrix}
2 & 5 & 4\\
-1 & 7 & -3
\end{pmatrix}|
On peut noter que : |a_{23} = -3| et |a_{13} = 4|
Certaines matrices portent des qualificatifs particuliers lorsqu'elles présentent certaines caractéristiques.
|0_{2\times 3}=\begin{pmatrix}
0 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}|
|A_{1\times 3}=\begin{pmatrix}
2 & 3 & 0
\end{pmatrix}|
|A_{3\times1}=\begin{pmatrix}
2\\
3\\
0
\end{pmatrix}|
|A_{4\times4}=\begin{pmatrix}
{\color{Green} 2} & 5 & 7 & -1\\
0 & {\color{Green} 3} & -4 & 5\\
1 & 3 & {\color{Green} 6} & 4\\
-2 & 0 & 4 & {\color{Green} 5}
\end{pmatrix}|
La diagonale principale de cette matrice est formée des éléments |2, 3, 6, 5|.
|A_{3\times3}=\begin{pmatrix}
3 & {\color{Red} 0} & {\color{Red} 0}\\
{\color{Red} 0} & -2 & {\color{Red} 0}\\
{\color{Red} 0} & {\color{Red} 0} & 4
\end{pmatrix}|
|I_{4\times4} = \begin{pmatrix}
{\color{Red} 1} & 0 & 0 & 0\\
0 & {\color{Red} 1} & 0 & 0\\
0 & 0 & {\color{Red} 1} & 0\\
0 & 0 & 0 & {\color{Red} 1}
\end{pmatrix}|
À noter: Dans la matrice identité, les éléments qui ne sont pas dans la diagonale principale ne peuvent pas être différents de 0.