Matières
Niveaux
Dans certains types de situation, il est possible de représenter les différentes étapes à l'aide d'un graphe valué et orienté. Ainsi, il sera visuellement possible de voir différents chemins partant tous du même point d'origine et se rendant au même point final. Certains de ces chemins peuvent être parallèles, ce qui signifie que les étapes qui les composent peuvent se dérouler en même temps. Parmi tous ces chemins, celui ayant le plus grand poids est le chemin critique. Le poids ici représente le temps minimal qu'il faut considérer pour réaliser le projet au complet.
Étapes de résolution d'un problème avec l'utilisation du chemin critique :
Représenter la situation à l'aide d'un graphe valué et orienté en tenant compte des étapes préalables.
Déterminer le poids de chacun des chemins qui relient le sommet du début et le sommet de la fin.
Le chemin critique du graphe correspond au chemin qui a le plus grand poids. Il suffit d'interpréter la réponse selon la situation.
Produire un album de finissant
Le comité des finissants d'une école secondaire se prépare à la production d'un album de finissants. La directrice de l'école leur demande d'estimer le temps requis pour la production de leur album. Voici un tableau qui présente les étapes à faire pour la réalisation de l'album de finissants.
| Tâches | Temps (jours) | Préalables |
| A : Acheter les films | 1 | Aucun |
| B : Charger les caméras | 1 | A |
| C : Prendre les photos du conseil étudiant | 3 | B |
| D : Prendre les photos des enseignants | 2 | B |
| E : Prendre les photos des clubs sportifs | 1 | B |
| F : Faire développer les photos | 2 | C-D-E |
| G : Faire la mise en page | 5 | F |
| H : Faire signer par le comité de l’album | 3 | G |
| I : Faire signer par la directrice | 2 | G |
| J : Imprimer les albums | 5 | H-I |
Déterminer le nombre minimum de jours requis pour la production de l'album de finissants.
Solution
Étape 1
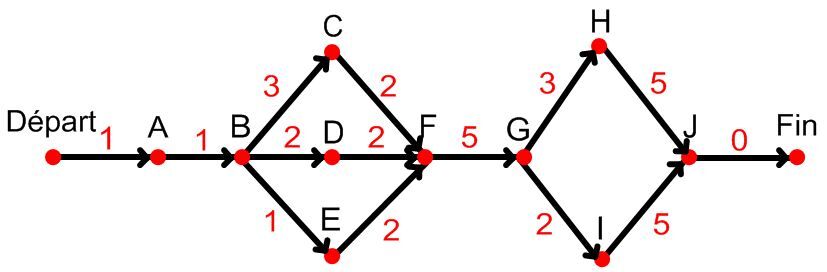
Étape 2
Début - A - B - C - F - G - H - J - Fin = 20
Début - A - B - C - F - G - I - J - Fin = 19
Début - A - B - D - F - G - H - J - Fin = 19
Début - A - B - D - F - G - I - J - Fin = 18
Début - A - B - E - F - F - H - J - Fin = 18
Début - A - B - E - F - G - I - J - Fin = 17
Étape 3
Dans cet exemple, le chemin critique est Début - A - B - C - F - G - H - J - Fin puisque son poids est le plus élevé, soit 20 jours. On peut donc affirmer que la production de l'album prendra au minimum 20 jours.