Matières
Niveaux
Dans le plan cartésien, une matrice de transformation est une matrice qui permet, à partir des coordonnées d'un point initial, de trouver celles de son image par une transformation géométrique donnée. Il faut à être à l'aise avec la multiplication de matrices.
Soit un point initial |(x,y)| et soit la matrice |\begin{bmatrix}
a & b\\
c & d
\end{bmatrix}| une matrice de transformation.
On obtient le point image |(x',y')| résultant de la transformation géométrique.
Ce point image se calcule ainsi:
|\begin{bmatrix}
a & b\\
c & d
\end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}|.
Il est possible d'effectuer diverses transformations géométriques grâce aux matrices.
Dans un plan cartésien, lorsque l'on veut effectuer un changement d'échelle horizontal de facteur |k|, on applique la transformation suivante:
|\begin{bmatrix} k & 0 \\0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
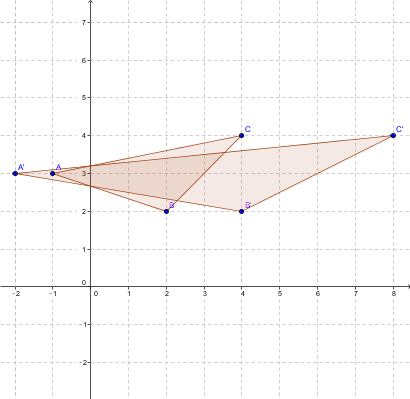
Soit le triangle |ABC| dont les sommets sont |A=(-1,3), B=(2,2)| et |C=(4,4)|. On veut effectuer un changement d'échelle horizontal de facteur |2|.
Pour trouver les sommets de la figure image, on effectue les calculs suivants:
|\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} -1 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ 3 \end{bmatrix}=A'|
|\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 2 \\ 2 \end{bmatrix} = \begin{bmatrix} 4 \\ 2 \end{bmatrix} = B'|
|\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 4 \\ 4 \end{bmatrix} = \begin{bmatrix} 8 \\ 4 \end{bmatrix} = C'|
On obtient le schéma suivant:
Dans un plan cartésien, lorsque l'on veut effectuer un changement d'échelle vertical de facteur |k|, on applique la transformation suivante:
|\begin{bmatrix} 1 & 0 \\0 & k \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
Soit le triangle |ABC| dont les sommets sont|A=(-1,3), B=(2,2)| et |C=(4,4)|. On veut effectuer un changement d'échelle vertical de facteur |3|.
Pour trouver les sommets de la figure image, on effectue les calculs suivants:
|\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} \times \begin{bmatrix} -1 \\ 3 \end{bmatrix} = \begin{bmatrix} -1 \\ 9 \end{bmatrix}=A'|
|\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} \times \begin{bmatrix} 2 \\ 2 \end{bmatrix} = \begin{bmatrix} 2 \\ 6 \end{bmatrix} = B'|
|\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} \times \begin{bmatrix} 4 \\ 4 \end{bmatrix} = \begin{bmatrix} 4 \\ 12 \end{bmatrix} = C'|
On obtient le schéma suivant:

Dans un plan cartésien, lorsque l'on veut effectuer une translation |t| selon un vecteur |\overrightarrow{t}(a,b)|, on applique la transformation suivante:
|\begin{bmatrix} x+a \\ y+b \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
On peut aussi utiliser la matrice de transformation |\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ a & b \end{bmatrix}|. Toutefois pour utiliser cette matrice, il faut former une autre matrice où chaque ligne correspond aux coordonnées d'un point et dont la dernière colonne est composée de seulement des |1|.
|\begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ a & b \end{bmatrix} = \begin{bmatrix} x_{1'} & y_{1'} \\ x_{2'} & y_{2'} \\ x_{3'} & y_{3'} \end{bmatrix}|
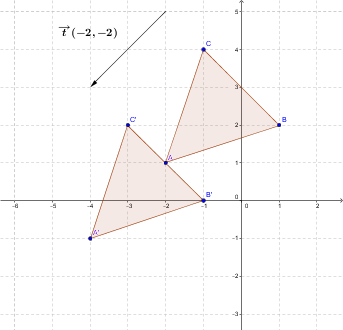
Soit le triangle |ABC| dont les sommets sont les points |A=(-2,1), B=(1,2)| et |C=(-1,4).| On veut effectuer une translation définie par le vecteur |\overrightarrow{t}(-2,-2).|
Ainsi, on obtient la transformation suivante:
|\begin{bmatrix} x-2 \\ y-2 \end{bmatrix}= \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et où |(x',y')| est le point image.
Pour trouver les sommets de la figure image, on effectue les calculs suivants:
|\begin{bmatrix} -2 -2 \\ 1 -2 \end{bmatrix} = \begin{bmatrix} -4 \\ -1 \end{bmatrix} =A'|
|\begin{bmatrix} 1 -2 \\ 2-2 \end{bmatrix} = \begin{bmatrix} -1 \\ 0 \end{bmatrix}=B'|
|\begin{bmatrix} -1 -2 \\ 4-2 \end{bmatrix} = \begin{bmatrix} -3 \\ 2 \end{bmatrix}=C'|
On obtient les mêmes coordonnées si on utilise la matrice de transformation de 3 lignes et 2 colonnes.
|\begin{bmatrix} -2 & 1 & 1 \\ 1 & 2 & 1 \\ -1 & 4 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ -2 & -2 \end{bmatrix} = \begin{bmatrix} -4 & -1 \\ -1 & 0 \\ -3 & 2 \end{bmatrix}|
On obtient le schéma suivant:
Dans un plan cartésien, lorsque l'on veut effectuer une réflexion |s| par rapport à l'axe des abscisses notée |s_x|, on applique la transformation suivante:
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
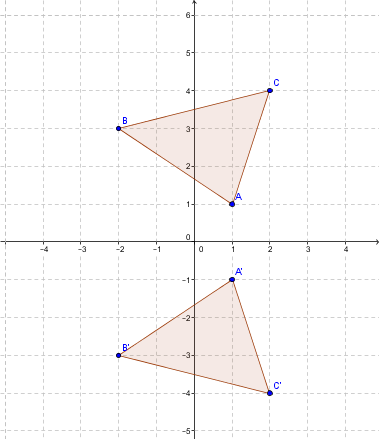
Soit le triangle |ABC| dont les sommets sont les points |A=(1,1), B=(-2,3)| et |C=(2,4)|. On veut effectuer une réflexion par rapport à l'axe des abscisses.
Pour trouver les sommets de la figure image, on effectue les calculs suivants:
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \end{bmatrix}=A'|
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} -2 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ -3 \end{bmatrix}=B'|
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} 2 \\ -4 \end{bmatrix} = C'|
On obtient le schéma suivant:
Dans un plan cartésien, lorsque l'on veut effectuer une réflexion |s| par rapport à l'axe des ordonnées notée |s_y|, on applique la transformation suivante:
|\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
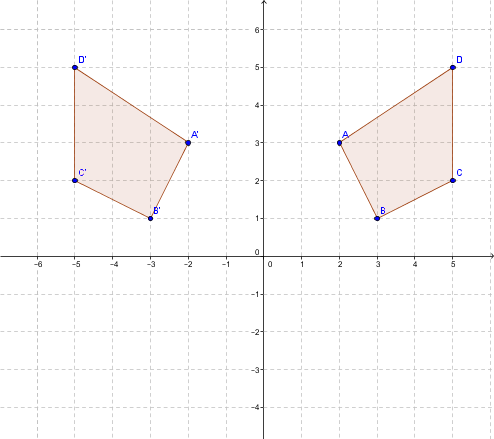
Soit le quadrilatère |ABCD| dont les sommets sont |A=(2,3)|, |B=(3,1)|, |C=(5,2)| et |D=(5,5)|. On veut effectuer une réflexion par rapport à l'axe des ordonnées.
Pour trouver les sommets de la figure image, on effectue les calculs suivants :
|\begin{bmatrix} -1 & 0 \\ 0 &1 \end{bmatrix} \times \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ 3 \end{bmatrix}=A'|
|\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} -3 \\ 1 \end{bmatrix} = B'|
|\begin{bmatrix}-1 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 5 \\ 2 \end{bmatrix} = \begin{bmatrix} -5 \\ 2 \end{bmatrix}=C'|
|\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 5 \\ 5 \end{bmatrix} = \begin{bmatrix} -5 \\ 5 \end{bmatrix} =D'|
On obtient le schéma suivant :
Dans un plan cartésien, lorsque l'on veut effectuer une rotation |r| d'un angle de |90| degrés (sens anti-horaire) centrée à l'origine, on applique la transformation suivante:
|\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
Soit le triangle |ABC| dont les sommets sont |A=(-3,3), B=(-1,0)| et |C=(2,4)|. On veut effectuer une rotation centrée à l'origine dont l'angle est de |90| degrés dans le sens anti-horaire.
Pour trouver les sommets de la figure image, on effectue les calculs suivants:
|\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} -3 \\ 3 \end{bmatrix} = \begin{bmatrix} -3 \\ -3 \end{bmatrix} =A'|
|\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} -1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ -1 \end{bmatrix} = B'|
|\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} -4 \\ 2 \end{bmatrix} = C'|
On obtient le schéma suivant:
Dans un plan cartésien, lorsque l'on veut effectuer une rotation |r| d'un angle de |180| degrés (sens anti-horaire) centrée à l'origine, on applique la transformation suivante:
|\begin{bmatrix} -1 & 0\\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
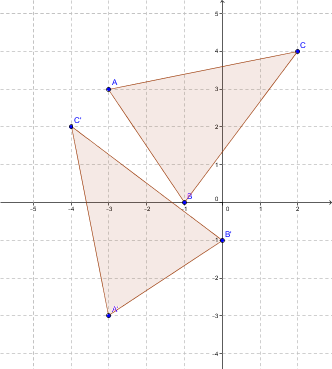
Soit le triangle |ABC| dont les sommets sont |A=(-4,1), B=(1,-2)| et |C=(3,3)|. On veut effectuer une rotation centrée à l'origine dont l'angle est de |180| degrés dans le sens anti-horaire.
Pour trouver les sommets de la figure image, on effectue les calculs suivants :
|\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} -4 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ -1 \end{bmatrix} =A'|
|\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} 1 \\ -2 \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} = B'|
|\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} 3 \\ 3 \end{bmatrix} = \begin{bmatrix} -3 \\ -3 \end{bmatrix} = C'|
On obtient le schéma suivant :
Dans un plan cartésien, lorsque l'on veut effectuer une rotation |r| d'un angle de |270| degrés (sens anti-horaire) centrée à l'origine, on applique la transformation suivante:
|\begin{bmatrix} 0 & 1\\-1 & 0 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
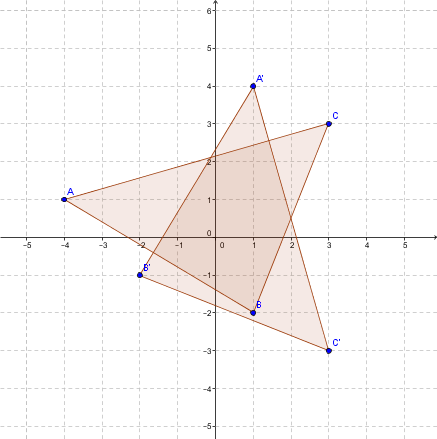
Soit le triangle |ABC| dont les sommets sont |A=(-4,1), B=(1,-2)| et |C=(3,3)|. On veut effectuer une rotation centrée à l'origine dont l'angle est de |270| degrés dans le sens anti-horaire.
Pour trouver les sommets de la figure image, on effectue les calculs suivants :
|\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \times \begin{bmatrix} -4 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 4 \end{bmatrix} =A'|
|\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \times \begin{bmatrix} 1 \\ -2 \end{bmatrix} = \begin{bmatrix} -2 \\ -1 \end{bmatrix} = B'|
|\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \times \begin{bmatrix} 3 \\ 3 \end{bmatrix} = \begin{bmatrix} 3 \\ -3 \end{bmatrix} = C'|
On obtient le schéma suivant :
Dans un plan cartésien, lorsque l'on veut effectuer une homothétie |h| centrée à l'origine de rapport |k|, on applique la transformation suivante:
|\begin{bmatrix} k & 0 \\ 0 & k \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| où |(x,y)| est le point initial et |(x',y')| est le point image.
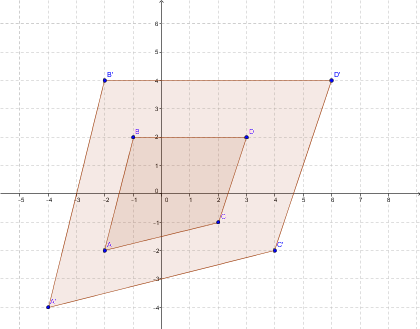
Soit le quadrilatère |ABCD| dont les sommets sont |A=(-2,-2)|, |B=(-1,2)|, |C=(2,-1)| et |D=(3,2)|. On veut effectuer une homothétie centrée à l'origine de rapport |k=2|.
Pour trouver les sommets de la figure image, on effectue les calculs suivants:
|\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \times \begin{bmatrix} -2 \\ -2 \end{bmatrix} = \begin{bmatrix} -4 \\ -4 \end{bmatrix}=A'|
|\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \times \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} -2 \\ 4 \end{bmatrix} = B'|
|\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \times \begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 4 \\ -2 \end{bmatrix} = C'|
|\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \times \begin{bmatrix} 3 \\ 2 \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \end{bmatrix} = D'|
On obtient le schéma suivant:
Pour effectuer une composition de transformations géométriques, on applique chaque transformation géométrique l'une après l'autre en commençant de gauche à droite. Par exemple pour |s_x \circ s_y|, il faut effectuer |s_y| puis ensuite |s_x|.
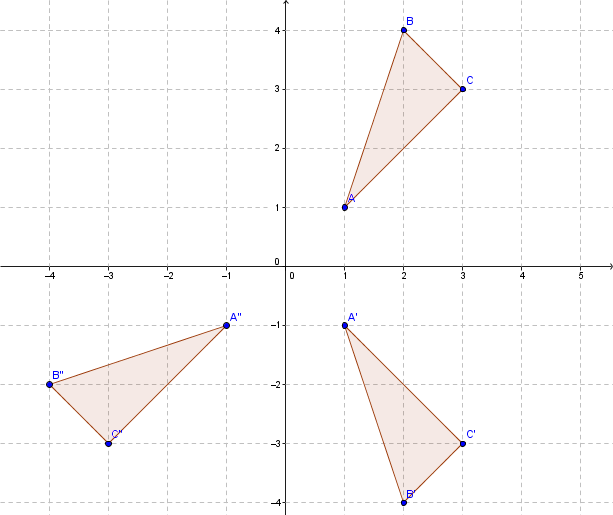
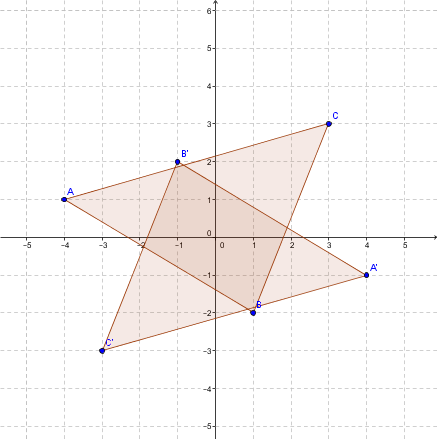
Soit le triangle |ABC| dont les sommets sont |A=(1,1), B=(2,4)| et |C=(3,3)|. On veut effectuer une réflexion par rapport à l'axe des abscisses suivie d'une rotation d'un angle de |270| degrés (sens anti-horaire) centrée à l'origine.
On note ceci |r_{270} \circ s_x|.
On effectue la réflexion par rapport à l'axe des abscisses:
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}|
On obtient alors:
|A'=(1,-1), B'=(2,-4)| et |C'=(3,-3)|.
Ensuite, on effectue la rotation d'un angle de 90 degrés (sens anti-horaire) centrée à l'origine:
|\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \times \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x'' \\ y'' \end{bmatrix}|
On obtient alors:
|A''=(-1,-1), B''=(-4,-2)| et |C''=(-3,-3)|.
On obtient le schéma suivant: