Matières
Niveaux
Un angle trigonométrique est un angle au centre dans le cercle trigonométrique qui résulte d’une rotation à partir de la partie positive de l’axe des abscisses (l’axe des |x|).
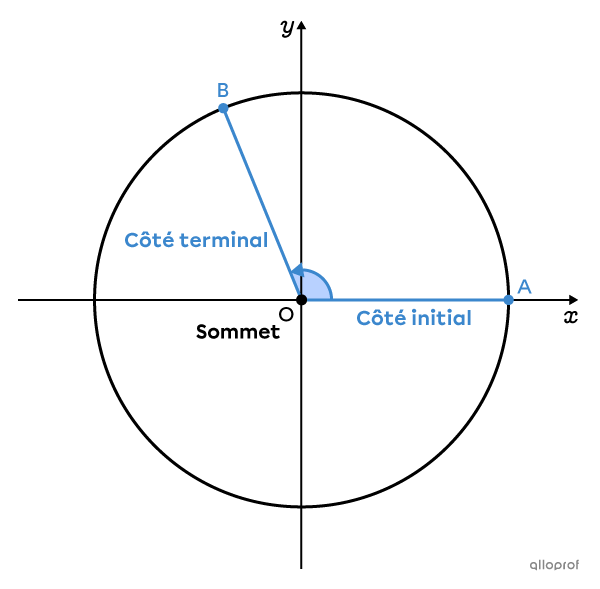
Dans un angle trigonométrique, on distingue 3 éléments :
le sommet |(O),| qui se situe au centre du cercle;
le côté initial |(\overline{AO}),| le côté de l'angle confondu avec l'axe des |x| positifs;
le côté terminal |(\overline{BO}),| le côté de l'angle obtenu par la rotation du côté initial autour du centre du cercle.
Remarque : Le côté initial et le côté terminal de l’angle sont des rayons du cercle trigonométrique.
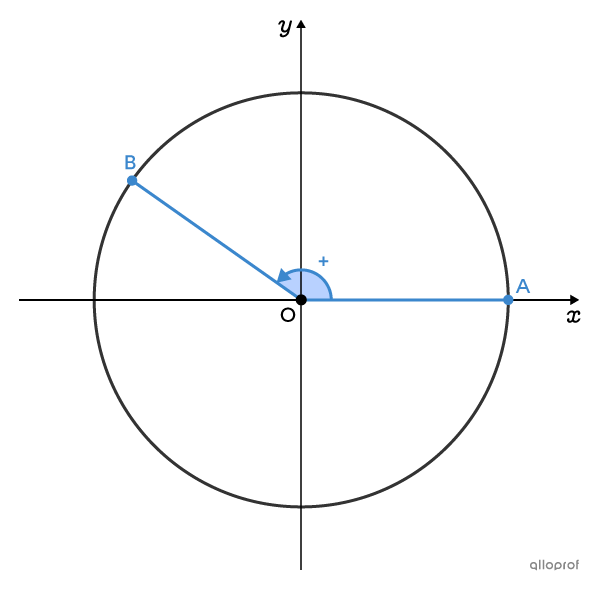
On peut analyser un même angle de 2 façons différentes : selon le sens antihoraire ou selon le sens horaire de rotation. Cela a un impact sur le signe de la valeur de l’angle.
Si la rotation du côté initial est effectuée dans le sens antihoraire, la mesure de l'angle est positive.
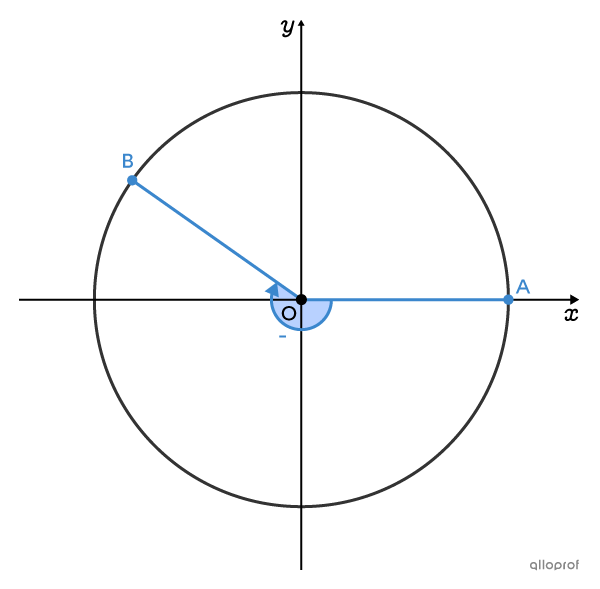
Si la rotation du côté initial est effectuée dans le sens horaire, la mesure de l'angle est négative.
Lorsqu’on travaille dans le cercle trigonométrique, on utilise les radians et non les degrés.
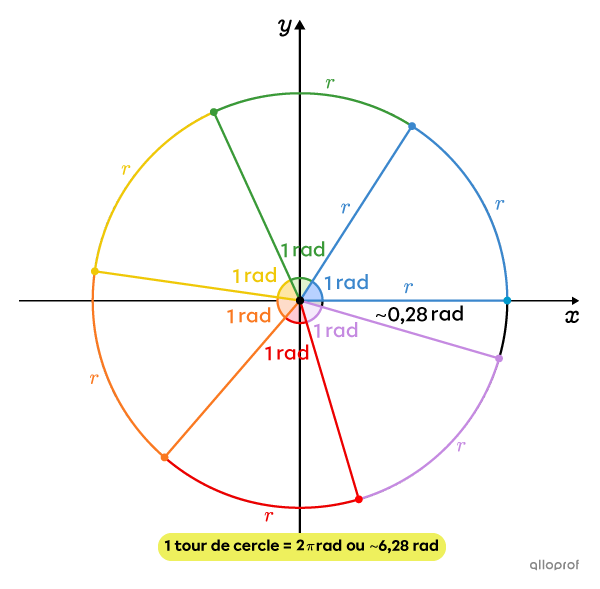
Un radian |(1\ \text{rad})| correspond à la mesure de l’angle au centre dont les côtés interceptent un arc de cercle dont la longueur est égale au rayon du cercle.
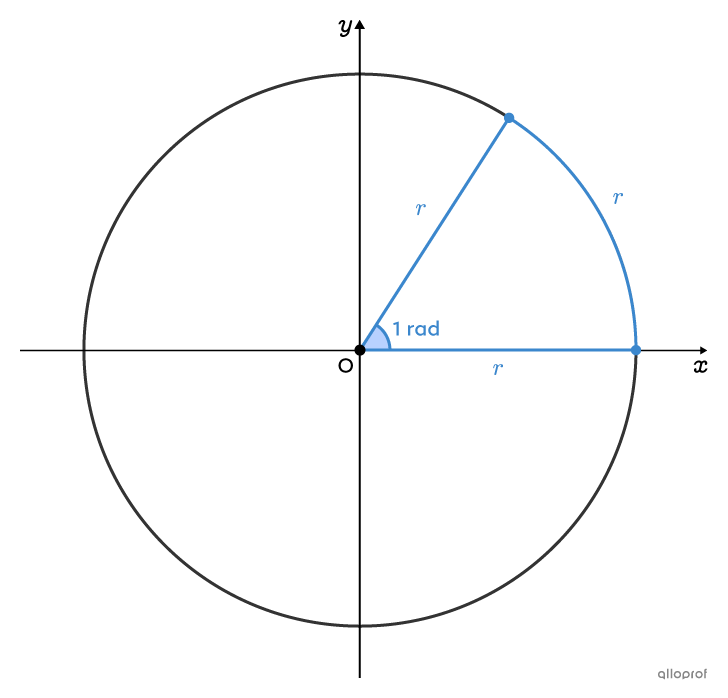
Pour trouver l’angle formé par un tour complet en radians, on résout l’équation suivante.||\begin{align}\dfrac{1\ \text{rad}}{?\ \text{rad}}&=\dfrac{\text{Arc de longueur équivalente à}\ 1\ \text{rayon}}{\text{Circonférence du cercle}}\\\\ \dfrac{1}{?}&=\dfrac{r}{2\pi r}\\\\?&=\dfrac{1 \times 2\pi r}{r}\\\\?&=2\pi\ \text{rad}\end{align}||On en déduit ainsi que l’angle formé par un tour complet vaut |2\pi\ \text{rad}\approx6{,}28\ \text{rad}.|
Sur l’image, on voit qu’il y a |6\ \text{rad}| complets qui entrent dans le cercle ainsi qu’une petite partie, qui représente environ |0{,}28\ \text{rad}.|
Sachant que |360^\circ=2\pi\ \text{rad},| on peut déterminer l’équivalence en radians de certains angles remarquables.
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{360^\circ}}{2}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi\ \text{rad}}}{2}}\\\\180^\circ&=\pi\ \text{rad}\end{align}||
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{360^\circ}}{4}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi\ \text{rad}}}{4}}\\\\90^\circ&=\dfrac{\pi}{2}\ \text{rad}\end{align}||
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{360^\circ}}{6}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi\ \text{rad}}}{6}}\\\\60^\circ&=\dfrac{\pi}{3}\ \text{rad}\end{align}||
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{360^\circ}}{12}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi\ \text{rad}}}{12}}\\\\30^\circ&=\dfrac{\pi}{6}\ \text{rad}\end{align}||
De cette façon, on peut déterminer l’équivalence en radians de plusieurs angles.
|
Angle en degrés |\boldsymbol{(^\circ)}| |
|30| |
|45| |
|60| |
|90| |
|120| |
|135| |
|150| |
|180| |
|210| |
|225| |
|240| |
|270| |
|300| |
|315| |
|330| |
|360| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Angle en radians |\boldsymbol{(\text{rad})}| |
|\dfrac{\pi}{6}| |
|\dfrac{\pi}{4}| |
|\dfrac{\pi}{3}| |
|\dfrac{\pi}{2}| |
|\dfrac{2\pi}{3}| |
|\dfrac{3\pi}{4}| |
|\dfrac{5\pi}{6}| |
|\pi| |
|\dfrac{7\pi}{6}| |
|\dfrac{5\pi}{4}| |
|\dfrac{4\pi}{3}| |
|\dfrac{3\pi}{2}| |
|\dfrac{5\pi}{3}| |
|\dfrac{7\pi}{4}| |
|\dfrac{11\pi}{6}| |
|2\pi| |
Pour passer d’une unité de mesure à l’autre, il faut établir une proportion. On y arrive en utilisant le fait qu’un tour de cercle complet équivaut à |2\pi\ \text{rad}| et à |360^\circ.|
||\dfrac{\text{Angle au centre en degrés}}{360^\circ}=\dfrac{\text{Angle au centre en radians}}{2\pi\ \text{rad}}||
Trouve la mesure d’un angle de |\dfrac{7\pi}{12}\ \text{rad}| en degrés.
||\begin{align}\dfrac{\theta}{360^\circ}&=\dfrac{\color{#3a9a38}{\frac{7\pi}{12}\ \text{rad}}}{2\pi\ \text{rad}}\\\\ \theta&=\dfrac{360\times \frac{7\pi}{12}}{2\pi}\\ \theta&=105^\circ\end{align}||
Réponse : La mesure de l’angle est de |105^\circ.|
Trouve la mesure d’un angle de |144^\circ| en radians.
||\begin{align}\dfrac{\color{#3a9a38}{144^\circ}}{360^\circ}&=\dfrac{\theta}{2\pi\ \text{rad}}\\\\ \theta&=\dfrac{144 \times 2\pi}{360}\\\theta&=\dfrac{4\pi}{5}\ \text{rad}\end{align}||
Réponse : La mesure de l’angle est de |\dfrac{4\pi}{5}\ \text{rad}.|
Pour déterminer la mesure d’un arc de cercle, on utilise la proportion suivante.||\begin{align}\dfrac{\text{Angle au centre en degrés}}{360^\circ}&=\dfrac{\text{Arc de cercle intercepté}}{\text{Circonférence du cercle}}\\\\ \dfrac{\theta}{360^\circ}&=\dfrac{L}{2\pi r}\end{align}||Puisque |360^\circ| équivaut à |2\pi| radians, on obtient la proportion suivante, qu’on réduit.||\begin{align}\dfrac{\theta\ \text{rad}}{\cancel{2\pi}\ \text{rad}}&=\dfrac{L}{\cancel{2\pi} r}\\\\ \dfrac{\theta\ \text{rad}}{1\ \text{rad}}&=\dfrac{L}{r}\end{align}||En manipulant la proportion ci-dessus, on trouve la formule suivante.
|L=\theta \times r|
où
|\begin{align}L&:\text{longueur de l'arc de cercle}\\\theta&:\text{angle au centre en radians}\\r&:\text{rayon}\end{align}|

Ainsi, les côtés d’un angle au centre de |\theta\ \text{rad}| interceptent un arc dont la longueur |(L)| correspond à |\theta| multiplié par le rayon |r.|
À l’aide de la formule |L=\theta \times r,| donne le rayon d’un cercle dont la mesure de l’angle au centre et la longueur de l’arc intercepté par cet angle sont |220^\circ| et |15\ \text{cm}.|
On transforme d’abord |220^\circ| en radians.||\begin{align}\dfrac{\color{#3a9a38}{220^\circ}}{360^\circ}&=\dfrac{\theta}{2\pi\ \text{rad}}\\\\
\dfrac{220\times 2\pi}{360}&=\theta\\\\ \dfrac{11\pi}{9}\ \text{rad}&=\theta\end{align}||On peut maintenant trouver le rayon.||\begin{align}L&=\theta\times r\\15&=\dfrac{11\pi}{9}\times r\\15\times{\frac{9}{11\pi}}&=r\\3{,}91\ \text{cm}&\approx r\end{align}||
Réponse : Le rayon est d’environ |3{,}91\ \text{cm}.|