Matières
Niveaux
Il est possible de réduire une expression algébrique en multipliant les termes qu'elle contient. Multiplier deux polynômes ensemble revient à multiplier chacun des termes du premier polynôme par chacun des termes du second.
On peut définir trois étapes à suivre pour la multiplication d'expressions algébriques :
Réduire l'expression, s'il y a lieu, en additionnant ou en soustrayant les termes semblables (avant d'effectuer la multiplication).
Effectuer les multiplications.
Réduire l'expression obtenue, s'il y a lieu, en additionnant ou en soustrayant les termes semblables.
Pour effectuer la multiplication d'expressions algébriques, deux règles importantes sont à suivre : ces règles se basent sur la commutativité de la multiplication.
A. On multiplie les nombres entre eux et les variables entre elles. ||3x \times 4y = 3 \times 4 \times x\times y = 12xy|| B. Lorsqu'on multiplie ensemble deux variables identiques, on additionne leur exposant. ||x^2y^3\times x^3y^7 = x^2 \times x^3 \times y^3\times y^7 = x^{(2+3)}\times y^{(3+7)} = x^5y^{10}||
Tous les termes, qu'ils soient semblables ou non, peuvent être multipliés entre eux. Par contre, seuls les termes semblables peuvent être additionnés ou soustraits ensemble.
Il est rare qu'une équation soit formée uniquement de multiplications. Il faudra, dans ce cas, respecter la priorité des opérations lors de la réduction de l'expression algébrique.
Pour multiplier des expressions algébriques, il est essentiel de bien maitriser les propriétés et les lois des exposants. De plus, on doit appliquer le principe de la distributivité. Lors de la multiplication d'expressions algébriques, plusieurs situations peuvent se présenter :
Lorsqu’on multiplie un monôme par un monôme, on multiplie les coefficients ensemble et on additionne les exposants des variables identiques.
Lorsqu’on multiplie un terme constant par un monôme, on multiplie le coefficient du monôme par le terme constant.
Soit le terme constant |-3| et le monôme |4xy^2|.
Effectue la multiplication |-3\times 4xy^2|.
On multiplie le terme constant avec le coefficient du monôme : ||-3 \times 4 = -12||On inscrit la réponse finale en ajoutant les variables mises de côté temporairement: ||-3\times 4xy^2 = -12xy^2||
Lorsqu’on multiplie deux monômes ensemble, on multiplie les coefficients des deux monômes et on additionne les exposants affectant les variables identiques.
Soit les deux monômes suivants : |-3x^3y^4| et |4xy^2|.
On effectue la multiplication |-3x^{3}y^4\times 4xy^2|.
On multiplie ensemble les coefficients : ||-3\times 4 = -12||
On additionne les exposants des mêmes variables : ||x^{(3+1)}\quad \text{et}\quad y^{(4+2)}||
On inscrit la réponse finale : ||-3x^{3}y^4\times 4xy^{2} = -12x^{4}y^{6}||
Voici la démarche détaillée : ||\begin{align} -3x^{3}y^4 \times 4xy^2 &= (-3\times {4}) {(x^{3}\times {x})}{(y^{4}\times {y^{2}})}\\
&=(-12){(x^{3+1})}{(y^{4+2})}\\
&=(-12){(x^{4})}{(y^{6})}\\
&=-12x^{4}y^{6}\end{align}||
Lorsqu’on multiplie un monôme par un polynôme, on applique la distributivité de la multiplication sur l’addition et le monôme multiplie alors chacun des termes du polynôme.
Pour chacune des multiplications, il faut multiplier les coefficients entre eux.
Pour chacune des multiplications, il faut additionner les exposants des mêmes variables.
Il est important de mettre entre parenthèses le polynôme.
Soit le terme constant |1{,}5| et le polynôme |2xy-x+5y|.
On effectue la multiplication en plaçant le polynôme entre parenthèses : ||1{,}5 (2xy-x+5y)||
On applique la distributivité de la multiplication sur l'addition et le terme constant multiplie alors chacun des termes du polynôme : ||\begin{align}\color{red}{1{,}5}(\color{blue} {2xy}\color{green} {-x}\color{fuchsia} {+5y}) &= (\color{red} {1{,}5}\times \color{blue} {2xy}) + (\color{red} {1{,}5}\times \color{green} {-x})+(\color{red} {1{,}5}\times \color{fuchsia} {+5y})\\ &= 3xy + -1{,}5x + 7{,}5y \\ &= 3xy - 1{,}5x + 7{,}5y \end{align}||
Soit le monôme |-3x^3y^4| et le binôme |4xy^2+2xy.| On effectue la multiplication en plaçant le binôme entre parenthèses : ||-3x^{3}y^{4}(4xy^{2} + 2xy)||
On applique la distributivité de la multiplication sur l’addition et le monôme multiplie alors chacun des termes du binôme.
La démarche détaillée s'effectue de la façon suivante : ||\begin{align}\color{red} {-3x^3y^4} (\color{blue} {4xy^2}\color{green} {+2xy}) &= (\color{red} {-3x^3y^4}\times \color{blue} {4xy^2}) + (\color{red} {-3x^3y^4}\times \color{green} {2xy}) \\ &= -12x^{4}y^{6}+(-6x^4y^5)\\&=-12x^4y^6-6x^4y^5\end{align}||

Moments dans la vidéo :
Lorsqu’on multiplie un polynôme par un polynôme, on applique la distributivité de la multiplication sur l’addition et chacun des termes du premier binôme multiplie chacun des termes du deuxième binôme.
Pour chacune des multiplications, il faut multiplier ensemble les coefficients.
Pour chacune des multiplications, il faut additionner les exposants des mêmes variables.
Il est important de mettre des parenthèses autour de chaque polynôme.
Soit le polynôme |-3x^3y^4+y| et le binôme |4xy^2+2xy.| On effectue la multiplication en plaçant les deux polynômes entre parenthèses : ||(-3x^{3}y^{4} + y){(4xy^{2} + 2xy)}||
On applique la distributivité de la multiplication sur l’addition et chacun des termes du premier binôme multiplie chacun des termes du deuxième binôme.
La démarche détaillée s'effectue de la façon suivante : ||(-3x^{3}y^{4} \times{4xy^{2}}) + (-3x^{3}y^{4}\times {2xy}) + (y\times {4xy^{2}}) + (y\times {2xy})|| ||=(-12x^{4}y^{6}) + (-6x^{4}y^{5}) + (4xy^{3}) + (2xy^{2})||
La réponse est donc : |-12x^{4}y^{6} - 6x^{4}y^{5} + 4xy^{3} + 2xy^{2}.|
Aussitôt que l’on multiplie un polynôme par un autre polynôme, chacun des termes du premier polynôme doit multiplier chacun des termes du deuxième polynôme.
||\begin{align} &(-3x^{3}y^{4} + 1) {(4xy^{2} + 2xy - 9x + 2y)} \\\\ =\ &(-3x^{3}y^{4}\times 4xy^{2}) +(-3x^{3}y^{4}\times {2xy}) + (-3x^{3}y^{4}\times {-9x}) + (-3x^{3}y^{4}\times {2y})\\ &+ (1\times {4xy^{2}}) + (1\times {2xy}) + (1\times {-9x}) + (1\times {2y})\\ \\ =\ &(-12x^{4}y^{6}) + (-6x^{4}y^{5}) + (27x^{4}y^{4}) + (-6x^{3}y^{5}) \\ &+ (4xy^{2}) + (2xy) + (-9x) + (2y)\\ \\ =\ &-12x^{4}y^{6} - 6x^{4}y^{5} + 27x^{4}y^{4} - 6x^{3}y^{5} + 4xy^{2} + 2xy - 9x + 2y\end{align}||

Moments dans la vidéo :
La multiplication d'expressions algébriques peut s'effectuer de façon plus visuelle, à l'aide de ce qu'on appelle des tuiles algébriques.
Multiplication d'un terme constant et d'un monôme à l'aide de tuiles algébriques
Soit le terme constant |3| et le monôme |x.| On effectue la multiplication |3\times x.| On peut représenter cette multiplication de la manière suivante :
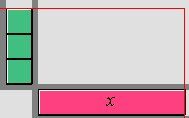
Ici, les trois cases vertes représentent le terme constant |3| et le rectangle rose représente le monôme |x.|
On multiplie chaque terme de la colonne par chaque terme de la ligne. Le produit obtenu est représenté par la surface délimitée par le rectangle formé.
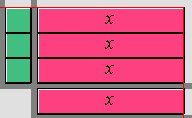
Comme le rectangle est formé par trois monômes |x,| la réponse est |3x.|
Multiplication de deux monômes à l'aide de tuiles algébriques
Soit un monôme |x| et un autre monôme |x.| On effectue la multiplication |x\times x.| On peut représenter cette multiplication de la manière suivante :
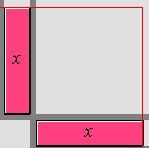
Ici, les deux rectangles roses représentent les monômes |x.|
On multiplie chaque terme de la colonne par chaque terme de la ligne. Le produit obtenu est représenté par la surface délimitée par le rectangle formé.
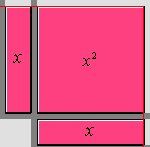
Comme le rectangle est formé par la combinaison de deux monômes |x,| la réponse est |x^2.|
Multiplication d'un monôme et d'un binôme à l'aide des tuiles algébriques
Soit le monôme |x| et le binôme |(y + 2).| On effectue la multiplication |x(y + 2).| On peut représenter cette multiplication de la manière suivante :
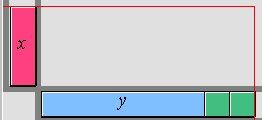
Ici, la colonne représente le monôme |x| et la ligne représente le polynôme |(y + 2),| soit le rectangle bleu pour la variable |y| et les deux carrés verts pour deux unités |(+2).|
On multiplie chaque terme de la colonne par chaque terme de la ligne. Le produit obtenu est représenté par la surface délimitée par le rectangle formé.

Comme les rectangles sont formés par la combinaison des variables |x| et |y,| et par deux monômes |x,| la réponse est |xy + 2x.|
Multiplication de deux polynômes à l'aide des tuiles algébriques
Soit les polynômes |(x + 1)| et |(x + 3).| On effectue la multiplication |(x + 1)(x + 3).| On peut représenter cette multiplication de la manière suivante :

Ici, la colonne représente le polynôme |(x + 1),| car la variable |x| est représentée par le rectangle rose et le chiffre 1 est représenté par le carré vert. La ligne représente le polynôme |(x + 3),| soit le rectangle rose pour la variable |x| et les trois carrés verts pour le chiffre |3.|
On multiplie chaque terme de la colonne par chaque terme de la ligne. Le produit obtenu est représenté par la surface délimitée par le rectangle formé.
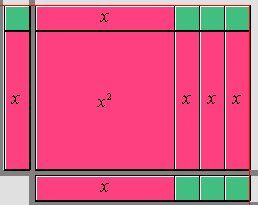
La réponse obtenue est : |x^{2} + 4x + 3.|