Trouver la règle d'une fonction exponentielle

Lorsqu'on cherche la règle d'une fonction exponentielle à l'aide d'un graphique ou d'une table de valeurs, on peut laisser tomber la forme $y=a_1(c_1)^{b(x-h)}$ puisque la forme $y=a_2(c_2)^x$ lui est équivalente.

Par contre, le rôle du paramètre $b$ dans la forme $y=a(c)^{bx}$ prend tout son sens lorsqu'on décrit une situation réelle étant donné qu'il fait référence à la fréquence à laquelle le pourcentage de variation est calculé. 

Voici la preuve algébrique que les équations $y=a_1(c_1)^{b(x-h)}$ et $y=a_2(c_2)^x$ sont parfaitement équivalentes : $$\begin{align} y &= a_1(c_1)^{b(x-h)}\\ &= a_1\left(\color{blue}{(c_1)^{b}}\right)^{x-h} &&\text{car } a^{mn} = (a^m)^{^{\Large n}}\\ &= a_1\, \large{(\color{blue}{c_2})}\normalsize^{x-h} &&\text{en substituant }\color{blue}{(c_1)^{b}} \ \text{par une nouvelle variable : }\large\color{blue}{c_2}\\ &= a_1 \dfrac{(c_2)^{x}}{(c_2)^h} &&\text{car } a^{m-n}=\dfrac{a^m}{a^n}\\ &= \color{red}{\dfrac{a_1}{(c_2)^h}}(c_2)^{x} &&\text{par associativité : }a\times \frac{b}{c}=\dfrac{a}{c} \times b\\ &= \ \ \large \color{red}{a_2}(c_2)^x &&\text{en substituant }\color{red}{\dfrac{a_1}{(c_2)^h}} \ \text{par une nouvelle variable : }\large\color{red}{a_2} \end{align}$$

Par exemple, les fonctions $y=24(2)^{3(x-1)}$ et $y=3(8)^x$ sont parfaitement équivalentes. Voici la preuve : $$\begin{align} y &= 24(2)^{3(x-1)}\\ &= 24\left(2^3\right)^{x-1} &&\text{car } a^{mn} = (a^m)^{^{\Large n}}\\ &= 24(8)^{x-1} &&\text{car } 2^3=8\\ &= 24\dfrac{(8)^x}{(8)^1}&&\text{car } a^{m-n}=\dfrac{a^m}{a^n}\\ &= \dfrac{24}{8}(8)^x &&\text{car }8^1=8\\ &= 3(8)^x &&\text{car } \dfrac{24}{8}=3 \end{align}$$

En conclusion, si on a le graphique de cette fonction, il est beaucoup plus simple de trouver la règle $y=3(8)^x$ que l’autre. En effet, de cette façon, il n’y a que 2 paramètres à déterminer $(a=3$ et $c=8)$ au lieu de 4, soit deux fois moins de travail!

1. Trouver la valeur du paramètre $a$ en substituant les coordonnées de l'ordonnée à l'origine dans l'équation de base $y=a(c)^x$.

2. Trouver la valeur de la base $c$ en utilisant les coordonnées de l'autre point.

Quelle est l'équation de la courbe illustrée ci-dessous?

1. Substituer chacun des points pour créer un système d'équations.

2. Déterminer la valeur de la base $c$ par la méthode de résolution par comparaison.

3. Utiliser un des deux points fournis pour trouver la valeur du paramètre $a.$

Détermine l'équation de la courbe passant par les points $\left(2,\dfrac{-9}{2}\right)$ et $\left(-2,\dfrac{-8}{9}\right).$

Il est plus pratique d'utiliser la forme réduite $(y=a(c)^x+k)$ que d'utiliser la forme canonique $(y=a(c)^{b(x-h)}+k).$ Cette forme s'obtient grâce aux lois des exposants.

Remarque : Toutefois, la valeur du paramètre $a$ de la forme réduite n'est pas égale à celle de la forme canonique. Il en va de même pour la valeur de la base $c$.

1. Remplacer $k$ par la valeur de l'asymptote.

2. Substituer chacun des points pour créer un système d'équations.

3. Déterminer la valeur de la base $c$ à l'aide de la méthode de comparaison.

4. Utiliser un des deux points fournis pour trouver la valeur du paramètre $a.$

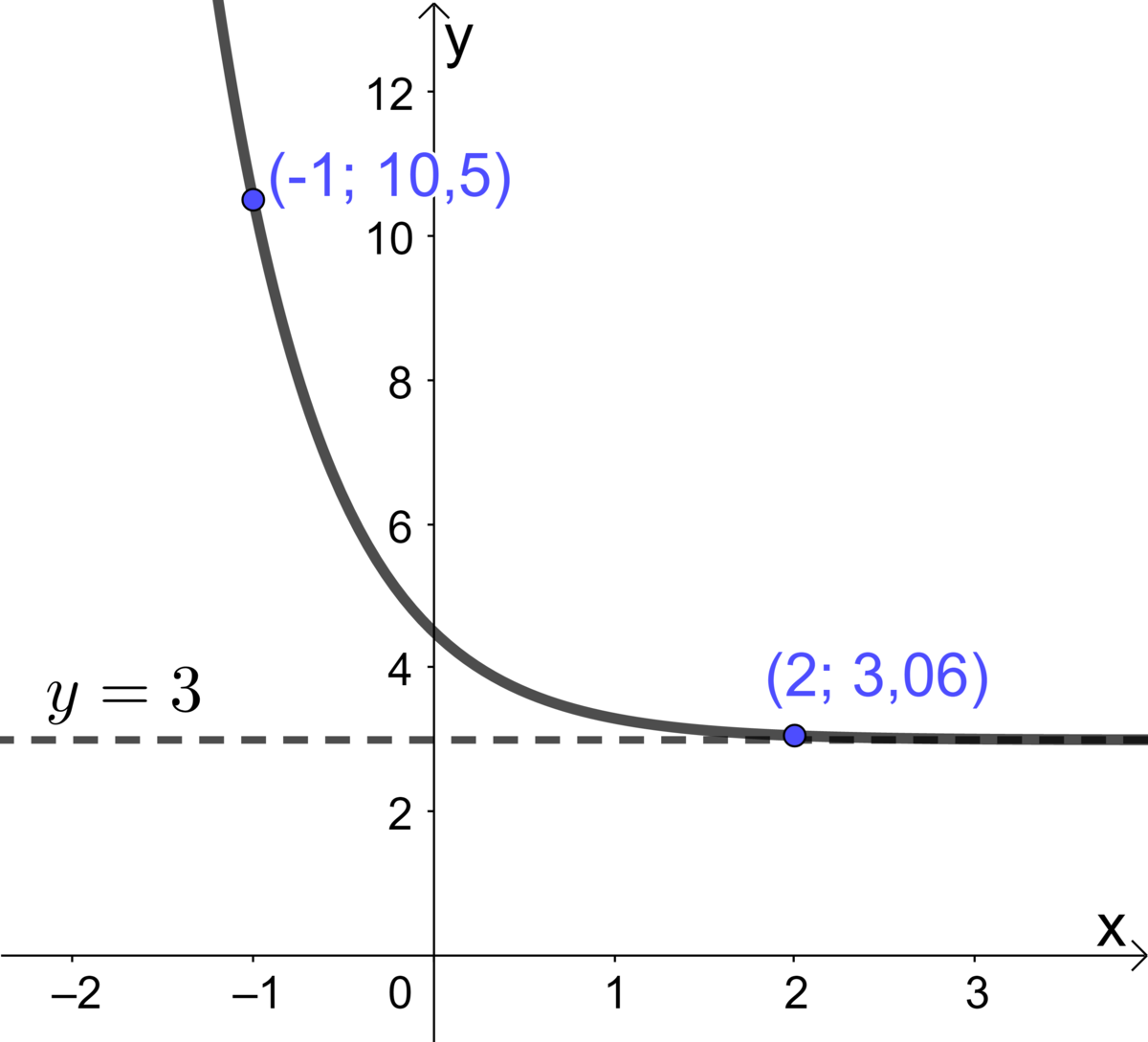
Dans le dernier exemple, on peut appliquer une autre technique de résolution de système d'équations que la méthode de comparaison. Il s'agit d'une méthode de réduction à l'aide de la division. Voici comment il faut procéder :

Lorsqu'on a obtenu les 2 équations $7{,}5=a(c)^{-1}$ et $0{,}06=a(c)^2,$ on peut simplement les diviser comme suit : $$\begin{align} \frac{7{,}5}{0{,}06} &= \frac{a(c)^{-1}}{a(c)^2} \\ 125 &= a^{1-1}(c)^{-1-2}\end{align}$$ Comme $a^{1-1}=a^0=1,$ $a$ disparait. $$\begin{align}125 &=\frac{1}{(c)^3}\\ (c)^3 &= \frac{1}{125}\\ \sqrt[3]{(c)^3} &= \sqrt[3]{\frac{1}{125}} \\ c &= \frac{\sqrt[3]{1}}{\sqrt[3]{125}} = \frac{1}{5} = 0{,}2 \end{align}$$ On obtient évidemment le même résultat avec cette stratégie.

Avec la fonction exponentielle, il y a un facteur multiplicatif entre les variations de la variable dépendante lorsque la variable indépendante augmente de 1. Ce facteur multiplicatif correspond à la base de la fonction.

Voici la table de valeurs de la fonction $y=2(3)^x-1$.

On remarque que le facteur multiplicatif est 3 et ceci correspond à la base $c$ de la fonction exponentielle.

1. Déterminer les variations de la variable dépendante (il faut que celles de la variable indépendante soient de 1) pour déduire le facteur multiplicatif $(c).$

2. Utiliser deux couples $(x,y)$ qu'on remplace dans l'équation $y=a(c)^x+k.$

3. Isoler $k$ dans les deux équations.

4. Résoudre le système d'équations algébriquement pour trouver la valeur du paramètre $a.$

5. Remplacer $a$ dans l'une ou l'autre des deux équations afin de trouver la valeur du paramètre $k.$

6. Écrire l'équation de la fonction exponentielle.

Quelle est l'équation de la fonction exponentielle sous la forme $y=a(c)^x+k$ représentée par la table de valeurs suivante :

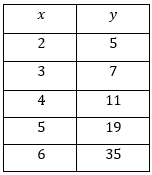
Pourquoi la méthode présentée dans la recherche de la règle d'une fonction exponentielle sous la forme $y=a(c)^x+k$ fonctionne-t-elle?

Voici une preuve intuitive :

Sans perte de généralité, prendre trois couples de points dont les abscisses sont consécutives, tels $(x_1,y_1),(x_2,y_2),(x_3,y_3)$, suffit.

Ainsi : $$\begin{align} y_1 &= a(c)^{x_1}+k \\ y_2 &= a(c)^{x_2}+k \\ y_3 &= a(c)^{x_3}+k \end{align}$$

Il faut calculer les variations de la variable indépendante.  $$\begin{align} y_2-y_1 &= \big(a(c)^{x_2}+k\big)-\big(a(c)^{x_1}+k\big) \\ \Rightarrow\ y_2-y_1 &=a(c)^{x_2}-a(c)^{x_1} \\\\ y_3-y_2 &= \big(a(c)^{x_3}+k\big) - \big(a(c)^{x_2}+k\big) \\ \Rightarrow\ y_3-y_2 &= a(c)^{x_3}-a(c)^{x_2} \end{align}$$

À cette étape, il faut faire une mise en évidence simple dans chaque variation. $$\begin{align} y_2-y_1 &= a\big((c)^{x_2}-(c)^{x_1}\big) \\ y_3-y_2 &= a\big((c)^{x_3}-(c)^{x_2}\big) \end{align}$$

Maintenant, il faut remarquer que $x_2=x_1+1$ et que $x_3=x_2+1$.

Il faut substituer dans les deux variations calculées. $$\begin{align} y_2-y_1 &= a\big((c)^{x_1+1}-(c)^{x_1}\big) \\ y_3-y_2 &= a\big((c)^{x_2+1}-(c)^{x_2}\big) \end{align}$$

Encore une fois, il faut faire une mise en évidence simple dans chaque variation. $$\begin{align} y_2-y_1 &= a(c)^{x_1}\big(c-1\big) \\ y_3-y_2 &= a(c)^{x_2}\big(c-1\big) \end{align}$$

Il ne reste qu'à diviser les deux variations.  $$\displaystyle \frac{y_3-y_2}{y_2-y_1} = \frac{a(c)^{x_2}(c-1)}{a(c)^{x_1}(c-1)}$$

Comme $c \neq 1$ et que $a \neq 0$, alors : $$\displaystyle \frac{y_3-y_2}{y_2-y_1} = \frac{(c)^{x_2}}{(c)^{x_1}} = \frac{(c)^{x_1+1}}{(c)^{x_1}}$$

Or, $\displaystyle \frac{(c)^{x_1+1}}{(c)^{x_1}} = \frac{c}{1}.$

Par conséquent : $$\displaystyle \frac{y_3-y_2}{y_2-y_1} = c$$

C'est ce qui explique pourquoi la variation des valeurs de la variable dépendante, lorsque les abscisses sont consécutives, permet de trouver la base $c$ de la fonction exponentielle sous la forme $y=a(c)^x+k$.