Matières
Niveaux
Dans certaines situations, il peut être utile de passer d'un nombre périodique à une fraction ou l'inverse. La fiche suivante traite des méthodes à utiliser pour effectuer ces passages avec succès.
Avant de présenter ces méthodes, il convient de rappeler la définition de période.
Pour les nombres écrits en notation décimale, une période correspond à un groupe de chiffres qui se répètent sans fin. Lorsqu'on écrit ces nombres, on identifie la première période après la virgule en traçant un trait horizontal au-dessus de celle-ci.
Voici quelques exemples de périodes.||\begin{align} 0{,}666666666...&=0{,}\overline{6}\\
0{,}345252525...&=0{,}34\overline{52}\\
3{,}636363636...&=3{,}\overline{63}\\
0{,}714285714...&=0{,}\overline{714285}\end{align}||
Lorsqu'on tente d'exprimer une fraction en notation décimale en effectuant la division du numérateur par le dénominateur, il se peut que la division ne se termine jamais, créant ainsi une période.
Effectuer la division du numérateur par le dénominateur.
Déterminer la période.
Écrire le nombre en notation décimale en utilisant le trait horizontal au-dessus de la période.
Exprime la fraction |\dfrac{5}{6}| en notation décimale.
Effectuer la division du numérateur par le dénominateur.
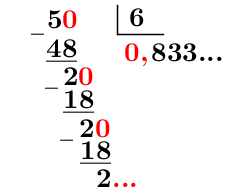
On remarque que le |3| se répète indéfiniment.
Déterminer la période.||0,8\underbrace{\color{blue}{3}}_{\color{blue}{\text{période}}}33...||
Écrire le nombre en notation décimale en utilisant le trait horizontal au-dessus de la période.
On a donc |\dfrac{5}{6}=0{,}8\overline{3}.|
Exprime la fraction |\dfrac{19}{11}| en notation décimale.
Effectuer la division du numérateur par le dénominateur.
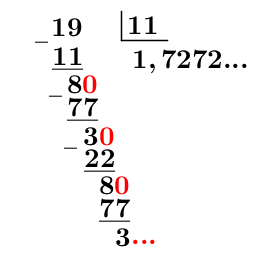
On remarque que le |72| se répète indéfiniment.
Déterminer la période.||1,\underbrace{\color{blue}{72}}_{\color{blue}{\text{période}}}72...||
Écrire le nombre en notation décimale en utilisant le trait horizontal au-dessus de la période.
On a donc |\dfrac{19}{11}=1{,}\overline{72}.|
La méthode pour passer d'un nombre périodique en notation décimale à sa représentation en notation fractionnaire est un peu plus complexe que les autres. Cette méthode fait intervenir l'algèbre.
Définir le nombre périodique comme une variable. Si la période n'est pas collée à droite de la virgule, multiplier par une puissance de |10| pour qu'elle le soit.
Multiplier le nombre périodique par une puissance de |10| pour que la période devienne entière.
Soustraire le nombre de l'étape 1 du nombre de l'étape 2 pour obtenir un entier.
On isole la variable et on simplifie la fraction.
On différenciera deux cas particuliers pour les exemples. Dans un premier cas, la période sera « collée » sur la virgule. Dans un deuxième cas, la période sera séparé de la virgule par au moins un chiffre. La démarche de l'étape 1 sera légèrement différente pour les deux cas.
Exprime |0{,}\overline{36}| en notation fractionnaire
Définir le nombre périodique comme une variable. Si la période n'est pas collée à droite de la virgule, multiplier par une puissance de |10| pour qu'elle le soit. ||n=0{,}\overline{36}||Comme la période est collée à droite de la virgule, on passe à l'étape 2.
Multiplier le nombre périodique par une puissance de |10| pour que la période devienne entière. ||\begin{align}n\times 100&=0{,}\overline{36}\times 100\\ 100n&=36{,}\overline{36}\end{align}||
Soustraire le nombre de l'étape 1 du nombre de l'étape 2 pour obtenir un entier. ||\begin{align}100n-\color{red}{n}&=36{,}\overline{36}-\color{red}{0{,}\overline{36}} & &(\text{La partie décimale s'annule.})\\ 99n&=36\end{align}||
On isole la variable et on simplifie la fraction. ||\begin{align}99n=36\Rightarrow n&=\frac{36}{99}\\ n&=\frac{4}{11}\end{align}||
On a donc |0{,}\overline{36}=\dfrac{4}{11}.|
Exprime |1{,}5\overline{24}| en notation fractionnaire.
Définir le nombre périodique comme une variable. Si la période n'est pas collée à droite de la virgule, multiplier par une puissance de |10| pour qu'elle le soit. ||n=1{,}5\overline{24}||On remarque que la période n'est pas collée sur la virgule.
On devra donc multiplier par |10| pour qu'elle le soit. ||\begin{align}n\times 10&=1{,}5\overline{24}\times 10\\ 10n&=15{,}\overline{24}\end{align}||
Multiplier le nombre périodique par une puissance de |10| pour que la période devienne entière. ||\begin{align}n\times 1\ 000&=1,5\overline{24}\times 1\ 000\\ 1\ 000n&=1\ 524{,}\overline{24}\end{align}||
Soustraire le nombre de l'étape 1 du nombre de l'étape 2 pour obtenir un entier. ||\begin{align}1\ 000n-\color{red}{10n}&=1\ 524{,}\overline{24}-\color{red}{15{,}\overline{24}} & &(\text{La partie décimale s'annule.})\\ 990n&=1\ 509\end{align}||
On isole la variable et on simplifie la fraction. ||\begin{align}990n=1\ 509\Rightarrow n&=\dfrac{1\ 509}{990}\\ n&=\dfrac{503}{330}\end{align}||
On a donc |1{,}5\overline{24}=\dfrac{503}{330}.|
