Matières
Niveaux
En cherchant à recouvrir un solide ou une surface, on fait référence au calcul de son aire. Pour les solides, il y a 3 types d'aire à différencier.
L'aire de la base, généralement notée |A_b,| est la surface occupée par la ou les figures servant de base aux différents solides.
L'aire latérale, généralement notée |A_L,| est la surface occupée par les figures qui ne servent pas de bases aux solides.
L'aire totale, généralement notée |A_T,| est la surface recouverte par toutes les figures formant les différents solides.
Pour savoir laquelle des aires utiliser, il faut se fier au contexte ou lire attentivement les consignes qui sont données dans le problème.
L’aire latérale
Pour réparer une piscine, on veut remplacer la paroi qui la délimite.
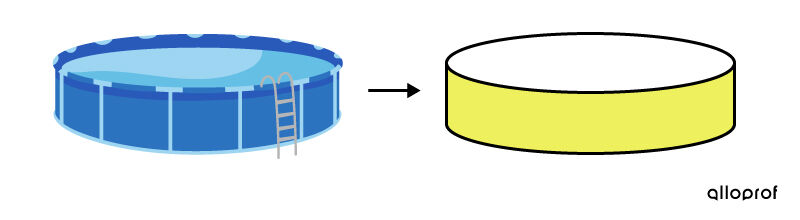
Dans ce contexte, la paroi fait référence à la face latérale du cylindre associé à la piscine. Ainsi, on cible l'aire latérale.
L’aire de la base
Dans un tipi de forme conique, on veut acheter un tapis pour recouvrir le plancher.
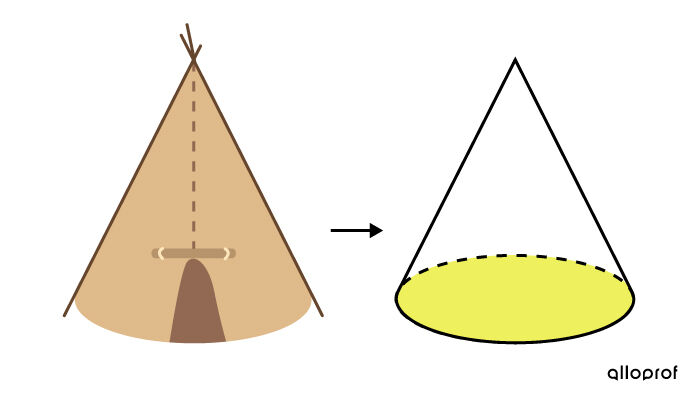
Dans ce cas, le tapis est posé sur le plancher. On fait référence à la base du cône et c'est seulement la superficie de cette figure qui est considérée pour résoudre le problème.
L’aire totale
Pour une occasion spéciale, on offre à un être cher un cadeau qu'on désire emballer afin de préserver la surprise.
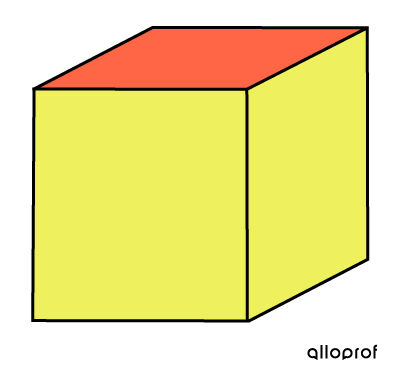
Pour emballer le solide, il faut recouvrir les 4 faces latérales ainsi que les 2 bases. On calcule donc l'aire totale pour résoudre le problème.
Dans tous les cas, l'aire se calcule en |\text{unité}^2| et les unités de mesure utilisées sont, par exemple, des |\text{cm}^2,| des |\text{m}^2| ou des |\text{km}^2.| Lorsqu’on utilise l’exposant 2 dans les unités, on lit « carré », alors |\text{cm}^2| se lit « centimètres carrés ».
Il peut arriver qu'on doive considérer une seule des 2 bases ou seulement une partie des faces latérales. Pour en savoir plus, n'hésite pas à consulter les fiches ci-dessous.
Le volume, généralement noté |V,| est la mesure de l'espace qu'un solide occupe.
Afin de savoir combien de clients pourront recevoir leur commande, une compagnie de distribution d'essence doit savoir quelle quantité, en |\text{m}^3,| son camion-citerne peut contenir.
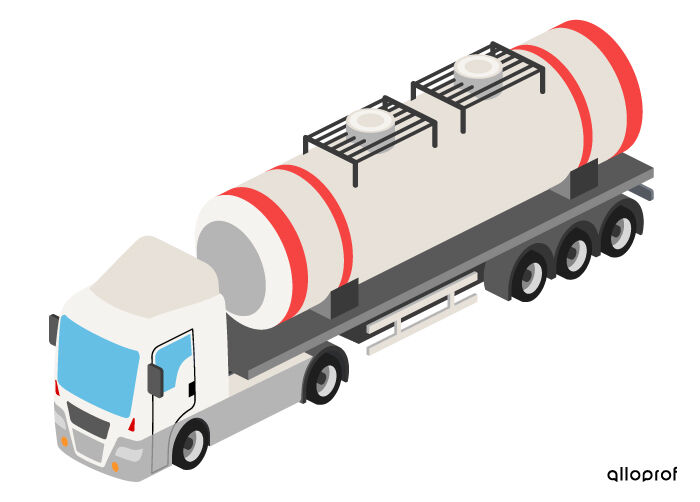
Pour satisfaire leur curiosité, on doit déterminer l'espace en 3 dimensions occupé par la citerne de ce camion. Il est donc question du volume.
Quand on calcule le volume, on peut utiliser 2 types d'unités. Le premier type d’unités fait référence au mètre |(\text{cm}^3, \text{m}^3, \text{dam}^3, …)| et se dit, par exemple, « centimètres cubes ». On peut aussi utiliser les unités de capacité qui font référence au litre |(\text{L}, \text{cL}, \text{mL}, …).| Pour connaitre le lien qui existe entre les deux, n'hésite pas à consulter la fiche sur les unités de capacité et leur conversion.
On peut regrouper les différentes formules pour tous les solides dans le tableau suivant.
| Solide | Formules d'aire | Formule de volume |
|---|---|---|
Cube |
|\begin{align}A_b &= \ \color{#3a9a38}{c}^2\\\\ A_L &= 4 \color{#3a9a38}{c}^2\\\\ A_T &= 6 \color{#3a9a38}{c}^2 \end{align}| |
|V = \color{#3a9a38}{c}^3| |
Prisme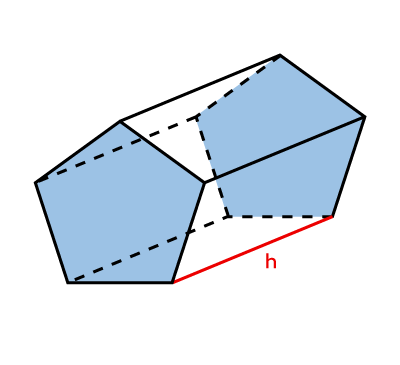 |
|\begin{align} \color{#3b87cd}{A_b} &= \text{formule associée à la figure} \\\\ A_L &= \color{#3b87cd}{P_b} \times \color{#ec0000}{h} \\\\ A_T &= A_L + 2 \color{#3b87cd}{A_b} \end{align}| |
|V = \color{#3b87cd}{A_b} \times \color{#ec0000}h| |
| Pyramide  |
|\begin{align} \color{#3b87cd}{A_b} &= \text{formule associée à la figure} \\\\ A_L &= \dfrac{\color{#3b87cd}{P_b} \times \color{#fa7921}{a}}{2} \\\\ A_T &= A_L + \color{#3b87cd}{A_b} \end{align}| | |V = \dfrac{\color{#3b87cd}{A_b} \times \color{#ec0000}{h}}{3}| |
Sphère ou boule |
Aire de la sphère |A_T = 4 \pi \color{#3a9a38}{r}^2| |
Volume de la boule |V= \dfrac{4 \pi \color{#3a9a38}{r}^3}{3}| |
Cylindre |
|\begin{align} \color{#3b87cd}{A_b} &= \pi \color{#3a9a38}{r}^2 \\\\ A_L &= 2 \pi \color{#3a9a38}{r} \color{#ec0000}h \\\\ A_T &= A_L + 2 \color{#3b87cd}{A_b} \end{align}| |
|V = \color{#3b87cd}{A_b} \times \color{#ec0000}h| |
Cône |
|\begin{align} \color{#3b87cd}{A_b} &= \pi \color{#3a9a38}r^2 \\\\ A_L &= \pi \color{#3a9a38}r \color{#fa7921}a \\\\ A_T &= A_L + \color{#3b87cd}{A_b} \end{align}| |
|V = \dfrac{\color{#3b87cd}{A_b} \times \color{#ec0000}h}{3}| |
La ou les bases des prismes et celle des pyramides peuvent prendre différentes formes. Pour t’aider à calculer leur aire, n’hésite pas à consulter le tableau résumé des formules d’aire des figures planes.
Pour valider ta compréhension de façon interactive à propos de l'utilisation des formules d'aire et de volume des solides dans le but de trouver une mesure manquante, consulte la MiniRécup suivante.
