Matières
Niveaux
Les relations métriques dans le triangle rectangle
Fiche | Mathématiques
Secondaire
4-5
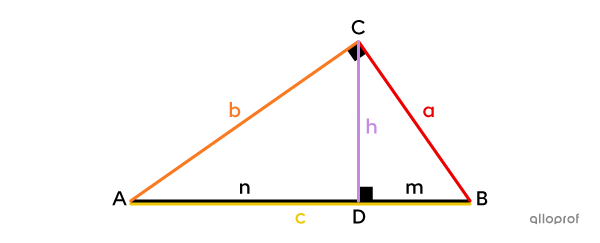
Dans un triangle rectangle, si on trace la hauteur |\boldsymbol{(h)}| issue de l’angle droit, on crée 2 autres triangles rectangles. On peut déduire que ces 3 triangles sont semblables entre eux par la condition minimale A-A.
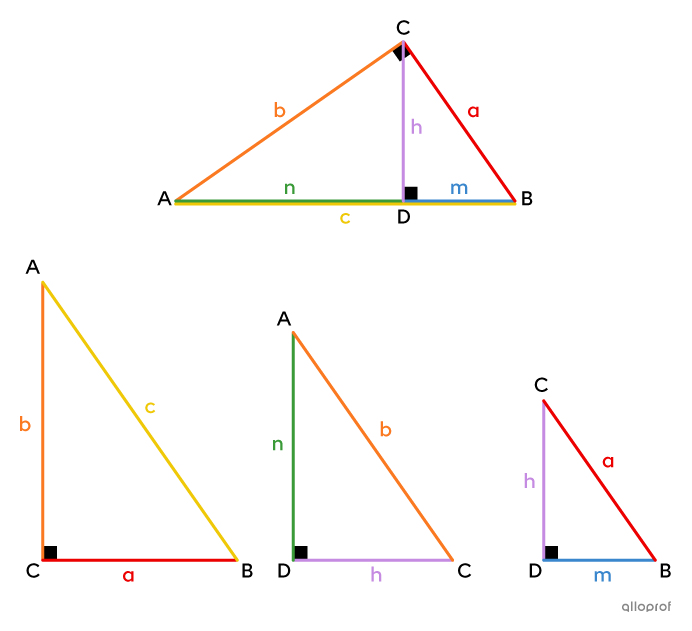
Il est possible d'établir plusieurs proportions à partir des côtés homologues de ces triangles rectangles. Ces proportions permettent d'énoncer 3 relations métriques qui facilitent la recherche de mesures manquantes dans un triangle rectangle.
||\begin{align}\dfrac{\color{#3b87cd}m}{\color{#ec0000}a}&=\dfrac{\color{#EC0000}a}{\color{#efc807}c}\\\\
\dfrac{\color{#3a9a38}n}{\color{#fa7921}b}&=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\end{align}||
Le théorème de la hauteur relative à l'hypoténuse
||\dfrac{\color{#3b87cd}m}{\color{#c58ae1}h}=\dfrac{\color{#c58ae1}h}{\color{#3a9a38}n}||
Le théorème du produit des cathètes
||\dfrac{\color{#c58ae1}h}{\color{#ec0000}a}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}||
Voici les étapes à suivre pour déterminer la mesure d’un segment dans un triangle à l’aide des relations métriques.
-
Identifier les mesures données et celle qu’on cherche.
-
Déterminer la relation métrique à utiliser.
-
Déterminer la mesure manquante.
S’il manque plus d’une mesure pour utiliser une relation métrique, on peut parfois les trouver à l’aide du théorème de Pythagore.
Le théorème de la cathète
Dans un triangle rectangle, chaque cathète |(a| et |b)| est moyenne proportionnelle entre sa projection sur l’hypoténuse |(m| ou |n)| et l’hypoténuse entière |(c).|
|\dfrac{\color{#3b87cd}m}{\color{#ec0000}a}=\dfrac{\color{#ec0000}a}{\color{#efc807}c}\ \Rightarrow\ \color{#ec0000}a^2= \color{#3b87cd}m\color{#efc807}c|
|\dfrac{\color{#3a9a38}n}{\color{#fa7921}b}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\ \Rightarrow\ \color{#fa7921}b^2=\color{#3a9a38}n\color{#efc807}c|
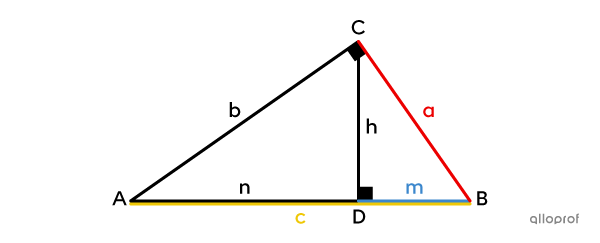
Détermine la mesure de |\overline{BC}| dans le triangle suivant.
-
Identifier les mesures données et celle qu’on cherche
||\begin{align}\text{m}\overline{AB}&=c=16\ \text{cm}\\\text{m}\overline{BD}&=m=4\ \text{cm}\\\text{m}\overline{BC}&=a=\ ?\end{align}|| -
Déterminer la relation métrique à utiliser
On cherche la relation métrique qui fait intervenir |a,| |c| et |m.| Il s’agit du théorème des cathètes. -
Déterminer la mesure manquante
||\begin{align}a^2 &= m c \\a^2 &= 4\times 16\\a^2 &= 64\\a &= 8\end{align}||
Réponse : La mesure de |\overline{BC}| est de |8\ \text{cm}.|
Le théorème de la hauteur relative à l'hypoténuse
Dans un triangle rectangle, la hauteur issue de l’angle droit |(h)| est moyenne proportionnelle entre les 2 segments qu’elle détermine sur l’hypoténuse |(m| et |n).|
|\dfrac{\color{#3b87cd}m}{\color{#c58ae1}h}=\dfrac{\color{#c58ae1}h}{\color{#3a9a38}n}\ \Rightarrow\ \color{#c58ae1}h^2 = \color{#3b87cd}m\color{#3a9a38}n|
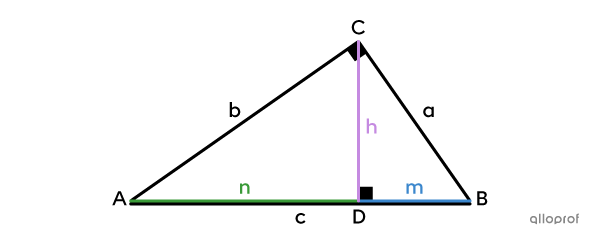
Détermine la mesure de |\overline{BD}| dans le triangle suivant.
-
Identifier les mesures données et celle qu’on cherche
||\begin{align}\text{m}\overline{AD}&=n=12\ \text{cm}\\\text{m}\overline{CD}&=h=6\ \text{cm}\\\text{m}\overline{BD}&=m=\ ?\end{align}|| -
Déterminer la relation métrique à utiliser
On cherche la relation métrique qui fait intervenir |h,| |m| et |n.| Il s’agit du théorème de la hauteur relative à l’hypoténuse. -
Déterminer la mesure manquante
||\begin{align}h^2 &= mn\\6^2 &= 12\times m\\36 &= 12\times m\\3 &= m\end{align}||
Réponse : La mesure de |\overline{BD}| est de |3\ \text{cm}.|
Le théorème du produit des cathètes
Dans un triangle rectangle, le produit de l’hypoténuse |(c)| et de la hauteur correspondante |(h)| est égal au produit des cathètes |(a| et |b).|
|\dfrac{\color{#c58ae1}h}{\color{#ec0000}a}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\ \Rightarrow\ \color{#efc807}c\color{#c58ae1}h = \color{#ec0000}a\color{#fa7921}b|
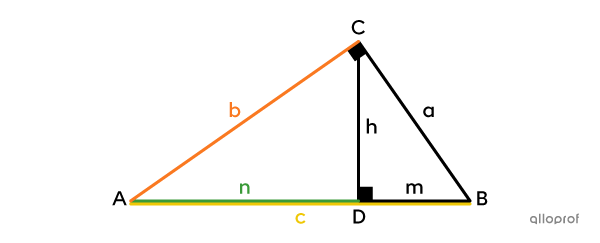
Détermine la mesure de |\overline{CD}| dans le triangle suivant.
-
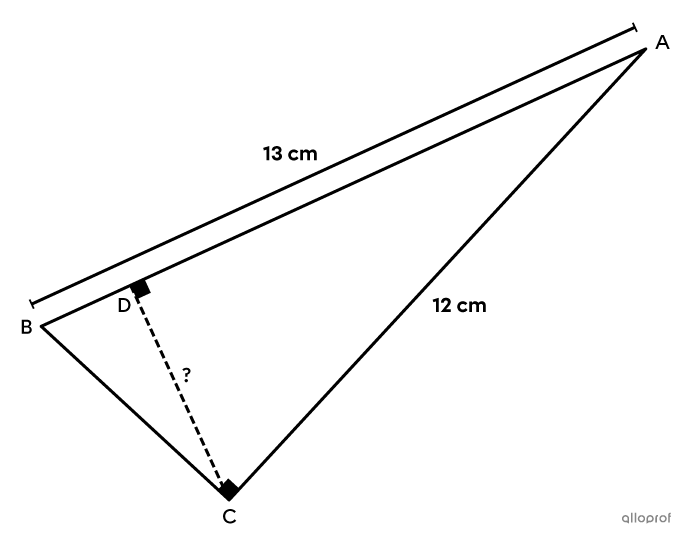
Identifier les mesures données et celle qu’on cherche
||\begin{align}\text{m}\overline{AB}&=c=13\ \text{cm}\\\text{m}\overline{AC}&=b=12\ \text{cm}\\\text{m}\overline{CD}&=h=\ ?\end{align}|| -
Déterminer la relation métrique à utiliser
Il n’y a pas de relation métrique qui fait intervenir ces 3 grandeurs seulement. Par contre, pour utiliser le théorème du produit des cathètes, il ne manque que la mesure de la 2e cathète |(\overline{BC}),| qu’on peut déterminer à l’aide du théorème de Pythagore.||\begin{align} a^2 + b^2 &= c^2\\a^2 + 12^2 &= 13^2\\a^2 &= 169 - 144\\a^2 &= 25\\a &= 5\end{align}|| -
Déterminer la mesure manquante
||\begin{align}ch&=ab\\13h &= 5\times 12\\13h &= 60\\h &\approx 4{,}6\end{align}||
Réponse : La mesure de |\overline{CD}| est d’environ |4{,}6\ \text{cm}.|
La résolution de problème impliquant les relations métriques
Il est possible de résoudre des problèmes plus complexes en utilisant plusieurs relations métriques.
Dans l’image ci-dessous, la mesure du segment |\overline{BC}| est |100\ \text{cm},| alors que celle du segment |\overline{AC}| est de |116{,}62\ \text{cm}.| Détermine la mesure du segment |\overline{DE}.|
Voir la solution
Pour valider ta compréhension à propos des démonstrations de façon interactive, consulte la MiniRécup suivante.
