Bonjour, Je cherche à comprendre pourquoi dans cette formule, la division est 2 et l'exposant au final 11 et pouvez vous me donner un autre exemple pour que je puisse mieux comprendre. Merci!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
et pourquoi plus loin dans la vidéo. Il explique que la racine carré de 9 est 3 à cause que le 9 et une demi devient un exposant fractionnaire.
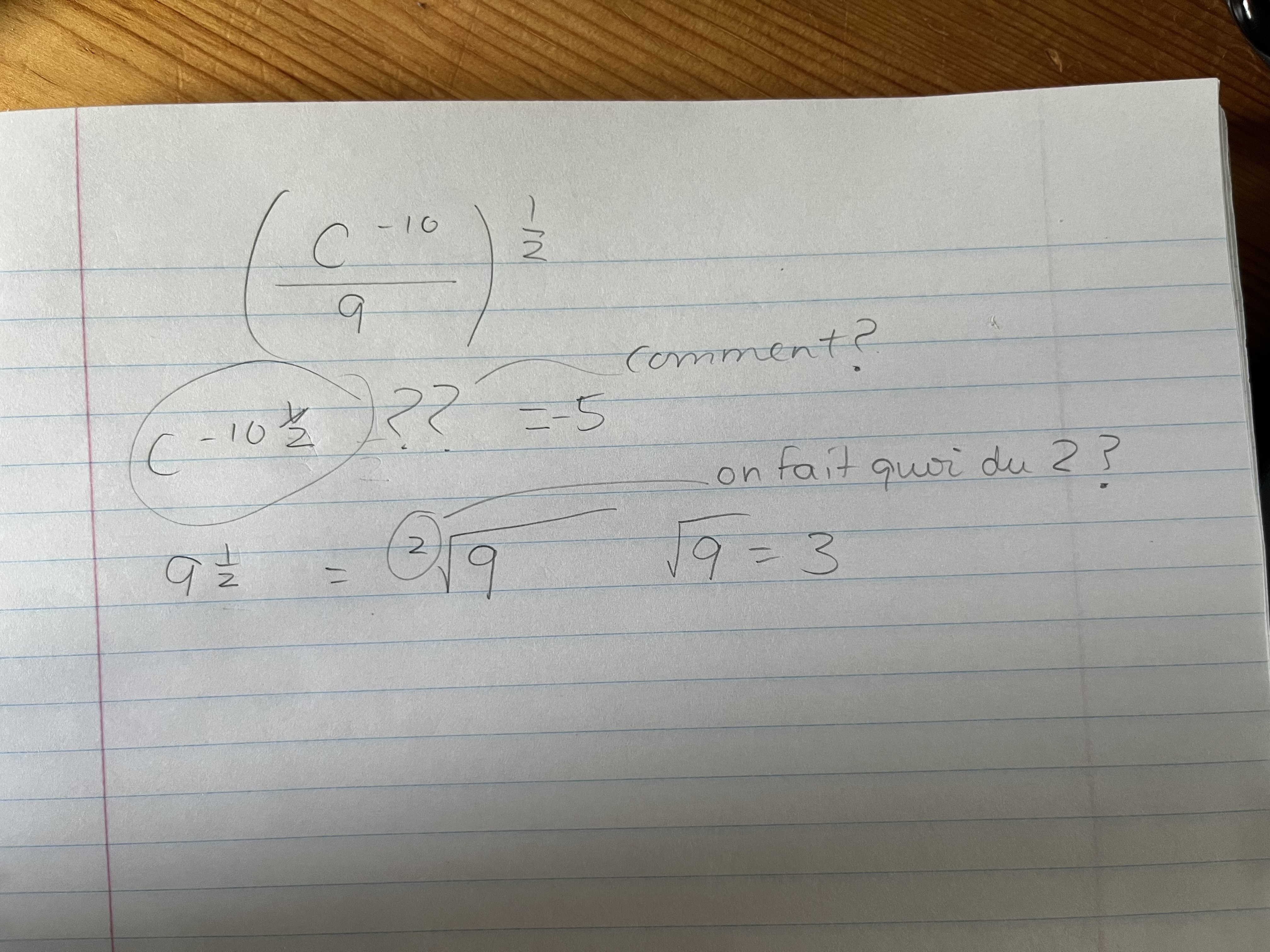
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.




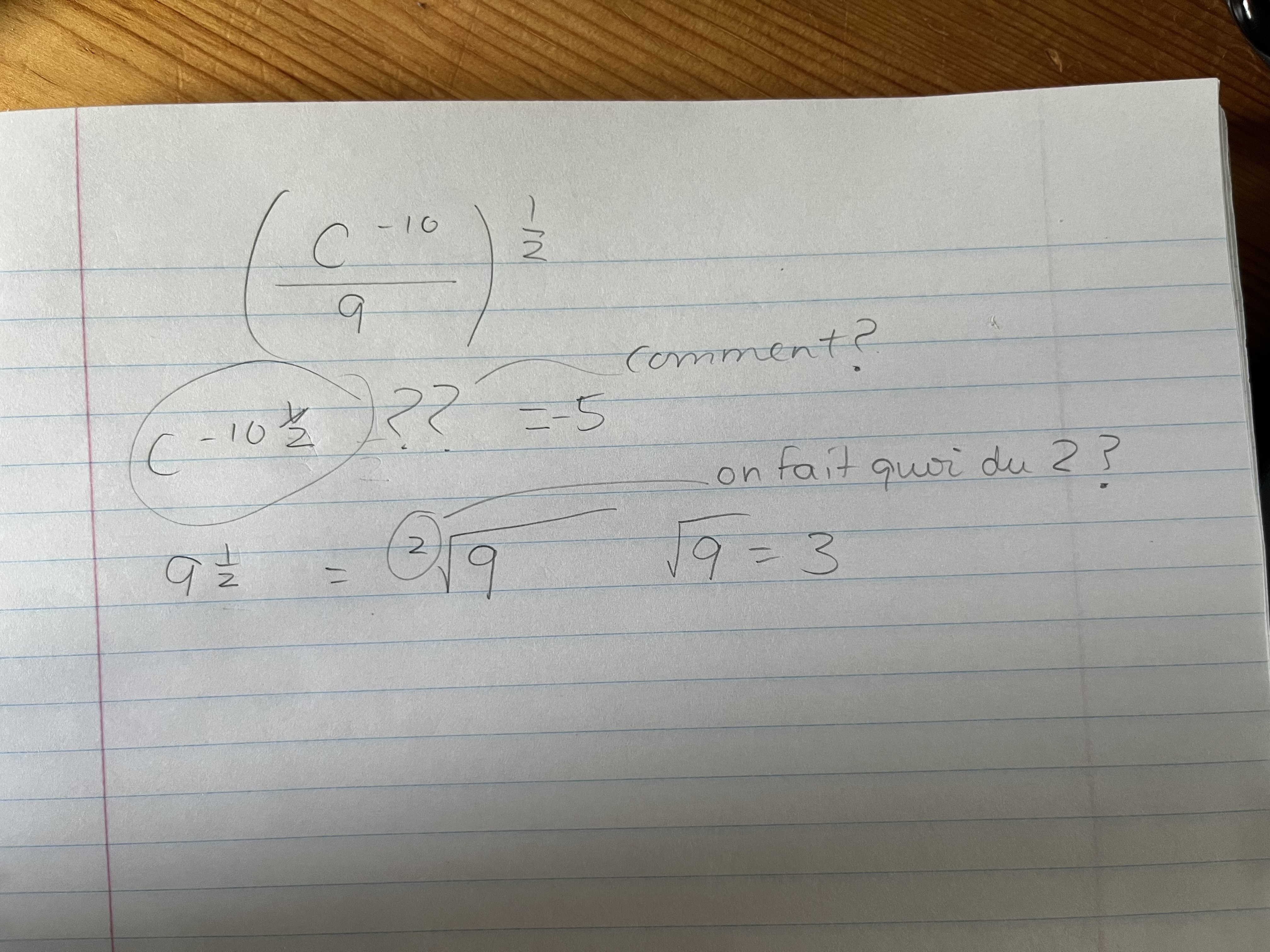






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Ici :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
La racine carrée peut se réécrire en exposant fractionnaire 1/2 grâce à cette loi des exposants :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
On a donc :
$$ \sqrt{81c^{22}}$$
$$ (81c^{22})^{ \frac{1}{2} }$$
L'exposant se distribue sur chaque facteur :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
$$ (81)^{\frac{1}{2}}(c^{22})^{\frac{1}{2}}$$
La racine carrée de 81 est 9 :
$$ 9(c^{22})^{\frac{1}{2}}$$
Puis, on peut multiplier les exposants 22 et 0,5 selon cette loi des exposants :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce qui nous donne un exposant de 11, car \(22 \times \frac{1}{2}=11\):
$$ 9c^{11}$$
En ce qui concerne ta seconde question, tu dois appliquer les lois des exposants encore une fois.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ici, tu as l'exposant -10 × ½. Le résultat de cette multiplication est -5, donc :
$$ c^{-10 × \frac{1}{2}} = c^{-5}$$
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Une racine carrée peut s'écrire comme ceci \( \sqrt{}\) ou comme ceci \( \sqrt[2]{}\), c'est la même chose! ;) Il faut écrire l'indice lorsqu'il est différent de 2 seulement, donc lorsqu'on a une racine cubique, une racine quatrième, une racine cinquième, etc.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voilà! J'espère que c'est plus clair pour toi! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!