Populaires
Re : Question
Bonjour à toi!
Merci pour ta question :)
Pour faire un diagramme circulaire, tu dois connaître la valeur de chacune des parties qui composera ton diagramme circulaire. Ensuite, tu devras utiliser les proportions pour remettre la valeur d'une certaine partie sur 360, étant donné qu'un cercle fait 360°.
Par exemple, si 1/4 des élèves d'une classe jouent au soccer, il faudrait trouver que la portion du cercle à identifier pour le soccer serait de 90°/360°.
Pour tracer le diagramme circulaire, tu as besoin d'un compas et d'un rapporteur d'angle. Le compas te servira à tracer le cercle et le rapporteur d'angle, à tracer de façon précise les parties de ton diagramme circulaire.
Je te laisse une fiche qui explique le diagramme circulaire juste ici:
J'espère que ma réponse t'aura aidé!
Bonne journée :)
Ariane
Re : Question
Bonjour DiamantRose7100!
Merci pour ton intérêt pour la Zone d'Entraide! :)
Je transmets le message à l'équipe qui pourront te contacter :)
Bonne journée!
Question
Bonjour,j'aimerais savoir quand on dit :
Est-ce que les actions de Marylin sont justifiés?
Est-ce que voudrait dire si ces actions valaient la peine?
Parce même avec le dictionnaire,je n'arrive pas à comprendre le terme justifié.
Merci beaucoup pour votre collaboration!
Re : Question
Bonjours pour répondre a ta question il faut que tu trouve la mesure des angles demandé
par example tu peut déja écrire que l'angle A et B son de 90
et tu peut déja aussi faire le triangle en sachant qu'il est équilatéral et que la somme total des angles d'un triangle sont de 180 degré
et il y a une formule pour calculer la somme des angle complet d'un polygone ;
Re : Question
Bonjour AigleOmicron4094,
Pour trouver l'infinitif d'un verbe conjugué, il faut connaître les terminaisons du verbe à l'indicatif présent, à l'imparfait et/ou au futur simple.
Par exemple, les verbes terminant par e - es - e - ons - ez - ent à l'indicatif présent sont des verbes qui terminent en -er à l'infinitif.
J'espère que ça t'a aidé ! :)
Noémie
Re : Question
A l'infinitif, le verbe finit en « er », « ir », « oir » ou « re » et ne change ni avec le temps, ni avec les personnes. Pour chaque verbe, il n'y a qu'un seul infinitif.
Re : Question
Salut !
La question manque un peu de contexte. Cela va dépendre des informations que tu as à ta disposition. Voici une fiche qui pourrait t'aider à comprendre comment trouver les paramètres de cette fonction incluant a :
Ce paramètre correspond à la hauteur entre deux segments. Si la valeurs est de 1/2 (0,5), alors le saut d'un segment à l'autre est de 1/2.
Si tu as d'autres questions, n'hésite pas !
Re : Question
Bonsoir,
Ta question nous inquiète beaucoup! Nous espérons que tu vas bien et nous espérons aussi que tu vas aller chercher de l'aide!
Sache aussi que les spécialistes de Tel-Jeunes sont les meilleures personnes pour t'aider si tu vis des moments difficiles. N'hésite surtout pas à te tourner vers eux! Pour les contacter, tu peux suivre ce lien : https://www.teljeunes.com/Accueil
Ceci étant dit, n'hésite pas à nous recontacter si tu veux nous partager plus d'informations. Prends soin de toi!
Re : Question
Bonjour CigaleOrange,
Merci pour ta question!
Que veux-tu dire par 75 N de cuivre? S'agit-il de son poids (force gravitationnelle)? Dans ce cas, s'il flotte, la force de flottabilité exercée sur lui est la même que la force gravitationnelle qu'il subit, soit 75 N.
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re : Question
Merci pour ta question!
En fait, tu étais proche de la bonne réponse! Tu as seulement oublié d'inclure la force gravitationnelle pour équilibrer le tout...
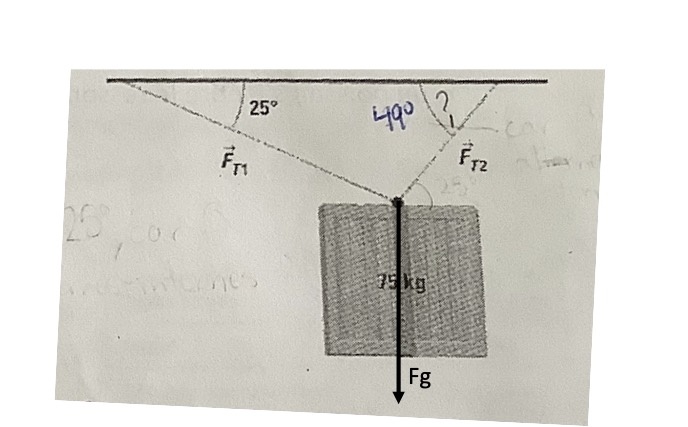
Commençons par faire un schéma de la situation en incluant toutes les forces, c'est-à-dire, FT1, FT2 et Fg :
En refaisant tes calculs, en incluant la force gravitationnelle on trouve que :
$$ \Sigma_F = F_{T1y} + F_{T2y} +F_{gy} = 0 $$
$$ \Sigma_F = 500sin(25°) +F_{T2y} -75•9,81 = 0 $$
$$ F_{T2y} = F_{T2}•sin(\theta) = 524,44\:N $$
Cependant, il nous reste à résoudre une équation à deux inconnus... C'est pourquoi on fait intervenir la somme des forces horizontales :
$$ \Sigma_F = F_{T1x} + F_{T2x} = 0 $$
$$ \Sigma_F = 500•cos(25°) + F_{T2}•cos(\theta) = 0 $$
On peut donc isoler FT2 dans les deux équations... :
$$ F_{T2}•sin(\theta) = 524,44\:N $$
$$ F_{T2}• = \frac{524,44\:N }{sin(\theta)} $$
et
$$ 500•cos(25°) + F_{T2}•cos(\theta) = 0 $$
$$ F_{T2} = \frac{-500•cos(25°)}{cos(\theta)} $$
...pour ensuite les comparer :
$$ \frac{524,44\:N }{sin(\theta)} = \frac{-500•cos(25°)}{cos(\theta)} $$
$$ \frac{sin(\theta)}{524,44\:N} = \frac{cos(\theta)}{-500•cos(25°)} $$
$$ \frac{sin(\theta)}{cos(\theta)} = \frac{524,44\:N}{-500•cos(25°)} $$
$$ tan(\theta) = \frac{524,44\:N}{-500•cos(25°)} $$
$$ tan(\theta) = -1,1573... $$
$$ \theta = arctan(-1,1573...) = -49° $$
Voilà!