Populaires
Re : Question
☺
Je préfère utiliser la forme générale f(x) = ax²+bx+c
Le système d équations me semble plus facile à résoudre surtout quand la valeur initiale est connue car f(0) = c.
Ainsi on a f(x) = ax²+bx+6 .
f(4) = 54
a·4²+b·4+6 = 54
16a+4b = 48 est ta première équation, qu on peut simplifier à 4a+b = 12.
Tu fais pareil avec f(5) = 76 et tu trouves la deuxième équation.
Tu résous le système.
Le sommet est le point (-b/2a, f(-b/2a)).
Re : Question
Comme Madame Katia a expliqué, tu utilises les 3 points donnés f(0)=6, f(4)=54 et f(5)=76 dans l'équation
f(x) = a(x - h)² + k
tu as donc 6 = a(0 - h)² + k c'est-à dire 6 = ah² + k (1)
54 = a(4 - h)² + k (2)
76 = a(5 - h)² + k (3)
en remplaçant k par 6 - ah² ( obtenu de (1) ) dans les équations (2) et (3) tu peux déterminer a et h puis finalement k
Connaissant l'équation de la parabole tu pourras facilement déterminer le minimum.
Question
Bonjour, je ne comprend pas comment faire cette exercice:
Pouvez-vous m'aider s'il vous plait?
Merci
Re : Question
Salut !
Il ne s'agit pas d'une matière couverte par Alloprof puisqu'elle est plus avancée. Toutefois, l'exercice fait en effet référence à l'effet Doppler.
Ton explication semble aussi correct.
Si tu as d'autres questions, n'hésite pas !
Re : Question
Salut CobaltDynamique4315,
Merci pour ta question,
Selon mes recherches, le nom exact de la liaison dans l'Acétyle-CoA est thioester,
J'espere que cela t'auras aidé, n'hésite pas a nous réécrire si tu as d'autres questions!
- OpaleOptimiste1657
Question
Petite idée simple pour amélioré votre site internet: Plusieurs personnes comme moi font des devoirs tard le soir, l'ennui est le suivant: Le site est presque entrièrement blanc! Cela fait un peut mal au yeux alors je propose de rajouter un mode sombre pour que le blanc devienne du noir au gris.
Re : Question
☺
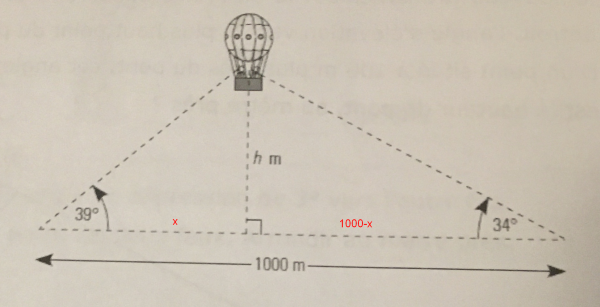
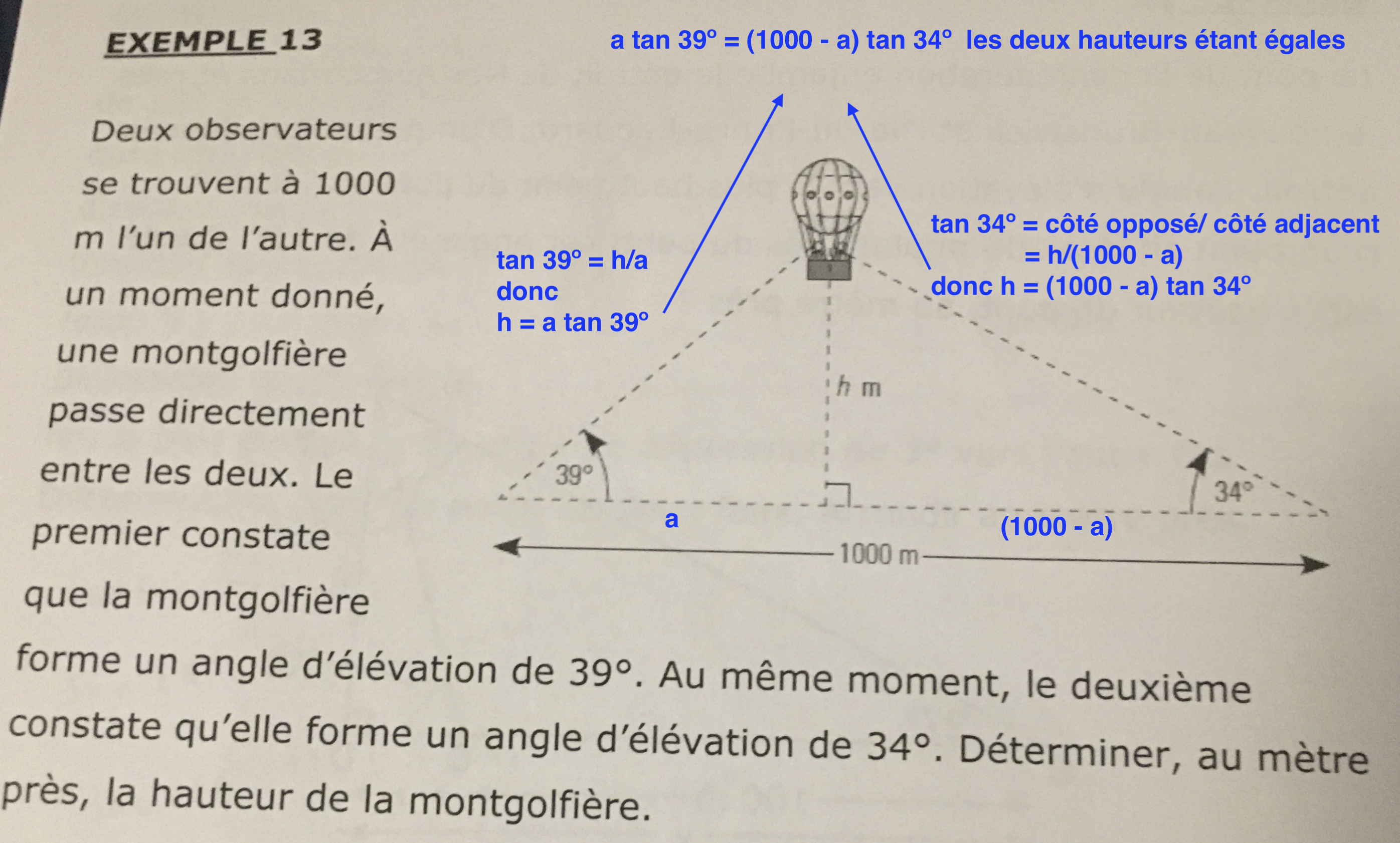
Avec tangente dans les deux triangles rectangles, tu résous le système d équations suivant:
tan39° = .../...
tan34° = .../...
Re : Question
Salut !
Pour cette exercice, il te faudra utiliser la loi des cosinus. Et voici justement une fiche sur le sujet qui te montrera la marche à suivre :
Tu pourras ainsi trouver l'angle à la montgolfière. À partir de là, tu peux utiliser la loi des sinus pour trouver la distance entre un des deux observateurs et la montgolfière :
Finalement, tu pourras utiliser les relations trigonométriques pour trouver la valeur de la hauteur !
Je te laisse essayer de résoudre l'exercice par toi-même et si tu as d'autres questions, n'hésite pas !