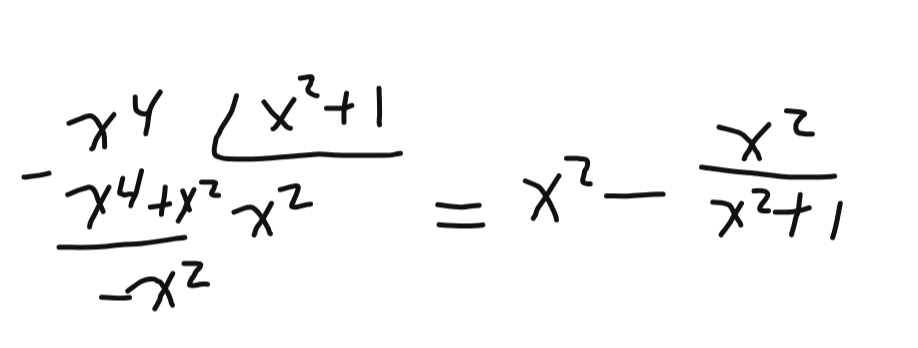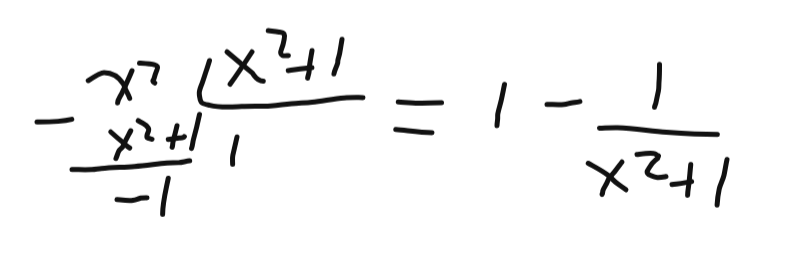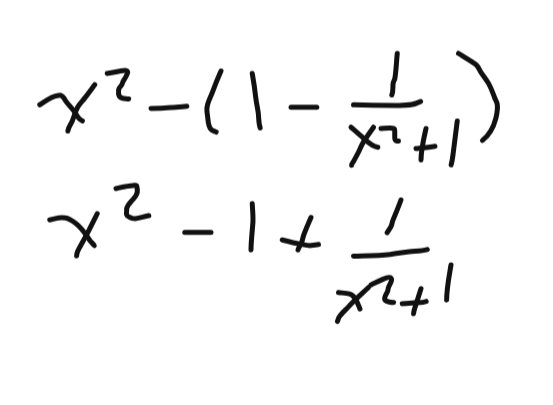Populaires
Re : Question
Salut,
Merci d'utiliser la zone d'entraide.
Une phrase a toujours 4 formes.
- Positive ou négative. Exemples : J'aime les fruits (positive) - Je n'aime pas les fruits (négative)
- Active ou passive. Exemples : Julie a fait un gâteau (active) - Le gâteau a été fait par Julie (passive)
- Neutre ou emphatique. Exemples : Faire du sport est bon pour la santé (neutre) - C'est faire du sport qui est bon pour la santé (emphatique)
- Personnelle ou impersonnelle. Exemples : Colin donne des craquelins aux élèves (personnelle) - Il y a des craquelins de disponibles pour les élèves (impersonnelle)
Voici les pages que tu peux consulter pour en apprendre plus sur les formes de phrase.
La phrase de base:
La phrase négative:
La phrase passive:
La phrase emphatique:
La phrase impersonnelle:
Pour ta deuxième question, je suis moins certaine de bien comprendre puisque la proposition est un concept de grammaire traditionnelle qui n'est plus utilisé aujourd'hui.
On disait qu'il y avait une proposition par verbe. Donc, dans une phrase avec deux verbes, on parle de deux propositions.
Aujourd'hui, on parlera plutôt de subordonnées. Il y a donc une phrase enchâssante et des phrases enchâssées. Les subordonnées sont des phrases à l'intérieure de la phrase enchâssante.
N'hésite pas à revenir nous voir en spécifiant tes incompréhensions pour que nous puissions t'aider davantage.
À bientôt,
Karen
Question
je voulez savoir comment sa marche fin lapin 3 et pourquoi il a seulement 5 niveaux de ils
Re : Question
Salut AnkylosaureJuste378 😁
Merci pour ta question!
Pour l'intégration, mes notions sont loin (on a certainement un.e membre de l'équipe qui pourra t'aider si tu souhaites reposer ta question ultérieurement).
Cependant, je peux te montrer comment faire la division polynomiale au cas où ça te soit utile pour faire une somme d'intégrales (ça existe, non?).
Voici la démarche. On commence par diviser x^4 par (x^2+1).
Ensuite, on peut poursuivre la division. Avec, x^2 par (x^2+1).
L'expression finale sera la suivante.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re : Question
Bonjour!
Pour factoriser cette expression, on peut utiliser la technique du produit-somme :
$$\frac{2t^2 - t - 1}{t^2 - 3t + 2}$$
Au numérateur \(2t^2 - t - 1\), on cherche deux nombres dont la somme est de -1 et dont le produit est de 2×-1=-2. Ces deux nombres sont 1 et -2, car 1+-2=-1 et 1×-2=-2 :
$$\frac{2t^2 +t-2t - 1}{t^2 - 3t + 2}$$
Au dénominateur \(t^2 - 3t + 2\), on cherche deux nombres dont la somme est de -3 et dont le produit est de 1×2=2. Ces deux nombres sont -1 et -2, car -1+-2=-3 et -1×-2=2 :
$$\frac{2t^2 +t-2t - 1}{t^2 -t-2t + 2}$$
Ensuite, on effectue une mise en évidence double au numérateur :
$$\frac{t(2t +1)-(2t + 1)}{t^2 -t-2t + 2}$$
et au dénominateur :
$$\frac{t(2t +1)-(2t + 1)}{t(t -1)-2(t - 1)}$$
Au numérateur, on peut faire une mise en évidence simple du facteur (2t+1) :
$$\frac{(2t +1)(t-1)}{t(t -1)-2(t - 1)}$$
Et au dénominateur, on factorise (t-1) :
$$\frac{(2t +1)(t-1)}{(t -1)(t-2)}$$
Finalement, on élimine le facteur (t-1) qui se retrouve au numérateur et au dénominateur :
$$\frac{(2t +1)}{(t-2)}$$
Voilà! :)
J'espère que c'est plus clair pour vous!
Re : Question
Bonjour!
Une quête identitaire, c'est lorsqu'on entreprend une quête afin d'apprendre à se connaitre et de définir notre identité. Cette quête peut prendre plusieurs formes.
Par exemple, une personne peut tenter de retracer ses ancêtres et de créer un arbre familial.
Une autre personne peut vouloir apprendre à se connaitre en voyageant et en découvrant le monde! :D
J'espère t'avoir aidé! Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re : Question
Bonjour!
Oui! Il est préférable de choisir les sciences ST afin de pouvoir accéder aux études pour ces professions. :D
Laurie :)
Re : Question
Bonjour!
Non, la Terre n'était pas rouge. Elle était, au départ (il y a très très longtemps) couverte de roche. Elle a graduellement pris l'apparence qu'elle a aujourd'hui. :)
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir! :D
Laurie :)
Re : Question
Bonjour LoupSigma,
Pour ma part, j'ai été en secondaire 4 en CST, puisque mes notes me l'obligeaient. Par conséquent, aller en CST m'a ouvert la porte à de grands résultats ! Allant de 60 % en secondaire 3 à 96 % en secondaire 4 !
CST est un grand avantage, puisque tu vois la matière plus lentement et puis, si tu peux faire ton TS de 4 en secondaire 5, cela est très pratique puisqu'il y a plein de choses que tu auras déjà vu. J'ai fait TS4 en secondaire 5. Mais tout dépend des écoles.
Pour ce qui est des maths SN, ce que j'en ai entendu, c'est que c'était assez difficile. Mes amis, qui étaient très bons en mathématiques, avaient de la difficulté. Comme tu m'as l'air de ne pas vraiment aimer les mathématiques, je ne te suggère pas d'aller en SN puisque la charge de travail sera encore plus grande et les théories mathématiques sont assez complexes.
De plus, tout dépend de ce que ton programme au cégep requière. Certains programmes obligent à avoir SN ou TS.
Voici une fiche pour t'aider. Je te suggère d'y jeter un coup d'œil sur les différentes théories que tu verras en SN et CST.
N'hésite pas si tu as d'autres questions !
BrachiosaureTimide314
Re : Question
Bonjour!
Je ne suis pas certaine de comprendre ta question.
Les causes viennent effectivement toujours avant les conséquences. Cependant, une conséquence peut être la cause d'une autre conséquence.
Exemple :
Je n'ai pas porté de manteau (cause) -> donc je suis malade (conséquence)
Je suis malade (cause) -> donc j'ai manqué l'école (conséqence)
Il peut y avoir un enchaînement de causes et de conséquences.
De plus, une cause peut entrainer plusieurs conséquences.
De la même façon, un évènement peut avoir plusieurs causes.
J'espère t'avoir aidé à comprendre! Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re : Question
Bonjour!
Je te suggère de consulter la réponse que l'élève a obtenue à sa question similaire à la tienne! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)