Secondaire 4 • 3a
Salut
J'ai une question à propos de comment traduire un demi-plan par une inéquation.
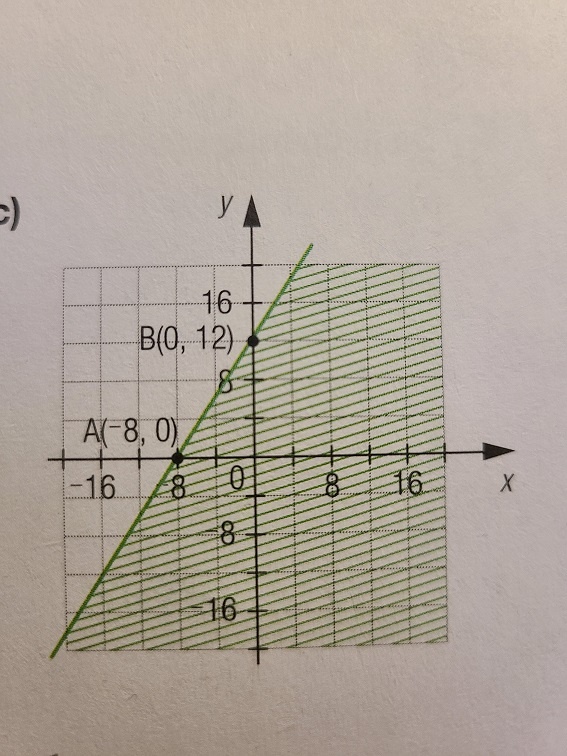
Pour le problème suivant:
Je n'arrive pas à savoir où est-ce que j'ai merdé.
En temps normal, ont doit faire y-y/x-x mais à chaque fois que je fais le calcul, je n'arrive jamais à la bonne réponse.
Est-ce qu'il y a quelqu'un qui pourrait me l'expliquer pour voir où est-ce que je me trompe?
Merci








Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour Sam!
Si je comprends bien, tu as de la difficulté à traduire en inéquation le plan présenté, c'est bien ça?
En premier lieu, on doit identifier l'équation de la droite frontière sous la force \(y = m\times x + b\) en utilisant les coordonnées des points fournis sur le graphique, c'est-à-dire \( (-8, 0)\) et \( (0, 12 )\).
La pente \(m\) se trouve avec l'équation suivante:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
où \( y_1\), \(y_2\), \(x_1\) et \(x_2\) proviennent des points donnés sur le graphique.
Pour ton problème, la pente est:
$$ m = \frac{12 - 0}{0 + 8} = 1.5 $$
L'ordonnée à l'origine se trouve en utilisant la pente \(m\) trouvé à l'étape précédente et en remplaçant dans l'équation les coordonnées \(x\) et \(y\) d'un des deux points fournis. Pour ton problème, l'ordonnée à l'origine est donnée directement dans le graphique (\( 0, 12\)).
Nous avons donc l'équation de la droite frontière suivante:
$$ y = 1.5 \times x + 12 $$
Ensuite, on remarque sur le graphique que la droite frontière est pleine (et non en pointiller). Ceci nous permet de statuer que le symbole de l'inéquation sera \(\leq\) ou \(\geq\).
Pour connaître quel symbole utiliser dans l'inéquation, je te suggère de prendre un point au hasard sur le graphique qui est dans l'ensemble solution et en déduire le sens du symbole.
Pour ton problème, il est possible de procéder de la façon suivante:
Prenons le point \((0, 0)\) qui est dans l'ensemble solution. En remplaçant ce point dans l'équation de la droite frontière, on a:
$$ 0 = 1.5 \times 0 + 12$$
donc,
$$ 0 = 12 $$
Puisque \( 0 < 12\), le symbole à utiliser dans l'inéquation est \( \leq \):
$$ y \leq 1.5x + 12 $$
Pour plus d'information concernant les inéquations, je t'invite à consulter cette page sur notre site web:
J'espère avoir répondu à ta question. Si tu as d'autres interrogations, n'hésite pas à les poser dans la zone d'entraide! :)
Charles
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!