Postsecondaire • 1a
(Calcul différentiel, sciences de la nature)
Bonjour,
J'ai de la difficulté à trouver le domaine de la fonction suivante, car mes valeurs exclues (qui seront mes candidats à l'étude pour la, ou les, discontinuité.s) ne sont pas bonnes. Le domaine est supposé être:
IR\{7π/6 ; 11π/6}
Mais je trouve:
IR\{5π/3}
Ça fait un bout que je n'ai pas touché au cercle trigonométrique...pouvez-vous m'aider? Merci!
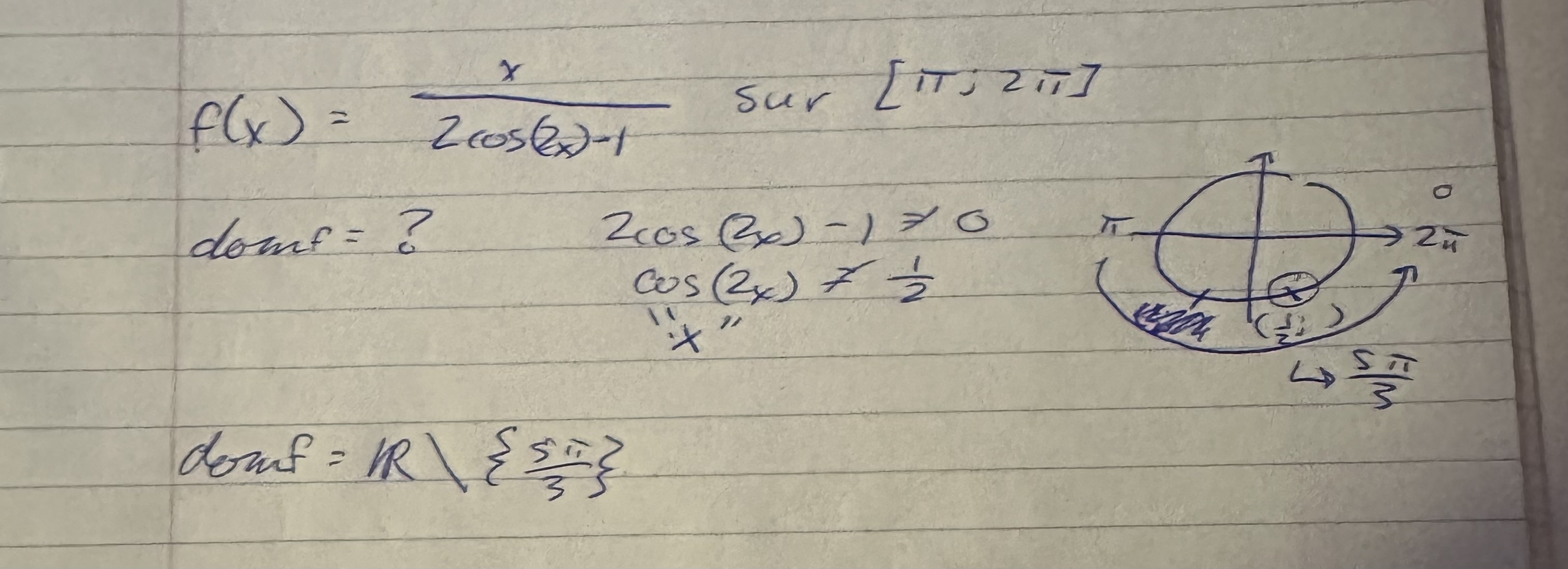






Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Le domaine doit être tel que π ≤ x ≤ 2π donc 2π ≤ x ≤ 4π
on doit aussi s'assurer que 2cos(2x) -1 ≠ 0
cos(2x) ≠ 1/2
dans le cercle trigonométrique cela signifie que 2x doit être différent de π/3 + k2π et 5π/3 + k2π, pour tenir compte de la période de 2π (note que pour 2π/3 et 4π/3 le cosinus est de -1/2)
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce qui revient à un x qui doit être différent de π/6 + kπ et 5π/6 + kπ
dans l'intervalle [π,2π] il y a π/6 + π = 7π/6 et 5π/6 + π = 11π/6 qu'on doit exclure
donc le domaine de la fonction est [π, 2π] \ {7π/6, 11π/6}
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!