Bonjour,
A) Je n'arrive pas à comprendre l'ensemble solution de l'inéquation de la fonction sinus. J'ai obtenu les même zéros de la fonction que le corrigé, mais après, le corrigé utilise "4π +4πn" au lieu de "zéro+4πn". Voici les images:
Le problème:
La solution:
B) L'une de mes grandes confusions théoriques concerne la méthodologie pour trouver les zéros et résoudre l'inéquation. En fait, mon enseignant avait dit d'utiliser "sinx" et "sin(π-x)". Toutefois, je comprend pas comment écrire les équations avec ceux-ci et avec quelle partie de l'équation initiale, particulièrement quand aucune équivalence n'est trouvé dans le cercle trigonométrique.
Par exemple, dans ce cas, (-√2/2) est dans le cercle trigonométrique, et on peut le remplacer par (π/4). Mais considérons un cas où le nombre est introuvable dans le cercle. Comment procéder? Pouvez-vous svp m'expliquer cette méthode?
J'ai vraiment besoind de votre aide pour me préparer pour mon examen :_(
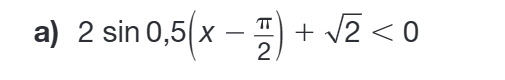
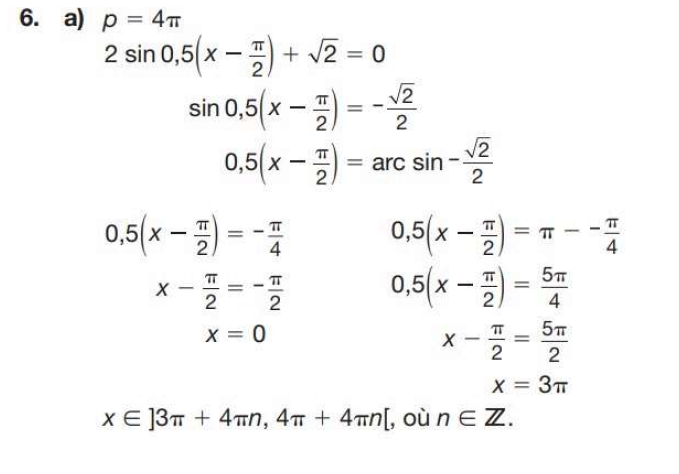






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Pour ta première question, tu aurais pu écrire "zéro+4πn" au lieu de "4π +4πn", c'est la même chose! ;) On a simplement pris le point équivalent du cycle suivant en additionnant la période de 4π à 0. En d'autres mots, tu aurais pu écrire n'importe laquelle de ces expressions : "0+4πn", "4π +4πn", "8π +4πn", "12π +4πn", etc.
Le corrigé a probablement choisi "4π +"0+4πn"" au lieu de "0+4πn" afin de mieux voir le premier terme, parce que si on choisit 0, on devrait écrire alors "4πn" seulement (l'addition du 0 est inutile), ce qui pourrait mélanger des élèves.
Concernant ta seconde question, si le point n'est pas sur le cercle trigonométrique, tu dois simplement utiliser ta calculatrice! En fait, même si le point est sur le cercle trigonométrique, tu peux tout de même utiliser ta calculatrice, mais s'il s'agit d'un examen, il se peut que tu n'y aies pas le droit pour voir justement si tu es capable d'utiliser le cercle trigonométrique.
Par exemple, pour ton exercice 6 a), on obtient aussi -π/4 à la calculatrice :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Attention, il faut t'assurer d'être en radians et non en degrés! De plus, dépendamment des calculatrices, il se peut que la réponse ne soit pas exacte et soit arrondie comme ci-dessus, c'est pourquoi dans ce cas-là le cercle trigonométrique est une meilleure option.
Si le point n'est pas sur le cercle, alors tu es obligé d'utiliser une calculatrice (donc ce n'est pas le genre d'exercice qu'on te donnerait dans un examen où la calculatrice est interdite). Par exemple, si on cherche le sinus de π/5, on s'attendrait à obtenir une réponse entre 1/2 (0,5) et √2/2 (0,707), car le point est environ ici :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puisque le point n'est pas sur le cercle, on utilise la calculatrice et on obtient :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce qui est bien entre 1/2 (0,5) et √2/2 (0,707) comme on l'avait prévu.
J'espère que c'est plus clair pour toi! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!