Bon matin!
Je voudrais encore clarifier certaines doutes qui persistent sur la fonction sinus en trigonométrie.
Merci à SoleilPhilosophe d'avoir répondu à ma question, mais j'ai encore plusieurs doutes qui ne sont pas claires après l'explication :_(
Je peux attendre plusieurs heures, ça me dérange pas, mais svp est-ce que Mme Katia K peut me répondre💖
D'abord, je voulais revenir à ma question précédante sur un exercice impliquant une équation sinus de deuxième degré.
D'abord, j'avais trouvé 4 solutions possibles (avant d'ajouter la période fois n) pour x qui donnent une ordonnée de 0 dans le cercle trigonométrique.
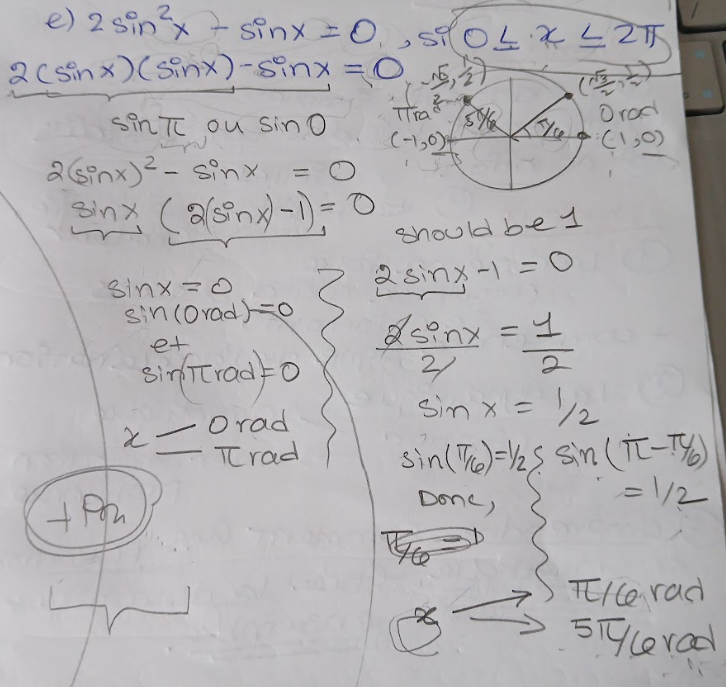
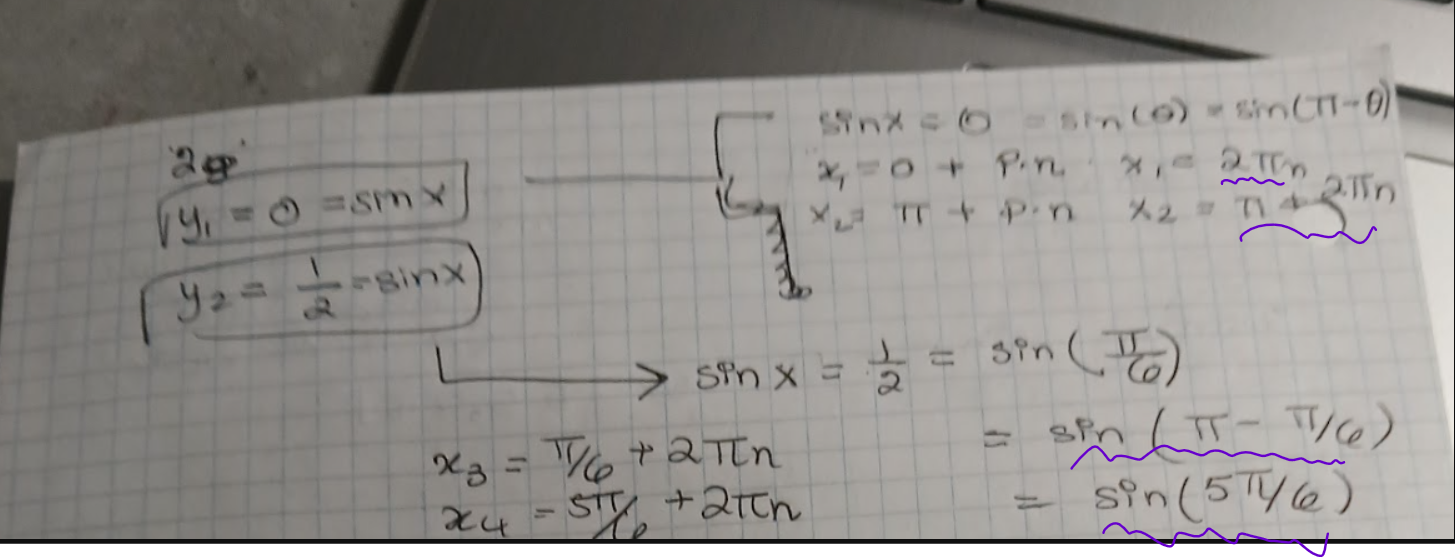
Ainsi, j'ai trouvé les 4 valeurs de x suivantes 0, pi, pi/6 et 5pi/6.
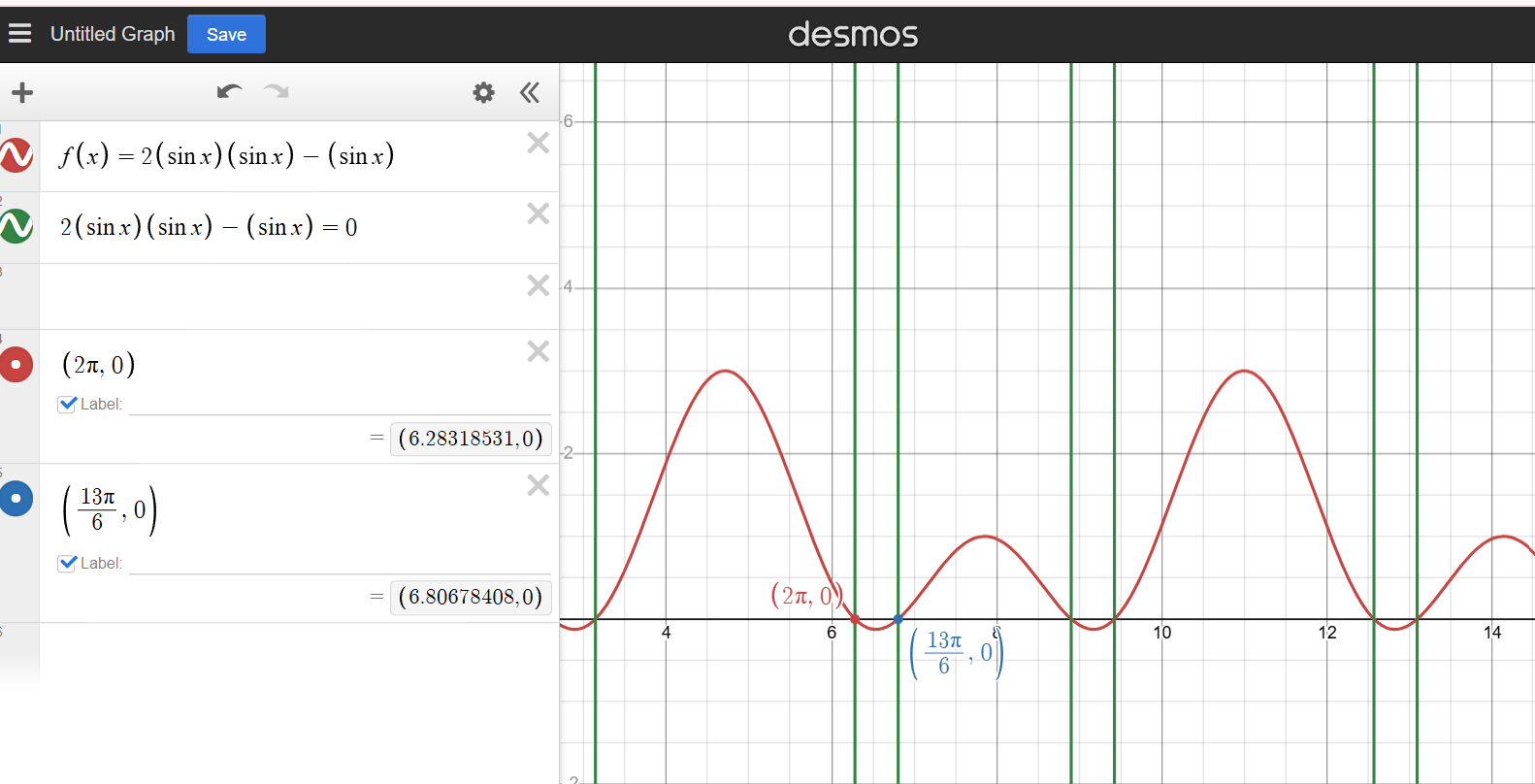
J'ai essayé de tracer la règle avec Desmos et en regardant le graphique, une chose me confondait: Après un certain intervalle (en vert), j'ai toujours deux types de solutions. Par exemple, je vous ai affiché deux des points en exemple. Or, moi j'ai trouvé 4 zéros, alors que dans le graphique, il n'y en a que 2 zéros qui se répètent!
Sinon, comment est-ce que je passe de cette forme de second degré à la forme f(x) = a sin (b(x-h))+k ? Je vous demande cela, car sans la valeur de b, je ne peux pas calculer la période. SVP c'est la plus mêlante que jamais.
Voici une photo du corrigé:
De plus, une autre confusion c'est que pourquoi est-ce qu'il faut ajouter p fois n après les valeurs de x? Dans ce graphique, je n'arrive pas à délimiter la période et surtout interpréter le sens de mes solutions une fois que j'ajoute p x n ? Je n'arrive pas à le voir, car cette équation est un peu différente et elle a des amplitudes différentes + longueurs d'ondes différentes.
Aussi, que signifie concrètement la contrainte de x? Pourquoi ils ont donné un intervalle, je n'en comprends absolument rien et qu'est-ce que cela veut dire?
Svp j'ai vraiment vraiment besoin d'aide, car je sais que je vais avoir des exercices comme ça lors de l'évaluation. C'est un peu poussé :_(
Merci et j'attends de vos explications détaillées :D
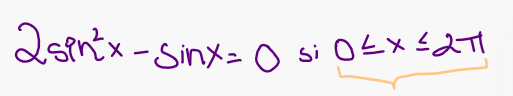






Bonjour CannebergeEnthousiaste9454,
Katia n'étant pas disponible actuellement, je me permets de te donner d'autres détails. Elle précisera probablement les choses lorsqu'elle sera disponible.
Les 4 solutions que tu avais trouvées sont les bonnes. À l'intérieur d'un cycle (d'une période), il n'y a effectivement que ces 4 solutions.
Lorsque tu dis qu'il n'y a que deux zéros qui se répètent, ce n'est pas faux, mais ces zéros sont insuffisants pour donner la solution, il faut donner les 4 que tu as trouvés. On peut justifier cela de deux façons :
1 - l'intervalle de répétition de ces deux zéros est irrégulier, il est donc impossible de généraliser en ajoutant n fois la période. Par exemple, l'écart entre 2𝜋 et 17𝜋/6 est de 5𝜋/6 alors que l'écart entre 17𝜋/6 et 4𝜋 est de 7𝜋/6. L'écart étant irrégulier, on ne peut pas trouver de périodicité si on ne conserve que 2 zéros.
2 - Lorsqu'on cherche les zéros d'une fonction périodique, on doit trouver tous les zéros qui se trouvent dans un cycle. Je t'ai mis en évidence une période (bleutée). On peut voir qu'il y a bien 4 zéros dans une période (le zéro du début compte aussi pour le zéro de la fin de la période que j'ai mise en évidence).
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Donc tu dois conserver les 4 zéros que tu as trouvés même si, visuellement, il semblerait qu'il n'y en ait que 2.
Par ailleurs, comme Léa-Kim l'a précisé, il est impossible de réécrire ta fonction sous la forme d'une équation sinusoïdale du premier degré. Ce genre de problème est difficile car c'est la somme de deux fonctions périodiques. Lorsque les deux fonctions ont la même période, comme c'est le cas ici, la période globale est la même. Lorsque les deux fonctions périodiques additionnées n'ont pas la même période (je ne crois pas qu'on va te donner ça...) la période résultante est le plus petit commun multiple des 2 périodes. Tu peux t'amuser à tracer des fonctions sur Desmos pour voir ce que ça donne...
Sur un graphique on peut trouver la période en raisonnant ainsi : un cycle, c'est la plus petite partie du graphique qui te permet de refaire le graphique au complet uniquement avec des copier-coller. Tu peux voir sur mon schéma que si tu copies-colles la section bleutée tu pourrais recomposer le graphique.
Pour ce qui est de la contrainte sur x : c'est simplement que la question ne veut pas avoir toutes les réponses; on ne demande que les réponses dans cet intervalle. Et dans cet intervalle il n'y a que 5 valeurs de x qui arrivent à zéro.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Allo CannebergeEnthousiaste9454,
Merci pour ta question!
Madame Katia ne travaille pas aujourd'hui. Je vais te répondre au meilleure de mes capacités.
Il y a bel et bien 4 zéros dans une fonction sinusoïdale du deuxième degré. Si on regarde desmos, il y a les deux avant la plus haute vagues et deux après. Ce ne sont pas les même qui se répètent. Dans certains cas, il se peut que oui, mais ce n'est pas la généralité.
Tu ne peux pas passé du deuxième degré au premier degré. Ce n'est pas la même fonction. C'est un peu comme si je te demande de passer d'une parabole à une droite.
Finalement, l'intervalle de x sert à cibler une partie du graphique. C'est pour réduire l'intervalle du graphique. On l'utilise lorsque le problème écrit à des restrictions. Par exemple, on voudrait évaluer un phénomène pendant 8 heures.
J'espère que ça t'aidera! N'hésite pas à revenir au besoin!
Lea-Kim
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!