Zone d’entraide

AluminiumJaune4681

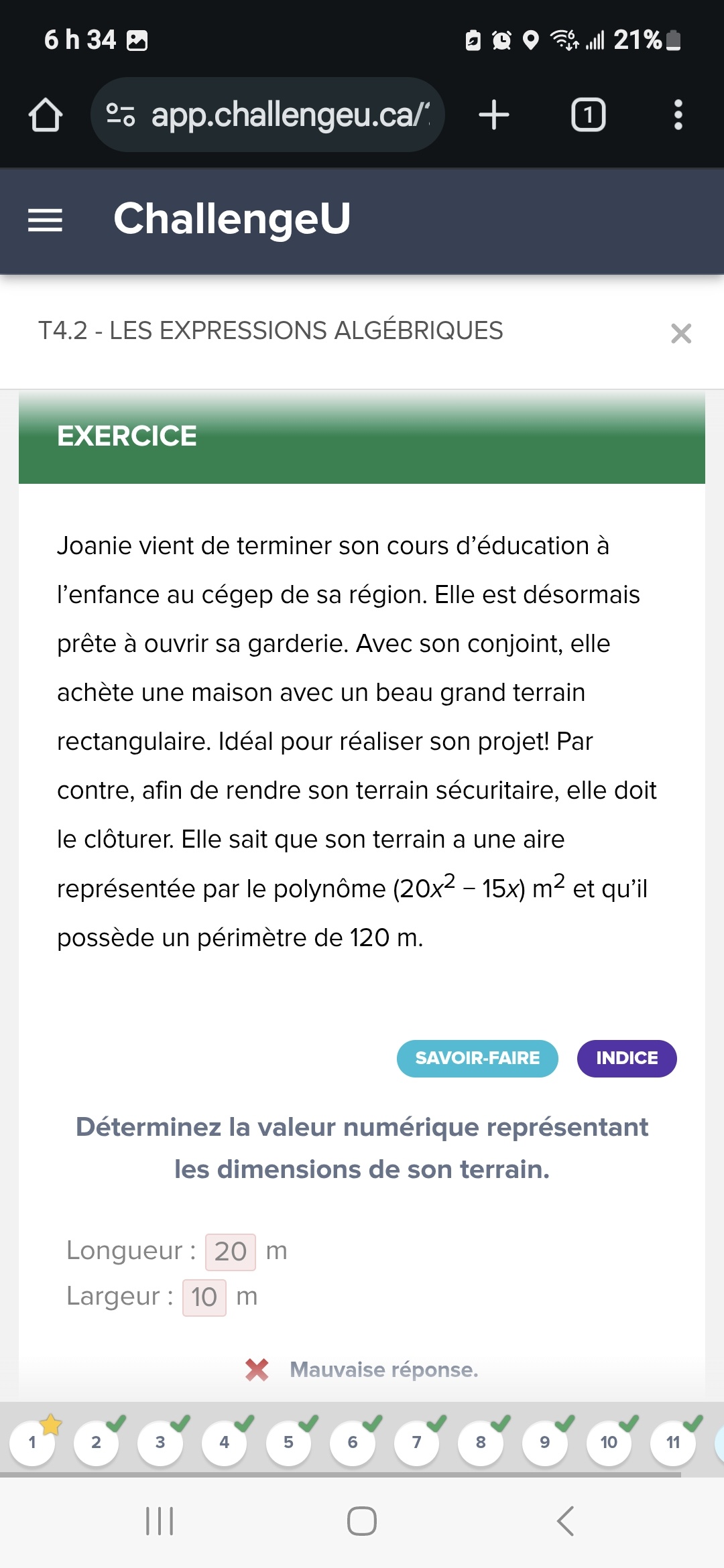
J'ai réussi à trouver le pgdc après qu'est ce que je fais? Merci

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Katia K

Salut!

Tu dois factoriser l'expression algébrique représentant l'aire afin d'avoir deux facteurs : l'un sera la longueur et l'autre la largeur du rectangle.

Ceci n'est pas bon :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

car on tu multiplies 5x² par (4x-3), on obtiendrait 20x³-15x², et non notre expression initiale 20x²-15.

Pour factoriser 20x²-15, tu dois trouver le plus grand facteur commun.

Tu as trouvé que 5 est le PGCD entre 20 et 15, c'est bien!

Maintenant, si on analyse les variables, le premier terme, 20x², possède la variable x², tandis que le deuxième terme, -15, ne possède aucune variable.

Donc, le plus grand facteur commun de 20x² et -15 est 5, et non 5x².

Tu auras donc ceci une fois que tu factorises l'expression algébrique :

$$20x²-15$$

$$5(4x²-3)$$

Donc, une des mesures de côté du rectangle est de 5 m, et l'autre est de (4x²-3) m.

Si tu avais eu l'expression algébrique suivante : 20x²-15x, alors le plus grand facteur commun aurait été 5x, car il y a la variable x dans les deux termes, et on doit toujours garder le plus petit exposant! L'expression factorisée serait donc 5x(4x-3), et les mesures de côtés auraient alors été 5x et 4x-3. Je te conseille de consulter la fiche suivante, elle t'aidera à mieux comprendre : La mise en évidence simple | Secondaire | Alloprof

Si on revient à ton exercice, maintenant que tu as les expressions algébriques pour chaque côté, soit 5 m et (4x²-3) m, tu peux utiliser le fait que le périmètre est de 120 m pour poser cette équation :

Périmètre = 2*longueur + 2*largeur

$$120=2(5) + 2(4x^2-3)$$

Il ne te reste plus qu'à la résoudre pour trouver x!

Avec x, tu pourras déterminer la valeur numérique des mesures de côtés :)

J'espère que c'est plus clair pour toi! Si tu n'es toujours pas sûr(e) de bien comprendre quelque chose, reviens nous voir!