Bonjour! J'ai trois petites questions sur des problèmes de CST de 5 reliés aux figures, lignes, et solides équivalents. J'ai un peu de mal à comprendre comment trouver les mesures demandées, donc desindices sur comment les résoudre seraient très appréciés ! Merciii
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.









Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Des solides équivalents ont le même volume, des figures équivalentes ont la même aire.
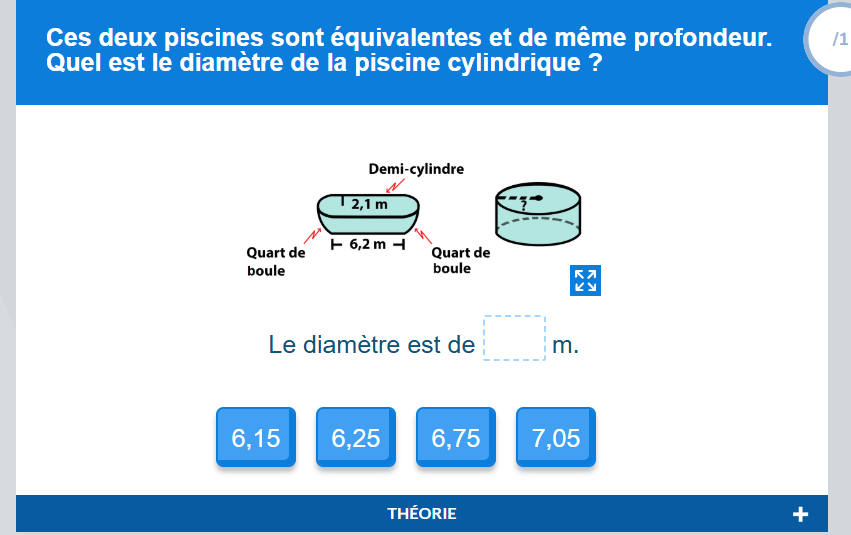
Pour les piscines, tu sais que les volumes sont égaux et que la profondeur ou hauteur h est la même. En égalant les volumes des piscines, tu pourras trouver la hauteur.
Pour t'aider avec les volumes de différents solides, va voir
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/l-aire-et-le-volume-des-solides-m1243
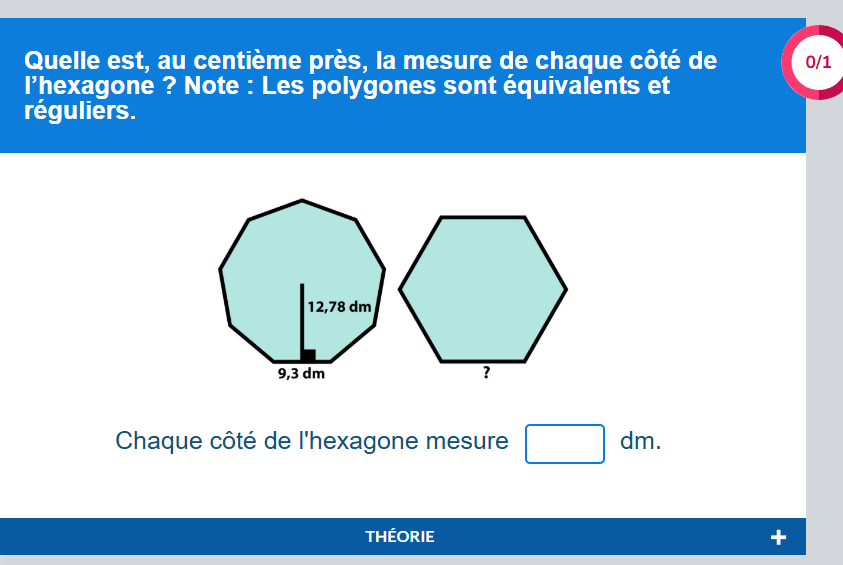
Pour la mesure d'un côté c de l'hexagone, comme l'hexagone et l'octogone sont équivalents, leurs aires sont égales. En égalant les aires tu pourras trouver le côté c manquant.
Pour t'aider avec les aires de différentes figures, va voir
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-perimetre-et-l-aire-des-figures-planes-m1478
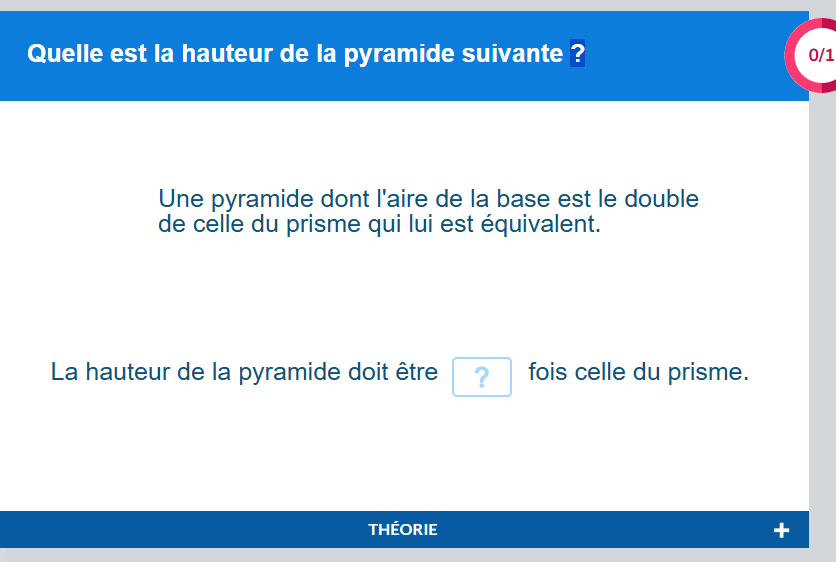
Pour le dernier problème tu as les relations suivantes
notons Ab, l'aire de la base de la pyramide alors on sait que
Ab = 2(aire de la base du prisme)
Ab = 2Abp où Abp est l'aire de la base du prisme (1)
la volume de la pyramide peut être exprimée en fonction de l'aire de sa base et de sa hauteur: c'est Ab x h /3 (2)
comme on nous dit que le prisme est équivalent à la pyramide, cela veut dire que
volume du prisme = volume de la pyramide (3)
par ailleurs le
volume du prisme = aire de la base du prisme x hauteur du prisme = Abp x hp où hp est la hauteur du prisme
en remplaçant par leurs valeurs les expressions en (3) on a
Abp x hp = Ab x h
suivant (1) on peut écrire
(Ab/2) x hp = Ab x h
et je te laisse sur ce dernier indice.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!