Zone d’entraide

OrAutonome2754

Bonsoir,

J'ai une question concernant ce numéro : je n'arrive pas à la bonne réponse est je ne sais pas pourquoi, pouvez-vous svp m'expliquer.

Question : 2 droites perpendiculaires se rencontrent au point (9,2). Si l'abscisse à l'origine d'une des droites est le double de l'abscisse à l'origine de l'autre alors une somme possible de ces abscisses à l'origine est de

A : 17/2

B : 10

C : 51/2

D : 45/2

E : 5

La bonne réponse est la C, mais selon mes calculs je n'arrive pas à cela.

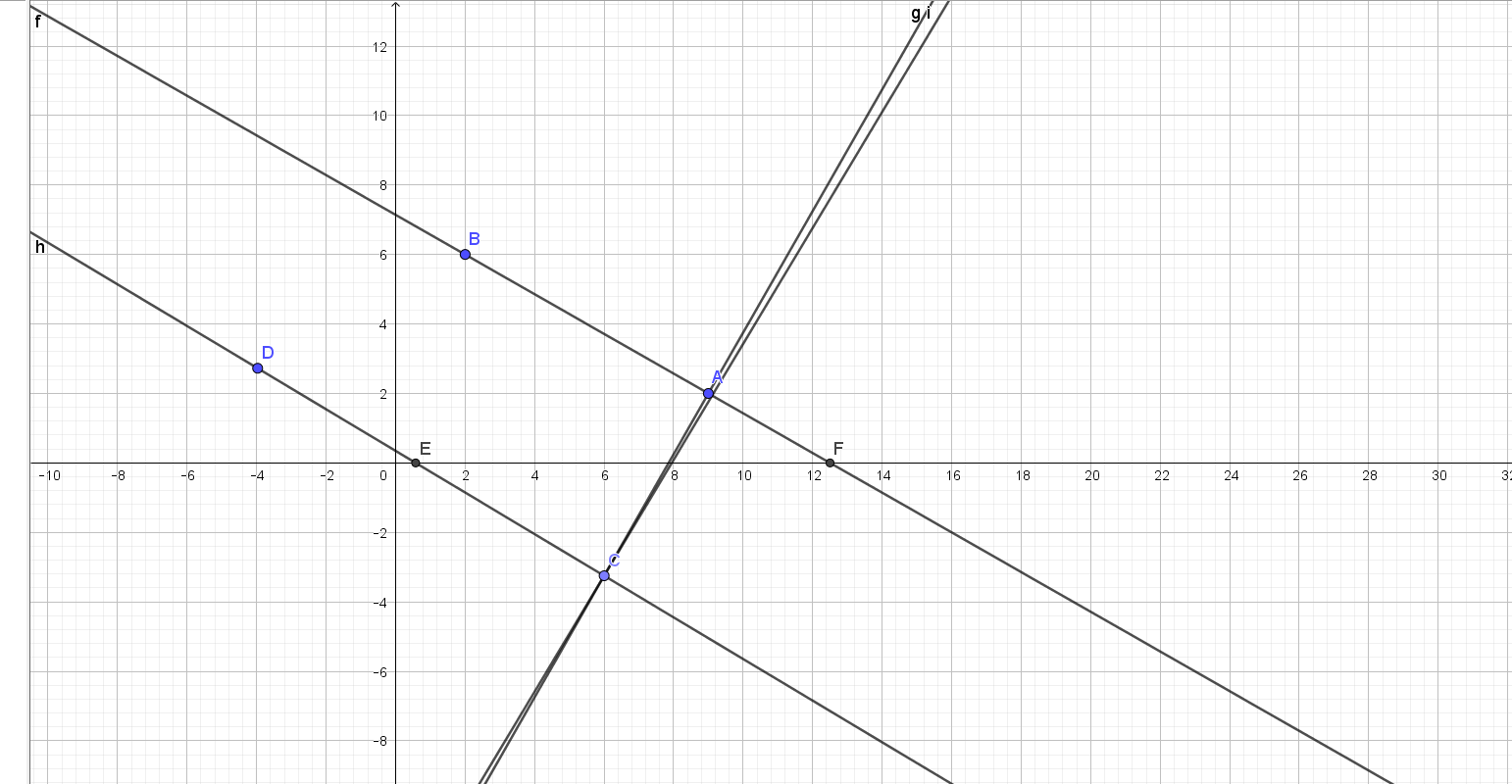
Voici mon graphique

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Merci et bonne soirée! :)

Simon

Salut !

Il y a plusieurs façons de procéder. C'est un bon exercice difficile.

Disons que la pente de la première est \(a\). La pente de la deuxième est \(\displaystyle -\frac{1}{a}\) car les droites sont perpendiculaires.

Disons que l'ordonnée à l'origine de la première est \(b_1\) et l'ordonnée à l'origine de la deuxième est \(b_2\).

Les équations des droites sont de la forme \[y = ax + b_1\] \[y = -\frac{1}{a}x + b_2\]

Sachant que le zéro de l'une est le double de celui de l'autre, on pourrait d'abord poser \[0 = ax + b_1\] \[0 = -\frac{1}{a}(2x) + b_2\]Tu vois ? Le zéro de la première est \(x\), le zéro de la deuxième est \(2x\).

Sachant que les deux droites passent par le point \((9, \, 2)\), on pourrait aussi poser \[2 = 9a + b_1\] \[2 = -\frac{1}{a}(9) + b_2\]

Ça fait beaucoup de variables. Heureusement, on peut isoler \(b_1\) et \(b_2\) dans la deuxième série d'équations : \[2 - 9a = b_1\] \[2 + \frac{9}{a} = b_2\]

On peut ensuite faire de la substitution dans la première série d'équations. Les équations\[0 = ax + b_1\] \[0 = -\frac{1}{a}(2x) + b_2\]deviennent \[0 = ax + 2 - 9a\] \[0 = -\frac{2x}{a} + 2 + \frac{9}{a}\]

Si tu isoles \(a\) dans la première, tu obtiens \[0 = ax + 2 - 9a\] \[9a - ax = 2\] \[(9-x)a = 2\] \[a = \frac{2}{9-x}\]

Si tu isoles \(a\) dans la deuxième, tu obtiens \[0 = -\frac{2x}{a} + 2 + \frac{9}{a}\] \[\frac{2x}{a} - \frac{9}{a} = 2\] \[\frac{2x - 9}{a} = 2\] \[2x - 9 = 2a\] \[\frac{2x - 9}{2} = a\]

Enfin, tu peux poser les deux expressions correspondant à \(a\) égales \[\frac{2}{9-x} = \frac{2x - 9}{2}\]Avec le produit croisé, j'obtiens \[2(2) = (9-x)(2x-9)\]

Tu vas obtenir une trinôme du deuxième degré. Tu peux résoudre avec la formule quadratique ou factoriser avec la méthode somme-produit. Tu obtiendras deux valeurs pour \(x\). Puisqu'on veut la somme des zéros, tu devras calculer \[x + 2x \ = \ ?\] Y a-t-il une valeur qui correspond à un des choix de réponses ?

Bon travail !