Zone d’entraide

HibouResponsable7939

Bonjour,

Je fais une situation problème en devoir et il y a quelque chose que je ne comprend pas (voir les photos). comment puis-je trouver une solution qui respect les délais demandé ET le nombre de grains maximum a ranger?

Merci d'avance

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Anthony B

Salut HibouResponsable7939,

Merci pour ta question!😊

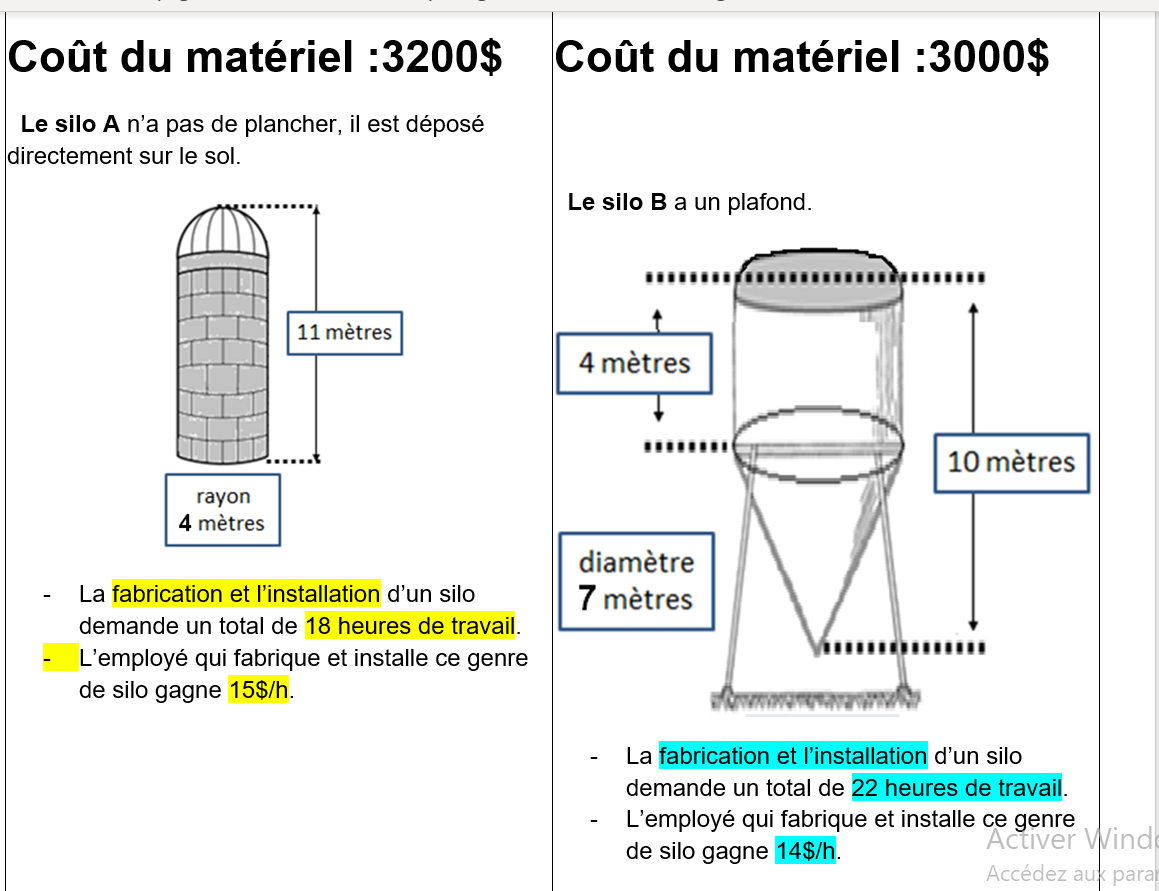
Dans ce problème, Arthur a vendu 5 silos du modèle A et 4 silos modèle B, cependant il n'est pas capable de fournir tous ces silos-là. Ta tâche est donc de faire une nouvelle commande qui respecte les contraintes qui te sont données.

Je vais t'aider à les sortir. Tu as accès à 130h pour la fabrication et l'installation et tu peux utiliser 8 camions pour le transport, c'est-à-dire que tu peux vendre un maximum de 8 silos.

Ensuite, l'agriculteur peut entreposer un maximum de 3350m3 de grain, donc le volume total de tes silos ne doit pas dépasser ce volume.

Ton but est donc de proposer à ton oncle une nouvelle commande qui minimise le temps et les couts. Également, tu dois mentionner le profit réalisé sur la vente.

Donc tu dois trouver quelle combinaison de silos respecte les conditions et minimise le temps et les couts.

J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions! 😉

Anthony B.