Zone d’entraide

missgirl

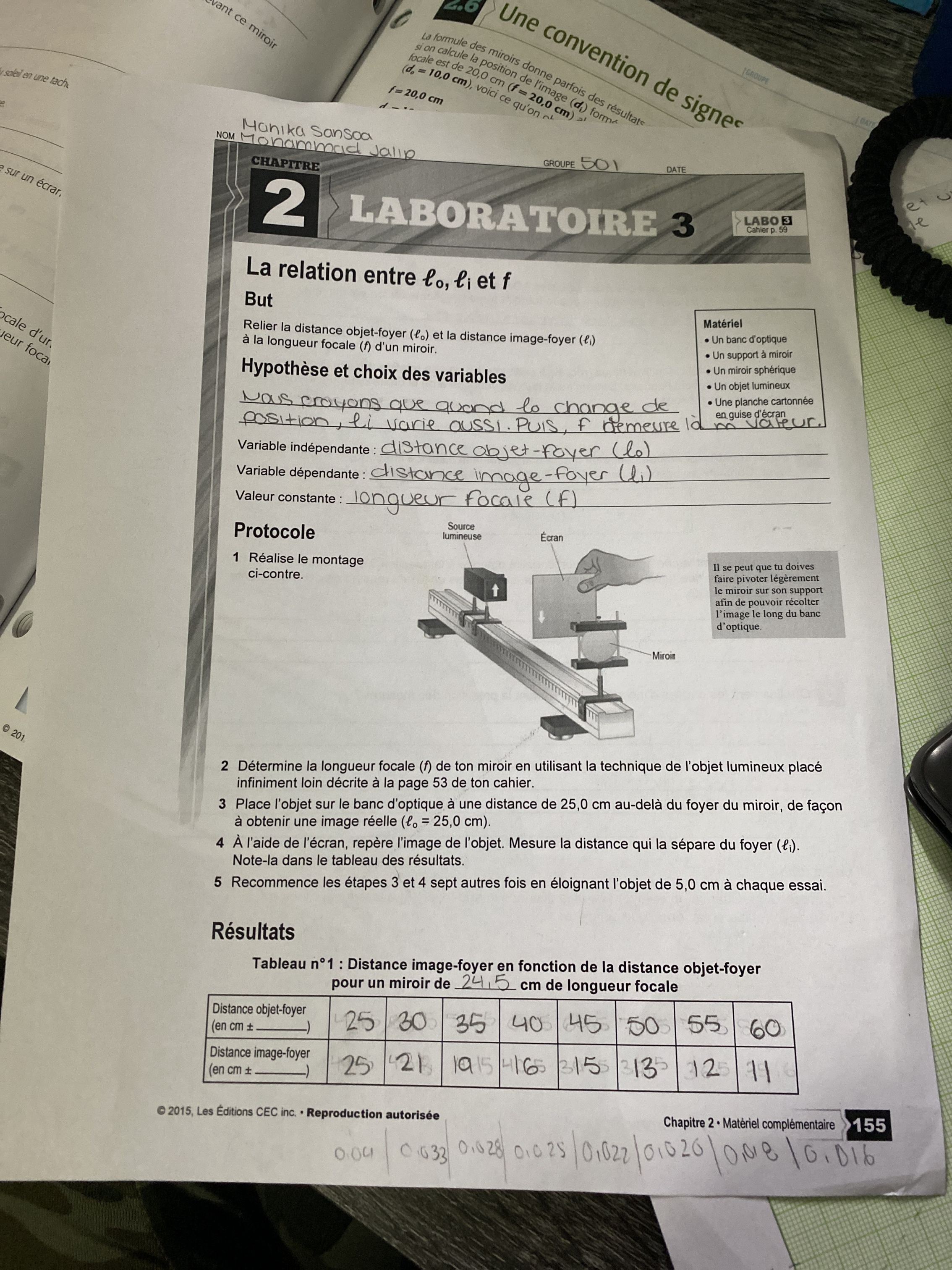
Je ne comprend pas le #3. Je crois que mon taux de variation est mauvais. Cependant chaque fois que je le calcule, il me donne le même.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Louis-Philippe B

Salut à toi !

Merci pour ta question!

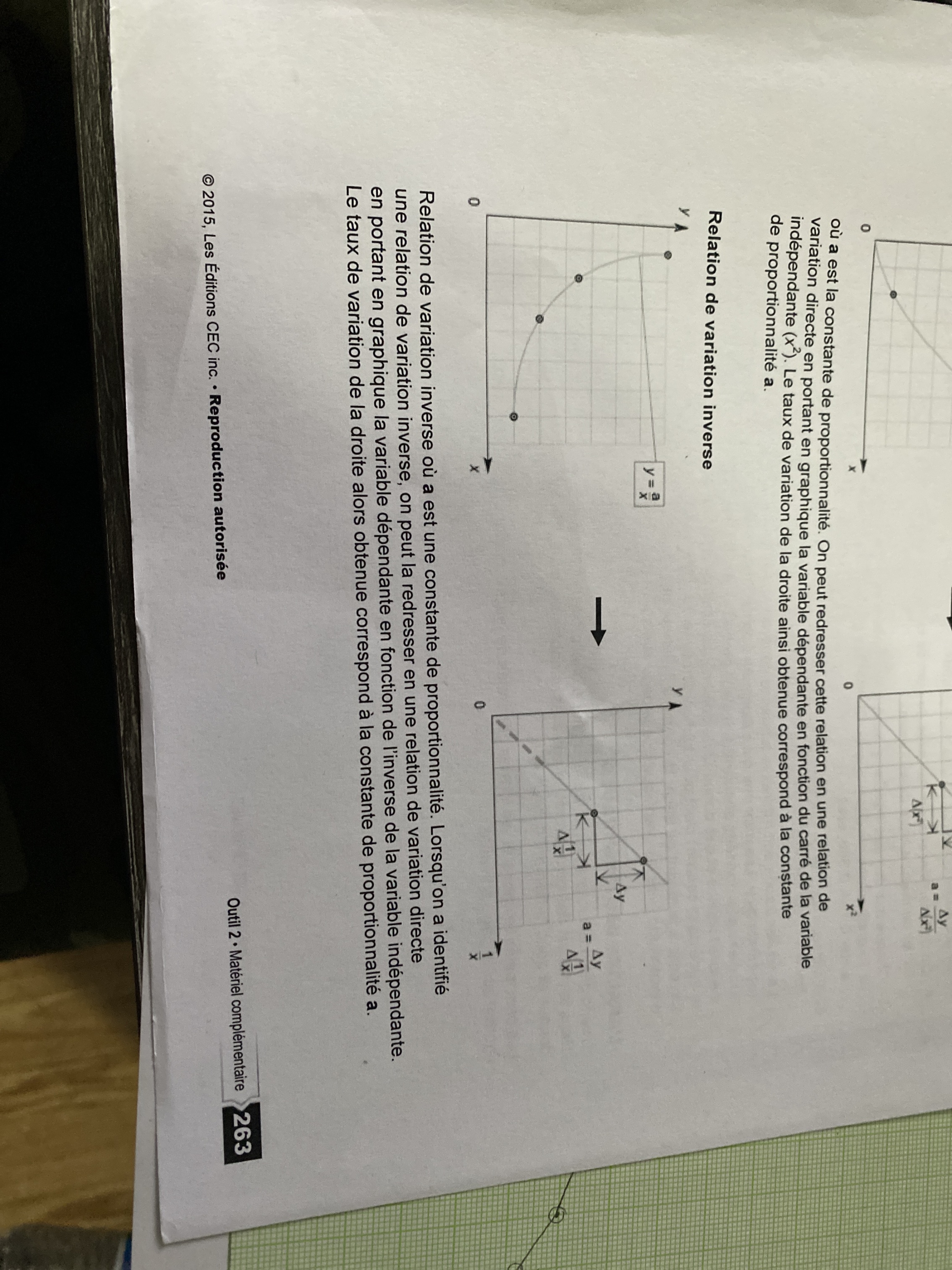
Pour répondre à la question, il faut d'abord « redresser » la courbe, comme il est indiqué dans la troisième image que tu as envoyé.

Pour ce faire, il faut trouver l'inverse de la première et la dernière valeur de la variable dépendante (si on fait les calculs à la main). Dans ce cas-ci, il s'agit de la distance objet-foyer.

Première valeur :

$$\frac{1}{25cm}=0,04c{m}^{-1}$$

Dernière valeur :

$$\frac{1}{60cm}=0,01\bar{6}c{m}^{-1}$$

Puis, on trouve le taux de variation (attention : comme on a trouvé l'inverse des valeurs des variables dépendantes, x1 devient x2, y1 devient y2 et vice versa) :

$$a=\frac{∆y}{∆x}=\frac{y_2-y_1}{x_2-x_1}=\frac{25-11}{0,04-0,01\bar{6}}\approx 600$$

Par curiosité, j'ai refait le graphique sur Excel pour confirmer ma réponse. Effectivement, le logiciel obtient une valeur assez proche (puisqu'il tient compte de tous les points) :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voilà!

N'hésite pas si tu as d'autres questions! :)

Jojo

1/x = 1/0.002 = 500

-2/ 500= -0.004