Secondaire 4 • 2a
Bonjour!
Dans ce problème, lorsque je fais la formule quadratique, le x est inexistant. Est-ce que ça veut dire qu’il appartient automatiquement aux réels ou le x pourrait appartenir à un ensemble vide? Dans le fond, comment je fais pour savoir si l’inéquation est toujours vraie ou inexistante/toujours fausse? Dans le corrigé, mon prof a dessiné la parabole dans le 4e quadrant, mais je n’ai jamais non plus compris comment savoir dans quel quadrant je dois dessiner la parabole lorsqu’elle n’a pas de x.
Merci!
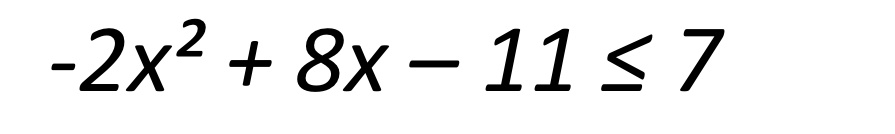






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour!
En fait, si tu la place comme une équation au départ, tu peux t'assurer d'avoir 0, 1 ou 2 valeurs en utilisant le calcule racine de (b²-4ac) quand tu as mis ton trinôme égale à 0.
C'est en fait ce que tu retrouves dans la racine du discriminant. Si ta racine est négative, c'est que ta parabole ne coupe pas l'axe des x, si tu as obtenu 0 à ton discriminant, c'est que ton sommet est sur l'axe des x et si tu as un positif, c'est que tu auras 2 réponses possibles.
Pour l'inéquation, tu peux la poser ensuite avec le même raisonnement.
Bonjour!
Si la formule quadratique ne donne pas de solution pour x, cela signifie que l'équation n'a pas de solution réelle. Cela ne signifie pas nécessairement que x appartient à un ensemble
vide, car il est possible que l'équation ait des solutions complexes.
Pour savoir si l'inéquation est toujours vraie ou toujours fausse, vous pouvez utiliser différentes méthodes en fonction de l'inéquation. Par exemple, si l'inéquation est de la forme
ax^2 + bx + c > 0, vous pouvez étudier le signe du discriminant (b^2 - 4ac) pour déterminer si la parabole s'ouvre vers le haut ou vers le bas, et donc si l'inéquation est toujours
vraie ou toujours fausse.
Pour dessiner la parabole, vous pouvez utiliser les informations que vous avez sur le signe du coefficient a et du discriminant. Si a est positif, la parabole s'ouvre vers le haut,
et si a est négatif, elle s'ouvre vers le bas. Si le discriminant est positif, la parabole coupe l'axe des x en deux points, et si le discriminant est négatif, la parabole ne coupe
pas l'axe des x.
J'espère que cela vous aide!
Dans le fond,si tu a utiliser la forme quadratique,tu devrais voir que la dans le discriminant tu as un chiffre négatif,or c'est impossible d'avoir racine carré d'un nombre négatif.Et donc la fonction est fuasse.C'est aussi simple il ne faut pas chercher plus que ça ,si le discriminant est négatif alors ce n'est même pas une fonction.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!