Postsecondaire • 2a
Bonjour, cela fait longtemps que je n’ai pas posé de questions, mais aujourd’hui je suis revenu de nouveau. Pouvez m’aider dans ce problème de limite? Je ne sais pas si ce que j’ai fait est bon. Si tel est le cas, comment continuer?
D’ailleurs, merci beaucoup de votre aide que vous m’aviez apporté par le passé que ça soit pour moi ou les autres élèves à travers la province.
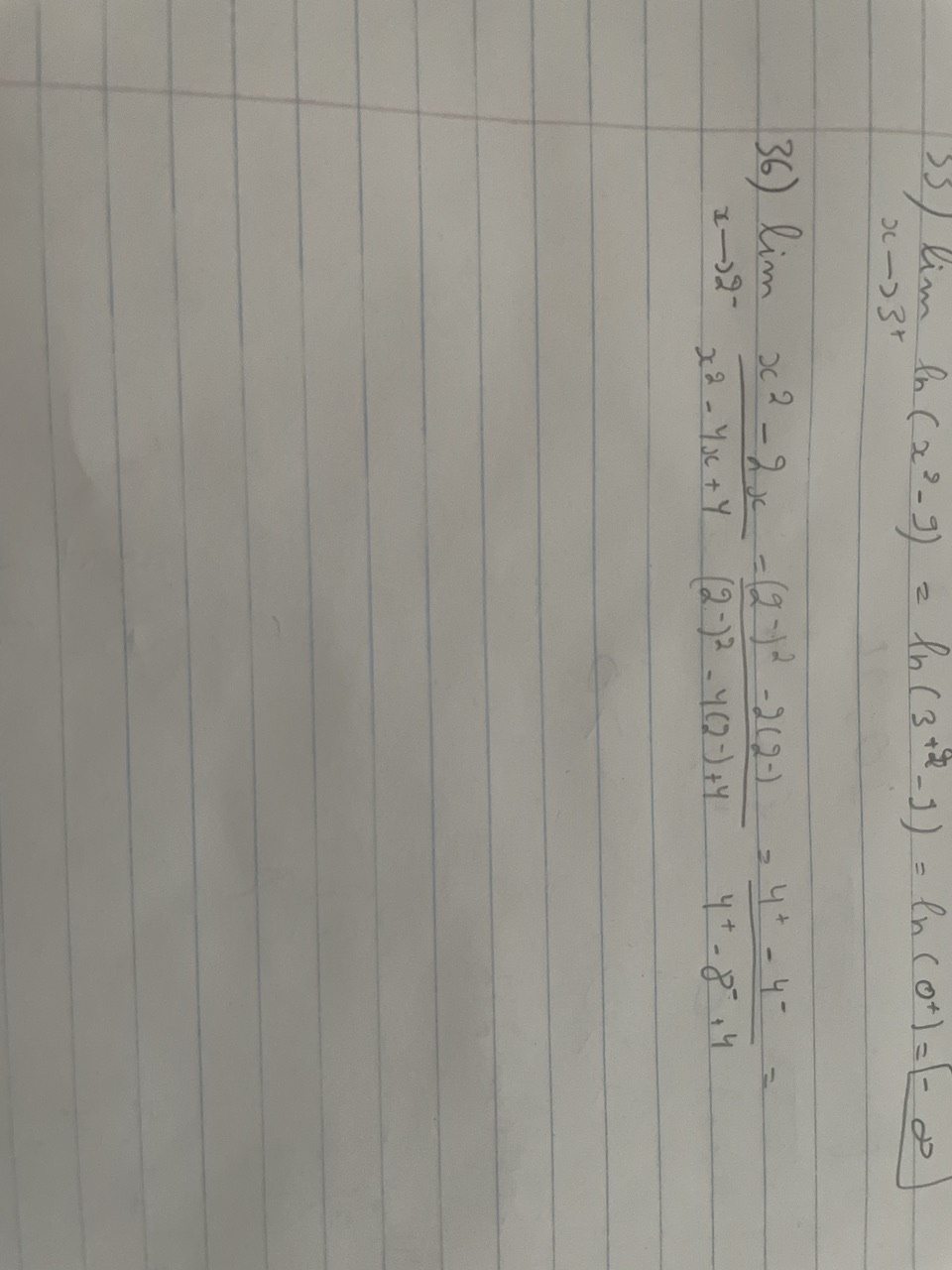






xx-4x+4=(x-2)(x-2) carre parfait
et pas (x-2)(x+2) différence de deux carres
lim (xx-2x)/(xx-4x+4) quand x tend vers 2 par valeurs négatives
on sait que la fonction en question n'est pas définie en 2,
el la limite et de la forme 0/0 indéterminée
tu remarques que xx-2x=x(x-2)
xx-4x+4 est un carre parfait de la forme a-b au carre
xx-4x+4=(x-2)(x-2)
f(x)=(xx-2x)/(xx-4x+4) pour tout x diffèrent de 2
f(x)=(x-2)x/(x-2)(x-2), pour tout x diffèrent de 2
on simplifie le (x-2)
f(x)= x/(x-2) pour tout x diffèrent de 2
maintenant lim f(x) x tend vers 2 par valeurs négatives, elle est de la forme 2/0 c'est +l'infini ou -l'infini
comme x-2 est négatif comme x tend vers 2 par valeurs inferieures donc x-2 tend vers un zéro négatif
et le quotient tend vers -l'infini
La conclusion on commence la simplification et on écrit f(x) sous une forme simplifiée, puis on passe aux limites.
Ce cas se présente tout le temps quand on a le quotient de deux polynômes quand il y a des racines r1, r2... ou zéros communs au numérateur et au dénominateur, on peut diviser autant de fois les deux par (x-r1)(x-r2).... et simplifier l'écriture de la fraction rationnelle.
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Quand tu as une limite à déterminer, commence par voir si tu peux simplifier ton expression.
Ici la factorisation facilite le problème.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Note que comme x tend vers 2 par le côté négatif sur l'axe des x, x est toujours un peu moins que 2 et donc (x - 2) est toujours négatif bien que de plus en plus près de 0, d'où la conclusion.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!