Zone d’entraide

Lili

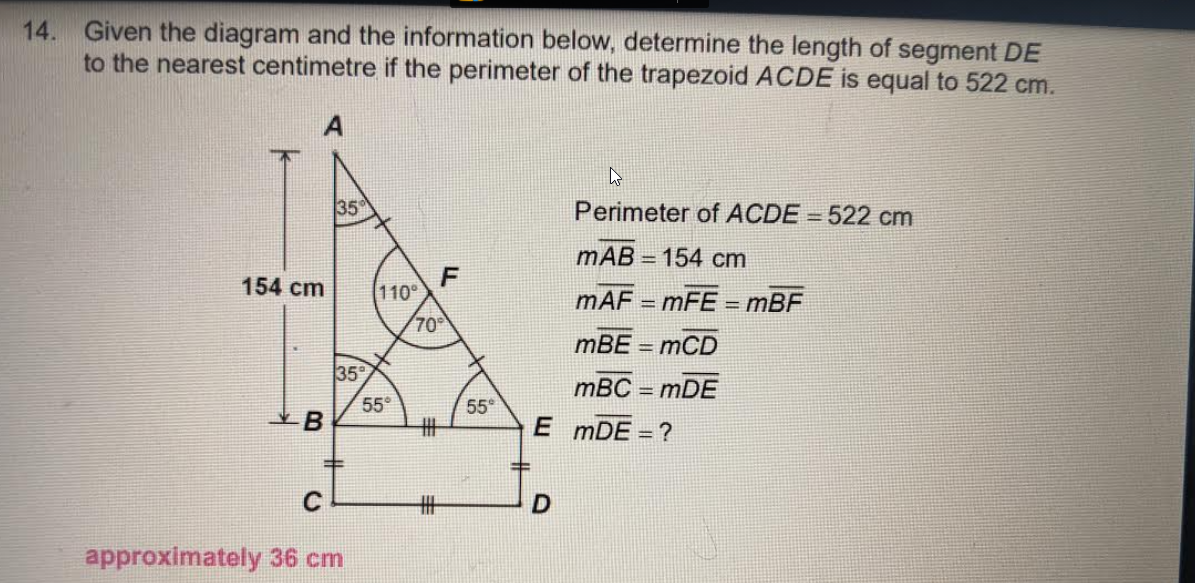
Allo, je ne comprends pas comment arriver à la bonne réponse... je commence par faire un Sin35=154/hyp --> hyp AE = 268.53.

Ensuite AF=FE=BF donc ils ont tous 134.3cm

Ensuite loi des sinus pour trouver BE:

134.3(BF)/sin55 = BE/sin70 --> donc BE = 154.14

Quand j'additionne le tout pour périmètre 154+154.14+268.53, je dépasse le 522 du périmètre total... je ne comprends pas où je me trompe. Vous pouvez m'aider?? merci

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Laura A

Bonjour bonjour !

Merci de faire appel à nos services.

La mesure de segment AE se calcule comme suit:

$$ cosA = \frac{154}{AE} = cos35 = \frac{154}{AE} $$

Donc,

$$ segment AE= 154 \div cos35 = 187.99 ou 188 $$

Ensuite, tu dois diviser cette mesure par 2 pour trouvé les mesures des cotés AF, FE et BF.

Par la suite, calcule le segment BE en utilisant la loi de sin ou tan, sans oublier tan = sinx / cosx. Donc, comme suit:

$$ sin35 = \frac{BE}{188} or \frac{sin35}{cos35}=\frac{BE}{154} $$

Le segment BE est égal au segment CD, le périmètre du trapèze est 522 cm, et BC = ED. Avec ces informations, tu peux établir une équation qui définit le périmètre du trapèze et trouver BC et ED en les dénotant comme \( x \) et isoler pour trouver celle-ci.

Pour t'aider, l'équation du périmètre sera:

$$ 522 = 154+188 + CD + 2x $$

À toi d'appliquer le tout. N'hésite pas à repasser si tu as d'autres questions. :)

Laura

AvocatTenace6777

bonjour,

Erreur → Sin35=154/hyp

P.S. Laura a eu une bonne idée de calculer mBE avec sinus ou tangente dans le triangle ABE.