Secondaire 2 • 2a
Bonjour à tous,
Pendant mon cours de Math mon prof a mis une énigme que je n'ai jamais résolu et qu'il n'ait jamais expliqué le raisonnement ou la raison. Voici l’énigme:
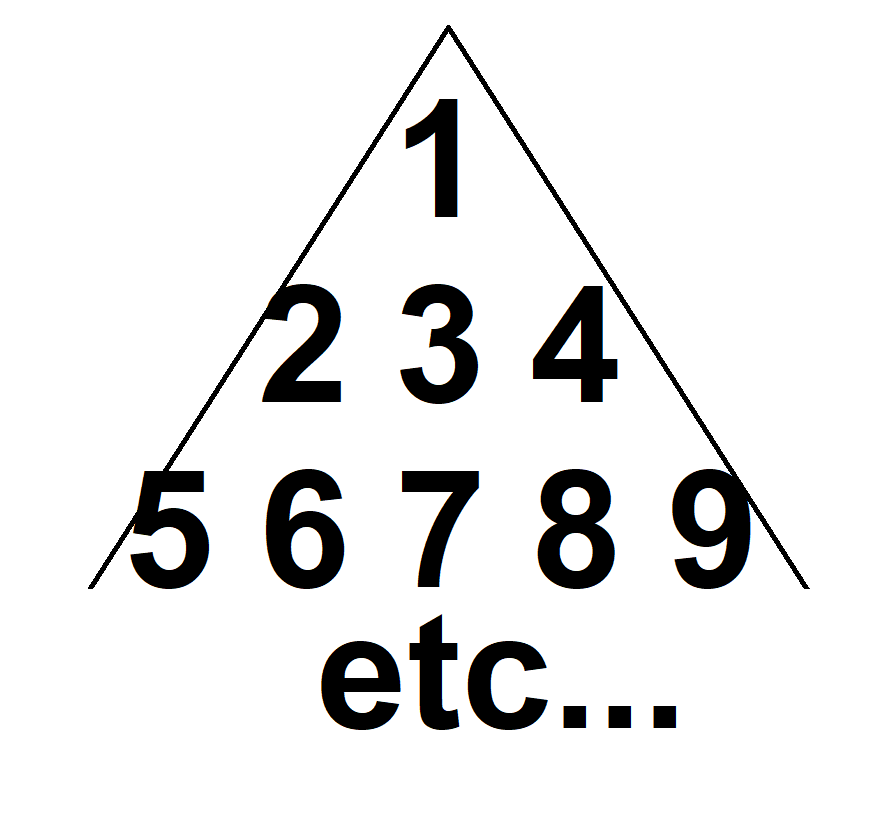
Rogadien demeure dans un immense bloc appartement égyptien. Ce grand immeuble a la forme d'une pyramide* et les appartements sont numérotés de la manière présenté dans l'image en pièce jointe.
La nuit dernière, sont voisin du dessus écoutait du Nickelback très fort et cela agaça profondemment Rogadien; Rogadien veut aller le voir, mais il ne sait pas le numéro de l'appartement de son voisin d'en haut immédiat.
Si Rogadien habite le 2019, quel est le numéro de l'appartement de son voisin du dessus?
Quelqu'un peut me dire comment résoudre ce problème? Merci beaucoup 😊!






Bonjour AvocatPhilosophe4295.
Merci d'avoir utilisé la zone d'entraide pour ta question.
Comme tu peux le voir, les trois nombres sur la ligne de droite sont des carrés parfaits. Les carrés parfaits forment une suite logique. 0, 1, 4, 9, 16. +1, +3, +5, +7. Comme les additions dans la suite représentent le nombre d'appartements par étage, chaque nombre à droite sera un carré parfait.
Il faut commencer par trouver les deux carrés parfaits les plus près de 2019. Par essais-erreurs, on trouve 1936 (44^2) et 2025 (45^2).
2025 est une chambre à droite de 1936, donc 2024 est en-dessous de 1936.
Finalement, pour se rendre au 2019, il faut se tasser de 5 chambres à gauche à 2024. Il faut donc faire la même chose à 1936, donc 1936-5=1931. Rogadien devra se rendre à l'appartement 1931.
J'espère t'avoir aidé.
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
À l'étage n, il y a
∑(2(i-1) + 1) une sommation de i = 1 à n
(pour quelques sommes importantes voir http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomDemo.htm)
= 2 ∑i - n = 2 ( n (n+1)/2 ) - n = n²
S'il habite au 2019 il est au n = 45 ème étage et a 44 étages au dessus
2019 - (2 (45 -1)) = 2019 - 2 · 44 = 1931
si je n'ai pas fait d'erreur :-)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!