Postsecondaire • 2a
Salut!
J'ai une question par rapport à un exercice de dérivation implicite en calcul différentiel.
L'exercice demande de trouver la dérivée de xe^y=y*sin(x).
Je me demande juste pourquoi dans la partie de droite, la dérivée de y*sin(x) donne : y'sin(x)+ycos(x). De mon côté, en le faisant, j'obtenais y*y'*sin(x)+y*cos(x), donc j'avais un y de plus. Je l'ai mis parce que normalement, la dérivée de y, c'est y*y', non?
(J'ai joint ma démarche)
Merci!
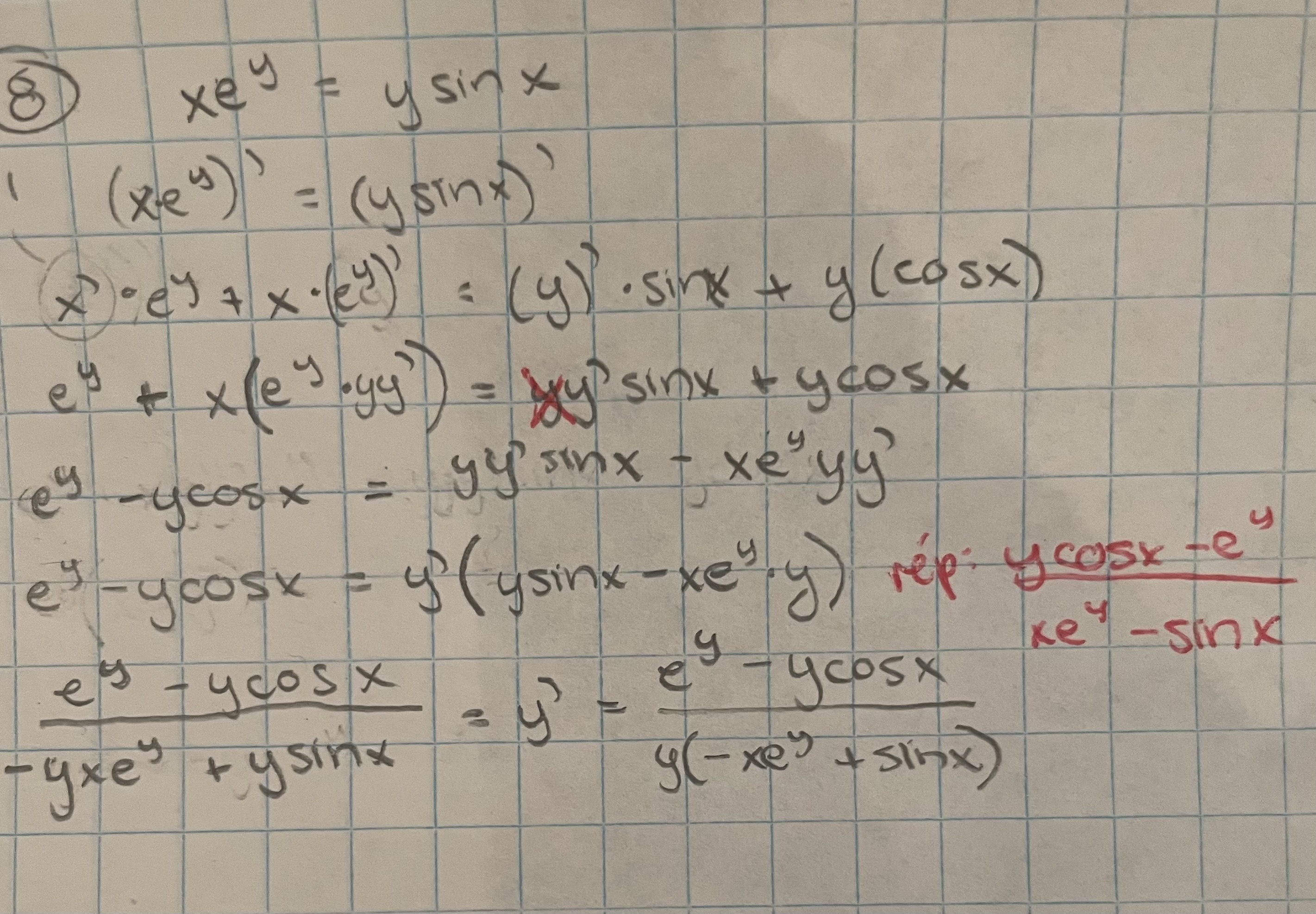






☺
On a y=f(x) alors la dérivée de y peut s'écrire y' ou f'(x), mais pas yy' ni f(x)f'(x).
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
La dérivée de y par rapport à x que (y' ou dy/dx): c'est ce que tu cherches
J'ai corrigé tes erreurs, tu as besoin de revoir les règles de dérivation.
https://w1.cirrelt.ca/~errico/table_derivees.pdf
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!