Zone d’entraide

CannebergeEnthousiaste9454

Bonjour!

1) J'aimerais savoir et comprendre comment on est arrivé à la forme factorisée suivante (la démonstration et la passage de cette forme à l'autre): a(x-x1)(x-x2) = 0 à partir du trinôme ax2+bx+c = 0? Est-ce que nous devons employer la complétion du carré? Si oui, comment?

Voici un passage de mon cahier:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

2) Pour l'exercice ci-contre, je ne comprends pas comment procéder... Il me semble que mes résultats ne sont pas dans le format a(x-x1)(x-x2) et n'est pas les mêmes que le corrigé.

Je vous encercle les numéros. Pouvez-vous me montrer un exemple de démarche pour les numéros en rose (sutout le c) et m'expliquer où est mon erreur?

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici le corrigé:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Merci beaucoup de votre compréhension :D

ZincDelta7925

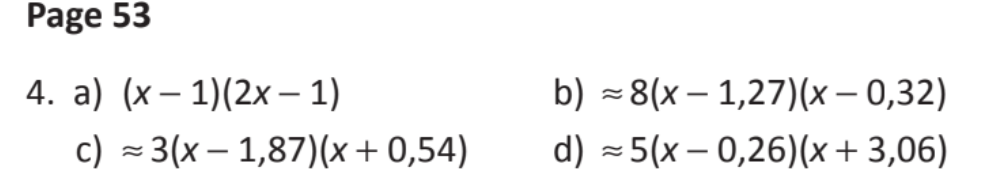
Tu as tout fait

pour le c) et d) tu es arrivé à la différence de deux carres

tu considères 13/9=(racine(13/9))²

et tu fais la différence de deux carres

a(b²-c²)=a(b-c)(b+c)

3((x-2/3)²-13/9)=

3((x-2/3)²-(racine(13/9))²)=

3 ((x-2/3)-racine(13/9)) (x-2/3)+racine(13/9))

3 (x-(2/3+racine(13/9))) (x-(2/3-racine(13/9)))

2/3+racine(13/9)=1.87

(2/3-racine(13/9)=-0.54

3 (x-1.87) (x-(-0.54)=3 (x-1.87) (x+0.54)

de même pour

5((x+7/5)²-69/25)

voici la démonstration de la factorisation d'un trinôme

https://www.youtube.com/watch?v=WWNvRoBhpMg

Mélissa S

Salut :D

Oui, l'énoncé t'indique de factoriser à l'aide de la complétion du carré.

Pour réviser la procédure, c'est par ici.

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-completion-du-carre-m1386

En voici un aperçu.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Vers la fin de ta démarche, tu dois obtenir une DC, puis la factoriser à nouveau.

Au c), lorsque tu ajoutes et soustrais la même valeur, il s'agit de (b/2)^2.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ici, ton b est -4/3, alors, la valeur à ajouter, puis à soustraire est (b/2)^2, soit (-4/3/2)^2, qui devient (-4/6)^2, puis -4/6*-4/6 = 16/36, qui est réduite à 4/9. Il est écrit 4/6 dans ta démarche, une de tes erreurs se situe à ce niveau.

Tu peux confirmer avec le corrigé en classe au retour pour vérifier le reste de la démarche, ou réessayer avec cette nouvelle valeur. :) À bientôt sur la Zone! :D