Zone d’entraide

GrillonNoble3915

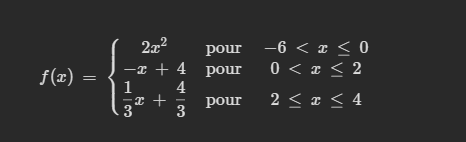
Ce sont les règles d'une fonction définie par parties

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Si f(x) = 4, c'est quoi les valeurs ?

J'ai vraiment tout essayé. Ca me donne environ:

-1.41, 0 et 2.67

J'aimerais aussi comprendre la démarche à suivre mais je dois vraiment débloquer la suite du cahier.

ZincDelta7925

Tu dois résoudre f(x)=4 pour chacun des intervalles de définition de ta fonction.

La question qui se pose est :

Existe-t-il un x dans ] -6, 0] pour lequel f(x)=4

dans ce cas, on résout 2x²=4 ce qui donne

x²-2=0 ou (x+racine(2))(x-racine(2))=0, c'est-à-dire x=-racine(2) ou x=racine(2)

comme -2 appartient à ] -6, 0] x=-racine(2) est solution

racine(2) n'est pas solution parce que racine(2) n'appartient pas à ] -6, 0] .

Existe-t-il un x dans ] 0, 2] pour lequel f(x)=4

-x+4=4 , -x=0 ,x=0 comme 0 n'appartient pas à ] 0, 2]

x=0 n'est pas solution de l'équation f(x)=4.

Existe-t-il un x dans [ 2, 4] pour lequel f(x)=4

(1/3)x+(4/3)=4

(x+4)/3=4/1 ,

x+4=12, x=8

8 n'appartient pas à [ 2, 4], l'équation n'admet pas de solutions dans l'intervalle [ 2, 4]

conclusion

L'équation f(x)=4 admet une solutions dans l'intervalle de définition de la fonction f soit ] -6, 4]

La solution est x=-racine(2),

S={-racine(2)}

Un graphique peut aider à visualiser les solutions, mais on peut s'en passer par une résolution directe et précise des équations dans chacun des intervalles.

Je t'invite à refaire l'exercice pour chacun des cas f(x)=5/2, f(x)=8, f(x)=2.

Katia K

Salut!

Comme expliqué par FerUpsilon5520, tu peux tracer le graphique de la fonction définie par parties, puis vérifier quelle fonction passe par y = 4. Tu constateras ainsi que la seule sous-fonction possédant une ordonnée de 4 est la première, soit 2x².

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu peux utiliser le logiciel Desmos pour t'aider à tracer le graphique.

Ensuite, tu devras calculer l'abscisse de ce point comme ceci :

$$ 4 =2x^2$$

$$ 2 =x^2$$

$$ x=\sqrt{2}$$

Une autre façon de procéder sans devoir dessiner le graphique serait de calculer y=4 pour chaque sous-fonction de f(x). Puis, tu devras vérifier que l'abscisse obtenue est bien dans l'intervalle où la sous-fonction est définie.

Première sous-fonction :

$$ 4 =2x^2$$

$$ 2 =x^2$$

$$ x=\sqrt{2}≈1,41$$

x=1,41 est bien dans l'intervalle -6 < x ≤ 0.

Deuxième sous-fonction :

$$ 4 =-x+4$$

$$ 4-4 =-x+4-4$$

$$ 0 =-x$$

$$ x=0$$

x=0 n'est pas dans l'intervalle 0 < x ≤ 2 (le 0 est exclu de l'intervalle).

Troisième sous-fonction :

$$ 4 =\frac{1}{3}x+\frac{4}{3}$$

$$ 4 -\frac{4}{3}=\frac{1}{3}x+\frac{4}{3}-\frac{4}{3}$$

$$ \frac{8}{3}=\frac{1}{3}x$$

$$ \frac{8}{3}\times 3=\frac{1}{3}x \times 3$$

$$x=8$$

x = 8 n'est pas dans l'intervalle 2 ≤ x ≤ 4.

Nous obtenons alors la même réponse que la première méthode!

J'espère que c'est plus clair pour toi! :)

FerUpsilon5520

Moi, dessiner le problème, ça m'aide énormément.

Tu devrais faire le graphe, tu réaliserais qu'il n'y a qu'une valeur de x sur les intervalles considérés où f(x)= 4 (et c'est -√2)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.